Слайд 2F(n) = F(n-1) + F(n-2)
В 1202 году вышла книга "Liber Abaci" итальянского

ученого Леона́рдо Пиза́нского (прозв. Фибоначчи), где он описал знаменитое рекуррентное соотношение
F(n) = F(n-1) + F(n-2)
Почему же это соотношение такое известное?
Рассмотрим три задачи.
Слайд 3Задача о кроликах
Пусть в огороженном месте имеется пара кроликов (самка и самец)

в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов.
Сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?
Слайд 4Задача о последовательностях
Требуется подсчитать количество последовательностей длины N , состоящих из 0 и 1,

в которых никакие две единицы не стоят рядом.
Слайд 5Задача о мячике на лесенке
На вершине лесенки, содержащей N ступенек, находится мячик, который начинает

прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну.
Требуется определить число всевозможных "маршрутов" мячика с вершины на землю.
Где встречались эти задачи?
Связь задач динамического программирования и рекуррентных соотношений.
Что общего в этих задачах?
Слайд 6Что общего в этих задачах?
Последовательность Фибоначчи возникает при решении всех этих на

первый взгляд несвязанных задач.
Можно получить это соотношение отдельно для каждой задачи, а можно установить соответствие между решениями этих задач.
Используя эти задачи можно вывести соотношение для вычисления F(n)
Слайд 7РС порядка k.
Опр.1
Рекуррентное соотношение = РС

Слайд 8Решение РС
Опр.2
Решением рекуррентного соотношения называется последовательность при подстановке которой в соотношение получается

тождество.
У одного РС может быть бесконечно много решений.
Для РС порядка К, мы можем первые К-1 элемент задать произвольно.
Слайд 9Простой пример
Назовите какое-нибудь решение РС:
f(n) = 3 * f(n-1)
Назовите:
одно решение;
еще два;
общий вид

решения;
А если f(1) = 7.
А нельзя ли обобщить наше решение на большее число РС?
Слайд 10Общее решение РС
Решение РС порядка К называется общим, если оно зависит от

К произвольных постоянных С1, С2 … СК и путем подбора этих постоянных можно получить любое решение данного РС.
Слайд 13Решение линейных РС с пост. коэф.













 Простые задачи на умножение и деление
Простые задачи на умножение и деление Среднее арифметическое. Задания
Среднее арифметическое. Задания Инварианты. Общее уравнение кривой второго порядка
Инварианты. Общее уравнение кривой второго порядка Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ  Первообразная
Первообразная Строгие и нестрогие неравенства. 8 класс
Строгие и нестрогие неравенства. 8 класс Задачи. Итоговое повторение
Задачи. Итоговое повторение Линейные рекуррентные соотношения и методы их решения
Линейные рекуррентные соотношения и методы их решения Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики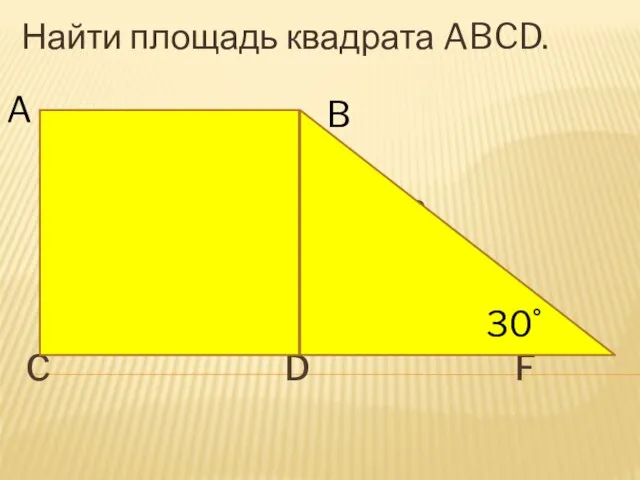 Решение задач. Площадь квадрата
Решение задач. Площадь квадрата Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Таблица сложения
Таблица сложения Асимптоты графика функции
Асимптоты графика функции Случаи вычитания 12 -
Случаи вычитания 12 - Ребусы от тётушки Совы
Ребусы от тётушки Совы Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Вычислить. Задание на лето
Вычислить. Задание на лето Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного День рождения числа Пи
День рождения числа Пи Решение уравнения методом последовательных приближений
Решение уравнения методом последовательных приближений Угол между прямой и плоскостью
Угол между прямой и плоскостью Площа прямокутника
Площа прямокутника Длина. Вес
Длина. Вес Построение сечений в тетраэдре
Построение сечений в тетраэдре Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Функция, ее график и свойства
Функция, ее график и свойства Формулы. Повторение
Формулы. Повторение Теория вероятностей
Теория вероятностей