Bu o deməkdir ki, (2.5) tənliyi (2.1) diferensial
tənliyini bu nöqtədə
tərtib dəqiqliyi ilə aproksimasiya edir. (2.4)
sxemindən fərqli olaraq, (2.5) – münasibətində təzyiqin törəməsi qonşu yarıtam nöqtələr üzrə təyin edilir ki, bu da dayanıqsız sxemlərdən qaçmağa imkan verir. Belə şəbəkə şahmat formalı şəbəkə adlanır. Fərqlər sxeminin yazılışını sadələşdirmək üçün belə bir işarələmə daxil edək:
Bu zaman (2.5) münasibəti indekssiz şəkildə aşağıdakı kimi yazılar
(2.6)
Əvvəllər (2.1) – də biz j – cu və ya
Bu formada qurulan sxemlər aşkar sxemlər adlanır. Belə tənliyə yalnız bir naməlum (j+1) – ci zaman layındakı qiymət
− ci zaman layından istifadə edirdik.
Əgər şəbəkə funksiyalarının j – cu zaman layında qiymətləri -
-daxildir
məlumdursa, onda
qiyməti aşkar şəkildə ifadə olunur, məsələn, (2.6) – dan alınır
ki,
Bu zaman yarıtam nöqtələr şablonunda (şəkil 2.3), analoji olaraq alarıq ki,
Təbii ki, fərqlər tənliyi üçün yuxarı zaman layından istifadə
etmək olar.









 Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Матрицы и действия над ними
Матрицы и действия над ними Разложение многочлена на множители
Разложение многочлена на множители Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Определители второго и третьего порядка
Определители второго и третьего порядка Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Правильные многоугольники
Правильные многоугольники Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Презентация на тему Число и цифра 7 (1 класс)
Презентация на тему Число и цифра 7 (1 класс)  Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс)
Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс) Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников  Время и работа. Связь между величинами
Время и работа. Связь между величинами Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Величины. Объём
Величины. Объём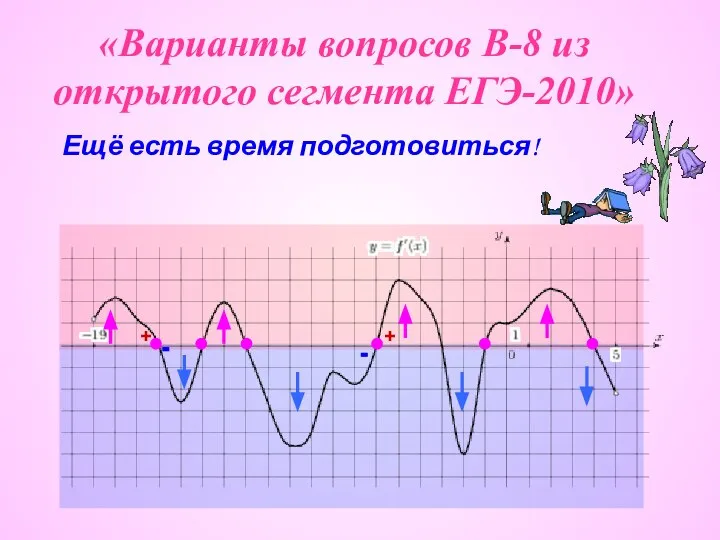 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на кратное сравнение
Задачи на кратное сравнение Entrant
Entrant Решение задач (1 класс)
Решение задач (1 класс) Касательная плоскость к сфере
Касательная плоскость к сфере Наука Метрология
Наука Метрология Задача з піцою
Задача з піцою Тригонометрические уравнения
Тригонометрические уравнения Вычисление логарифмов
Вычисление логарифмов