Слайд 2Девиз урока:
« Дорогу осилит идущий, а математику – мыслящий»

Слайд 3Оценочный лист
Математический диктант - 0 -3 балла
Самостоятельная работа- 0 - 15
Найти ошибку

- 1
Групповая работа- 0 - 5
Мини-тест- 0 - 4
Устный ответ - 1
Слайд 4Математический диктант «Крестики – нолики»
ДА – Х, НЕТ – О
Вопросы:
Логарифмом числа в

по основанию а называется показатель степени, в которую надо возвести а, чтобы получить в
Логарифмическая функция убывает при а<0
Сумма логарифмов чисел равна логарифму суммы чисел
Область определения логарифмической функции - множество положительных чисел
Логарифм 1 равен 1
Логарифм степени равен произведению показателя степени на логарифм основания
Слайд 5Уравнения и неравенства называются логарифмическими, если …
При решении используем свойство …

2 случая: при а … и при а…
Слайд 6Способы решения логарифмических уравнений и неравенств:
1.По определению
2.Метод потенцирования
3.Логарифмирования
4.Введения новой переменной (приведение к

квадратному)
5.Графический
Слайд 7Какими способами решены уравнения?

Слайд 9Использование потенцирования и монотонности функции

Слайд 11Математический софизм
«Найдите ошибку»
2> 3. В чем состоит ошибка этого доказательства?

Слайд 12Указать и исправить ошибки в решении уравнений

Слайд 13log (3x + 2) +log (x + 2) =
=log(2x + 4)
(основание 5)
(3x+

2) + (x + 2) = (2x + 4)
3x + 2 >0, x+ 2>0, 2x + 4>0
3x + 2 +x + 2 =2x + 4 и x>- ,
2x = 0, x= 0.
Ответ: 0
Слайд 14Решить уравнения и неравенство повышенной сложности

Слайд 15
Лист самоконтроля:
1.Свойства логарифмов
2.Свойства логарифмической функции
3.Способы решения уравнений 4.Способы решения неравенств
5.Решение

уравнений и неравенств повышенной степени
Отметить словами знаю или умею
Слайд 16Оцените свою работу.
Самооценка зависит от суммы набранных баллов на всех этапах
Критерии оценок
«5»:

25 и выше баллов
«4»: 15-24
«3»: 10-14















 Применение производной в географии
Применение производной в географии Дискретная математика. Повторение арифметических действий
Дискретная математика. Повторение арифметических действий Трикутники. Елементи трикутника
Трикутники. Елементи трикутника ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Теоремы сложения и умножения вероятностей. Вероятность противоположного события
Теоремы сложения и умножения вероятностей. Вероятность противоположного события Игровой тренажер
Игровой тренажер ОГЭ - 9 класс
ОГЭ - 9 класс Повторение изученного. 1 класс
Повторение изученного. 1 класс Число π. Длина окружности
Число π. Длина окружности Свойства числовых неравенств. 8 класс
Свойства числовых неравенств. 8 класс Метод алгебраического сложения
Метод алгебраического сложения Последовательности. Способы задания и свойства
Последовательности. Способы задания и свойства Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ
Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ  Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Логические основы обработки информации. Алгебра логики
Логические основы обработки информации. Алгебра логики Угол между прямыми
Угол между прямыми Функция. Урок по алгебре в 7 классе
Функция. Урок по алгебре в 7 классе Математика в профессиях
Математика в профессиях Презентация на тему Правильные многогранники
Презентация на тему Правильные многогранники  Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)  Математика в литературе
Математика в литературе Переместительное свойство умножения
Переместительное свойство умножения Скрипт параллелограм
Скрипт параллелограм Презентация на тему Обыкновенные дроби (6 класс)
Презентация на тему Обыкновенные дроби (6 класс) 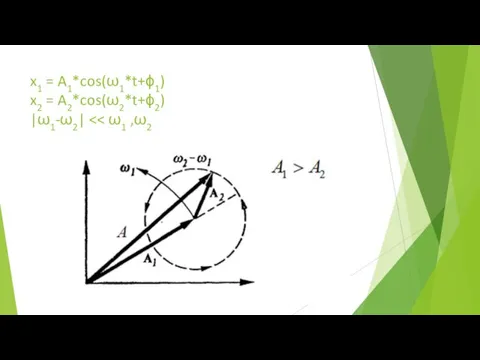 Амплитуда результирующего колебания
Амплитуда результирующего колебания Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Корень степени n
Корень степени n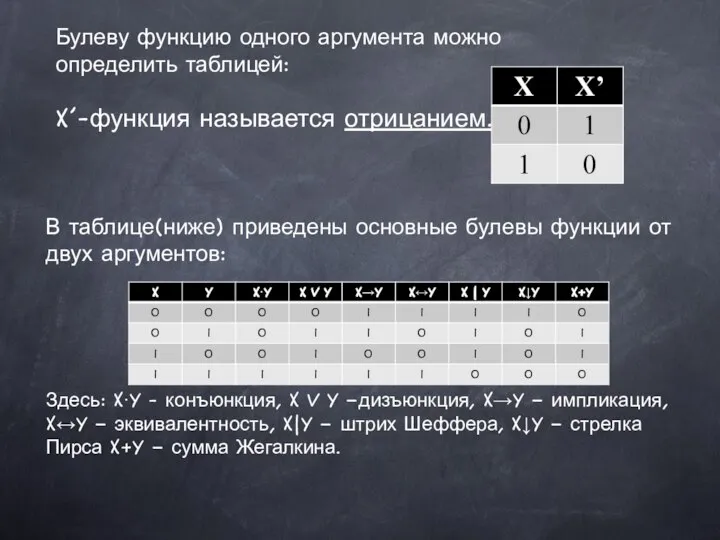 Булевы функции
Булевы функции