Решение задач с параметрами

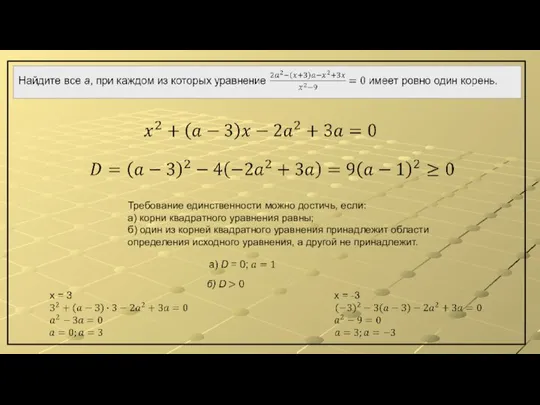
Требование единственности можно достичь, если:
а) корни квадратного уравнения равны;
б) один из корней квадратного уравнения принадлежит области определения исходного уравнения, а другой не принадлежит.

Требование единственности корня исходного уравнения можно достичь, если:
а) уравнение (*) линейное и имеет единственный корень и он положительный;
б) уравнение (*) квадратное и имеет два равных положительных корня;
в) уравнение (*) квадратное и имеет два корня разных знаков;
г) уравнение (*) квадратное, один корень которого равен 0, а другой положительный

Требование единственности корня исходного уравнения можно достичь, если:
а) уравнение (*) линейное и имеет единственный корень и он положительный;
б) уравнение (*) квадратное и имеет два равных положительных корня;
в) уравнение (*) квадратное и имеет два корня разных знаков;
г) уравнение (*) квадратное, один корень которого равен 0, а другой положительный

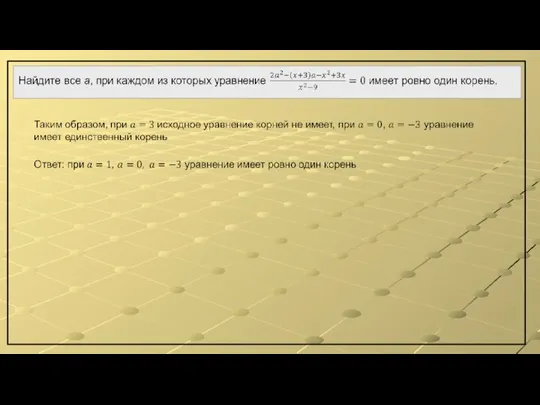
Рассмотрим какие значения должны принимать корни уравнения (*), чтобы выполнялось заданное условие.

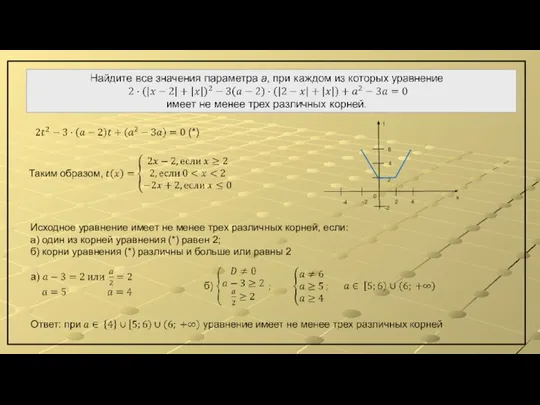
Исходное уравнение имеет не менее трех различных корней, если:
а) один из корней уравнения (*) равен 2;
б) корни уравнения (*) различны и больше или равны 2