Содержание
- 2. Цель урока: обобщить материал по свойствам логарифмов, логарифмической функции; рассмотреть основные методы решения логарифмических уравнений; развивать
- 3. Вспомни и продолжи свойство!
- 4. Вычислите значения выражения
- 5. Вычислить значение выражения
- 6. Определение: Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.
- 9. Решение простейшего логарифмического уравнения основано на применении определения логарифма и решении равносильного уравнения Пример
- 10. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их: если loga f(х)
- 12. Если в уравнении содержатся логарифмы с разными основаниями, то прежде всего следует свести все логарифмы к
- 13. Если в показатели степени содержится логарифм, то обе части уравнения логарифмируют по тому основанию, которое содержится
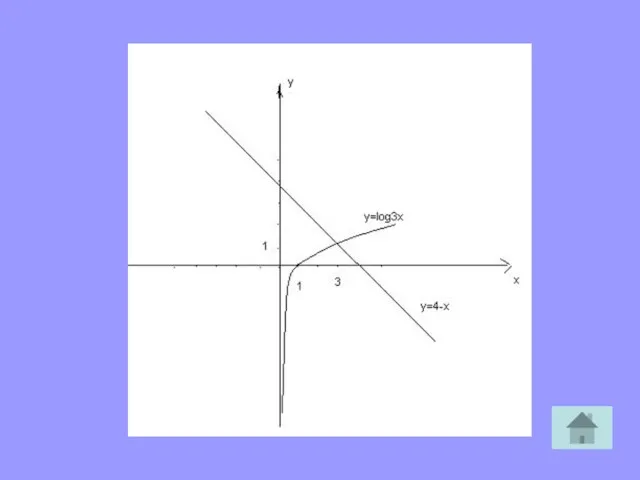
- 14. Для решения ЛУ графическим методом надо построить в одной и той же системе координат графики функций,
- 17. Скачать презентацию






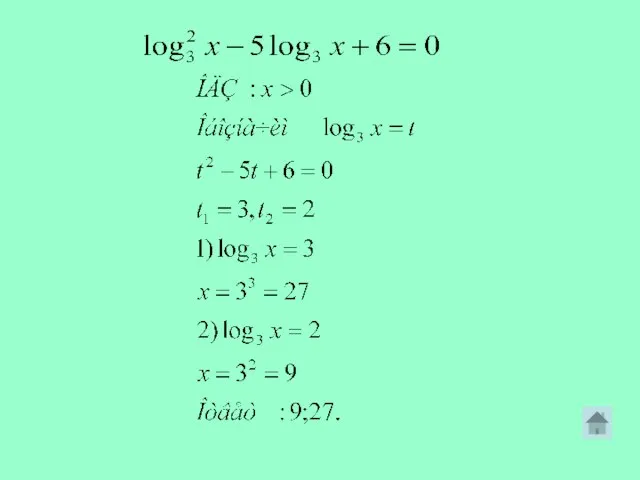






 Kombinatorika
Kombinatorika Задачи на проценты
Задачи на проценты Презентация
Презентация Математические головоломки. Математика вокруг нас
Математические головоломки. Математика вокруг нас Периметр и площадь прямоугольника. Подготовка к контрольной работе
Периметр и площадь прямоугольника. Подготовка к контрольной работе Векторы. Линейные операции над векторами. Разложение вектора по базису
Векторы. Линейные операции над векторами. Разложение вектора по базису Отношение чисел
Отношение чисел Лекция 20
Лекция 20 Домашнее задание по геометрии
Домашнее задание по геометрии Матрицы и действия над ними
Матрицы и действия над ними Итоговая контрольная работа
Итоговая контрольная работа Теорема Пифагора
Теорема Пифагора Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Презентация на тему РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ
Презентация на тему РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ  Основы логистики
Основы логистики Теорема Пифагора и квадратные уравнения
Теорема Пифагора и квадратные уравнения Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Плоскость. Прямая. Луч
Плоскость. Прямая. Луч Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток
Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток Построение графиков функций
Построение графиков функций 1_1_matritsy (1)
1_1_matritsy (1) Юность Великих математиков. 5 класс
Юность Великих математиков. 5 класс Симметрия
Симметрия Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса
Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса Математические ребусы
Математические ребусы Математика без границ. Конкурс
Математика без границ. Конкурс Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Изучить понятия параллельное проектирование и его
Изучить понятия параллельное проектирование и его