Слайд 2Таблица производных
Производные степенной функции.
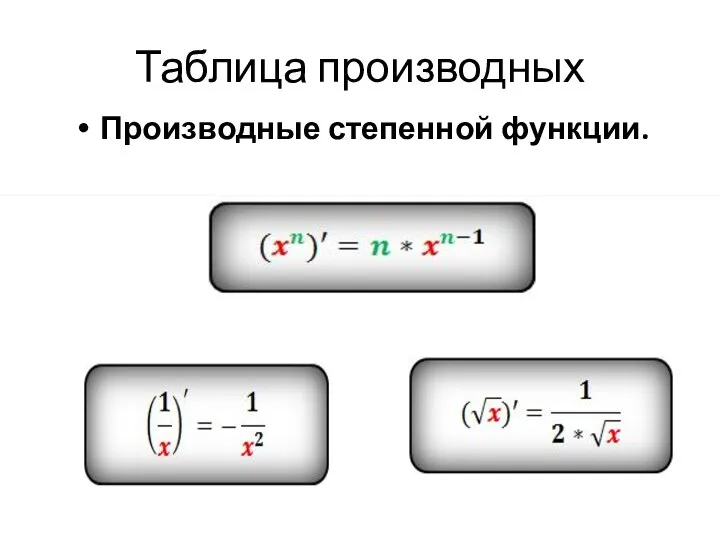
Слайд 3Таблица производных
Производные показательной функции.

Слайд 4Таблица производных
Производные логарифмической функции.
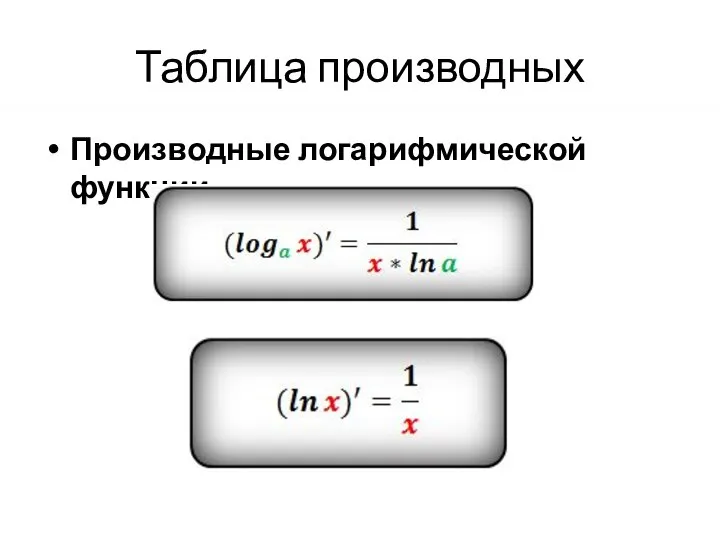
Слайд 5Таблица производных
Производные тригонометрической функции.

Слайд 6Таблица производных
Производные обратной тригонометрической функции.
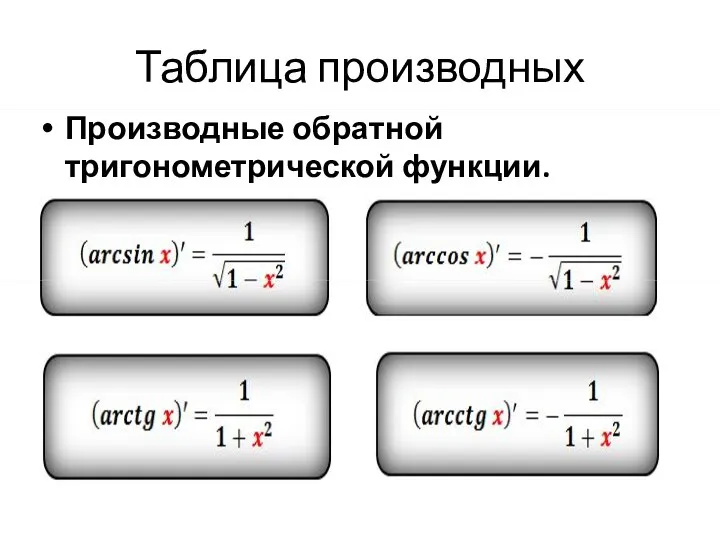
Слайд 7Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале

(a; b) функции, С – постоянная.
Слайд 8Алгоритм вычисления сложной функции
определить внутреннею функцию
определить внешнею функцию
найти производную

внешней функции
найти производную внутренней функции
найти произведение производной внешней на производную внутренней функции
Слайд 11 Если f!(х)≥0 , то функция у= f(х) возрастает .
Если f!(х)≤0
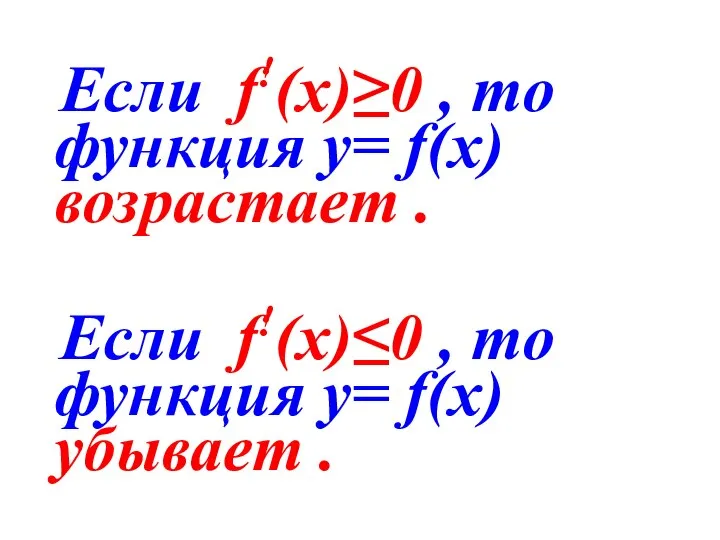
, то функция у= f(х) убывает .
Слайд 12Внутренние точки области определения функции, в которых производная функции равна нулю, называют

стационарными, а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует – критическими.
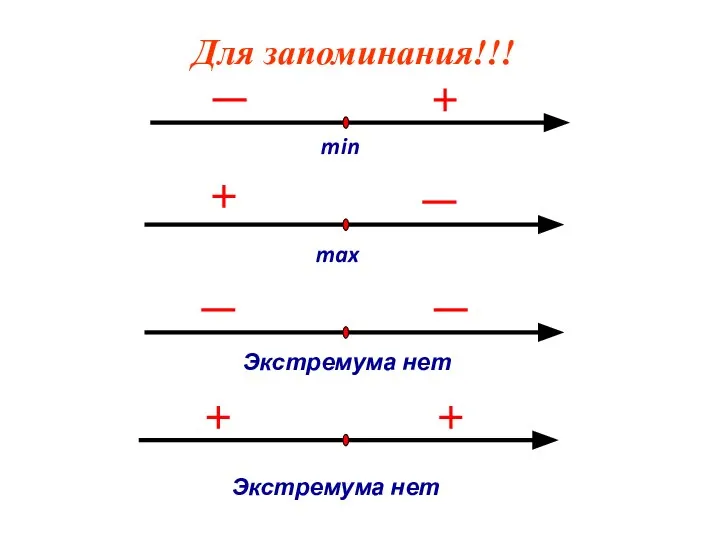
Слайд 13Для запоминания!!!
min
max
Экстремума нет
Экстремума нет
Слайд 15Если вторая производная функции у = f (х) на данном интервале положительна,

то кривая вогнута ,
а если отрицательна – выпукла.
Слайд 16Точки, в которых выпуклость
меняется на вогнутость или наоборот,
называются точками перегиба










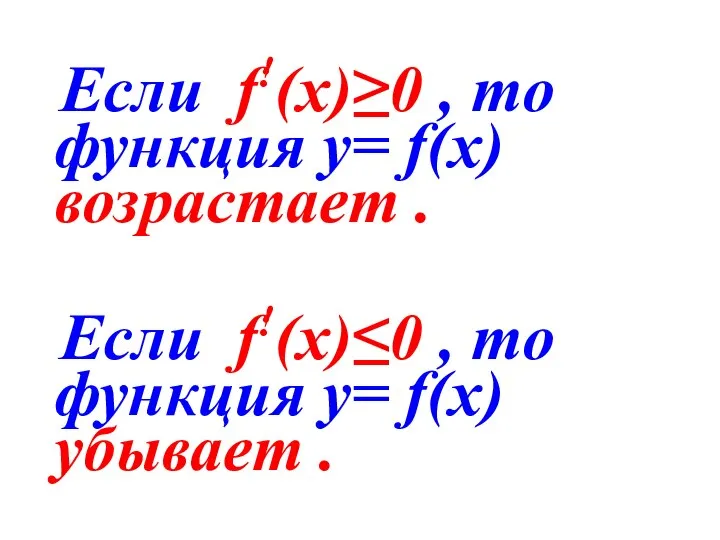





 Движение и виды движения
Движение и виды движения 5_vektory
5_vektory Степень с целым показателем. Блиц-опрос
Степень с целым показателем. Блиц-опрос Классические алгоритмы на графах
Классические алгоритмы на графах Несложная тригонометрия
Несложная тригонометрия Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Золотое сечение
Золотое сечение Системы с цилиндрическим фазовым пространством
Системы с цилиндрическим фазовым пространством Таблица сложения
Таблица сложения Сумма углов в треугольнике
Сумма углов в треугольнике Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Сечение тетраэдра
Сечение тетраэдра Математика. Занятие Число 7
Математика. Занятие Число 7 Решение задачи дуффинга регуляризованными методами неполного прогноза
Решение задачи дуффинга регуляризованными методами неполного прогноза Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений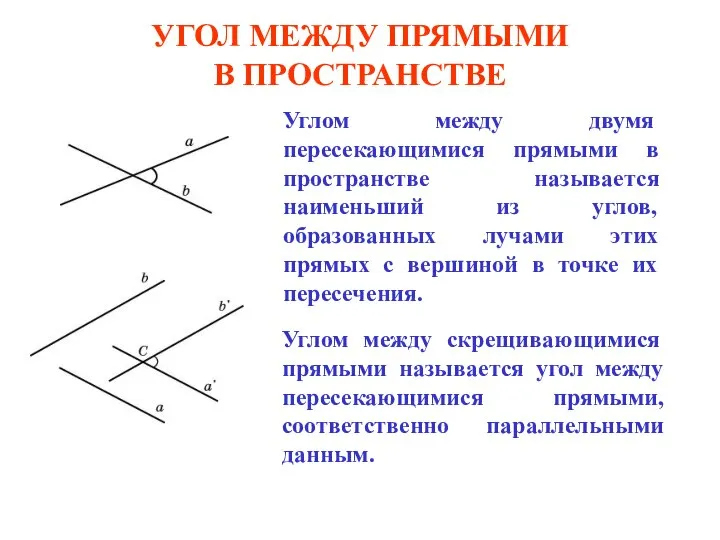 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Арифметический корень степени n
Арифметический корень степени n Обыкновенные дроби
Обыкновенные дроби Производная сложной функции
Производная сложной функции Симплекс метод. Лекция 5
Симплекс метод. Лекция 5 Свойства равнобедренных треугольников
Свойства равнобедренных треугольников Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Решение системы уравнений первой степени с двумя неизвестными
Решение системы уравнений первой степени с двумя неизвестными