Содержание
- 2. Тема 2. Парная регрессия и корреляция 2.1. Основные цели и задачи регрессионного анализа 2.2. Постановка задачи,
- 3. Виды связи между явлениями (переменными Y и X): Функциональная (жестко детерминированная). ПеременныеY и X являются неслучайными,
- 4. По направлению связи различают: а) прямую; б) обратную.
- 5. По виду аналитической функции различают: а) линейную связь; б) нелинейную связь.
- 6. Постановка задачи регрессии Будем предполагать, что объясняющая переменная X оказывает воздействие на значения переменной Y, которая,
- 7. Постановка задачи регрессии Пусть мы располагаем n парами выборочных наблюдений над двумя переменными X и Y:
- 8. Модель регрессии между Y и X имеет вид Yi =f(Xi)+εi, i=1,…,n, f(X) - функция регрессии Y
- 9. Выбор вида аналитической функции f(X) используется априорная информация о содержательной экономической сущности анализируемой зависимости – аналитический
- 10. Парная линейная регрессия и корреляция Пусть функция f – линейная. Тогда модель парной линейной регрессии примет
- 11. Показатели направления и степени тесноты связи Для того чтобы иметь основание включить объясняющую переменную X в
- 12. Коэффициент ковариации
- 13. Для выявления влияния стажа работы (X) в годах на выработку (Y) в штуках в смену из
- 14. Задание Оценить параметры модели парной линейной регрессии; Записать уравнение регрессии; Проверить значимость уравнения регрессии в целом;
- 15. Рассчитать: Среднюю арифметическую Моду Медиану Дисперсию: а) неисправленную; б) исправленную Среднее квадратическое отклонение Коэффициент вариации Коэффициент
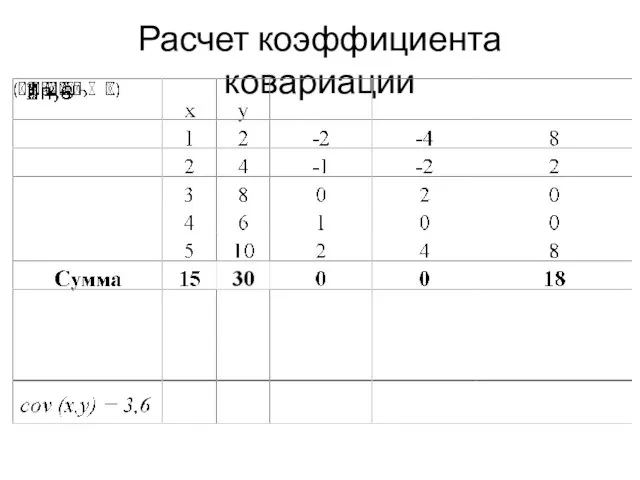
- 16. Расчет коэффициента ковариации
- 17. Линейный коэффициент корреляции К.Пирсона
- 18. Дисперсия
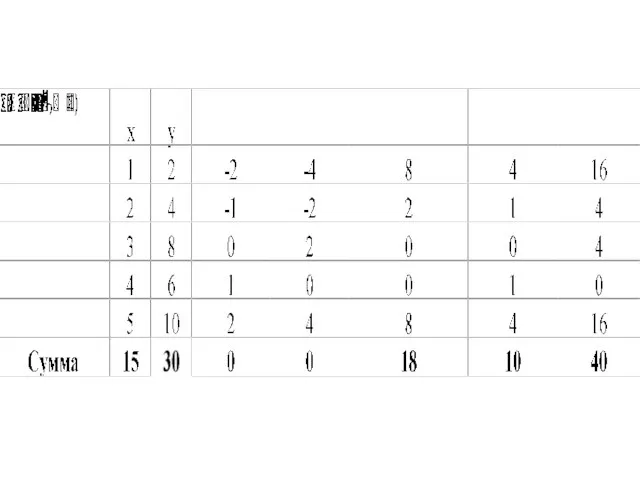
- 20. Дисперсия
- 21. Cреднее квадратическое отклонение
- 22. Cреднее квадратическое отклонение
- 23. Линейный коэффициент корреляции К.Пирсона
- 24. Коэффициент детерминации
- 25. Коэффициент детерминации показывает, какая часть колеблемости (вариации) Y объясняется колеблемостью (вариацией) X. Коэффициент детерминации показывает, на
- 26. Проверка значимости коэффициента корреляции Формулируем гипотезы (линейной корреляцонной связи между X и Y нет; коэффициент корреляции
- 27. Устанавливаем уровень значимости α
- 28. Находим наблюдаемое значение критерия
- 29. Находим наблюдаемое значение критерия
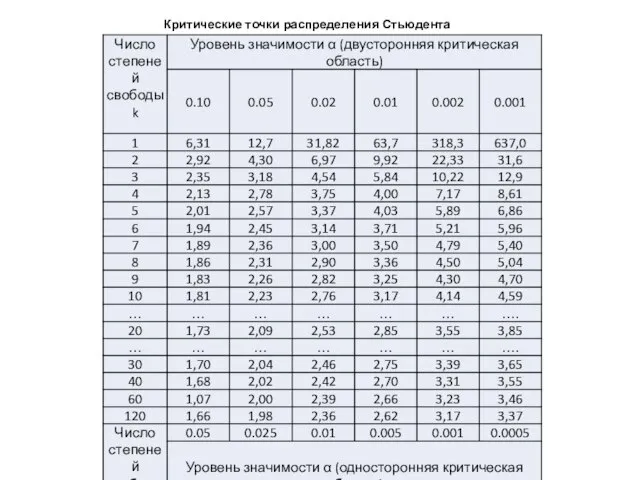
- 30. Находим критическое значение критерия по таблице Стьюдента по уровню значимости α и по числу степеней свободы
- 31. Критические точки распределения Стьюдента
- 32. Если |tнабл.| > tкр., то нулевая гипотеза отклоняется в пользу альтернативной о статистической значимости коэффициента корреляции.
- 33. С надежностью, большей 0,95, и риском ошибиться, меньшим 0,05, можно утверждать, что между X и Y
- 34. Доверительный интервал коэффициента корреляции в генеральной совокупности
- 35. С надежностью 0,95 и риском ошибиться 0,05 можно утверждать, что коэффициент корреляции между X и Y
- 36. Модель парной линейной регрессии Y = β0+β1X+ε, где: β0 - свободный член (константа); β1 – коэффициент
- 37. Задачи регрессионного анализа Для любых значений объясняющей переменной X построить наилучшие по некоторому критерию оценки для
- 38. Эмпирическое уравнение регрессии:
- 40. Модель и уравнение регрессии
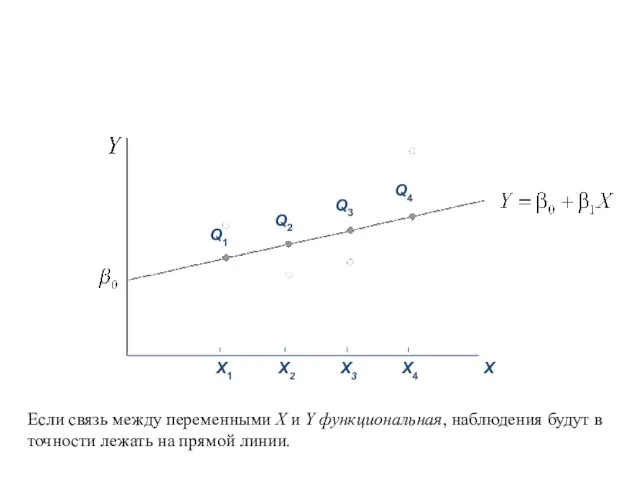
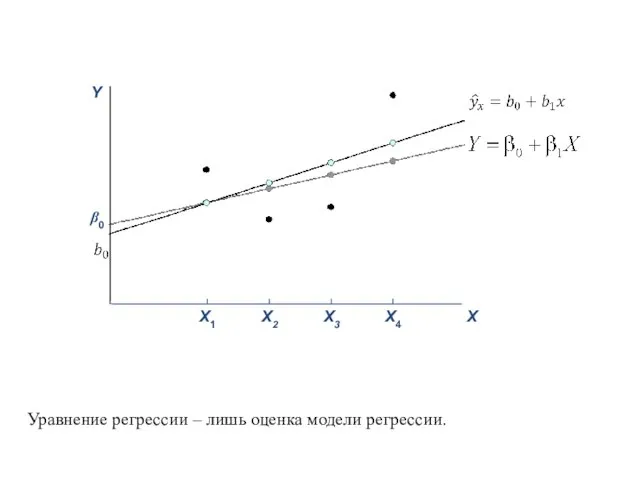
- 41. Если связь между переменными X и Y функциональная, наблюдения будут в точности лежать на прямой линии.
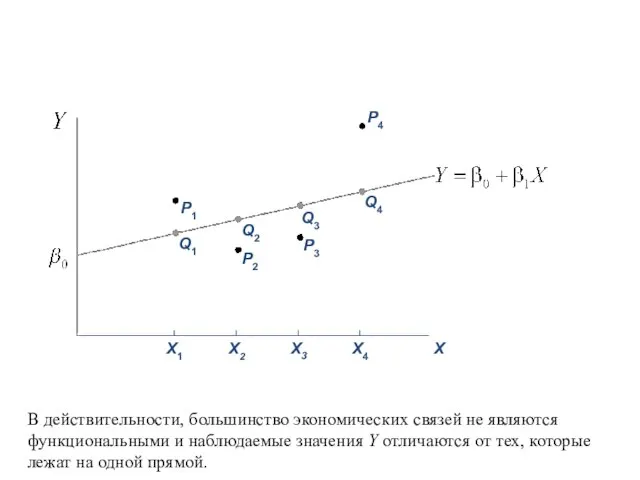
- 42. В действительности, большинство экономических связей не являются функциональными и наблюдаемые значения Y отличаются от тех, которые
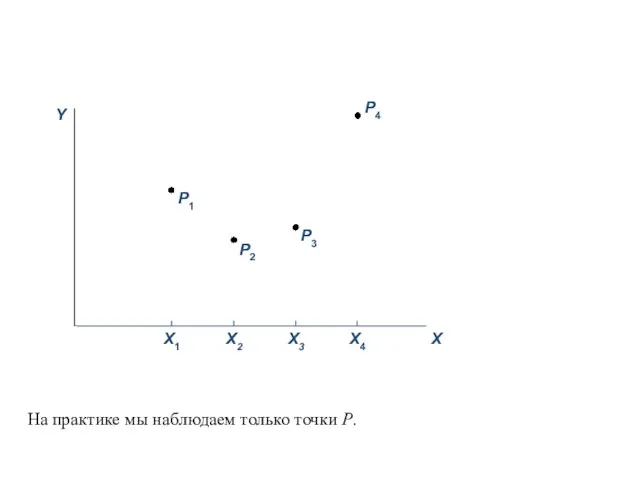
- 43. На практике мы наблюдаем только точки P.
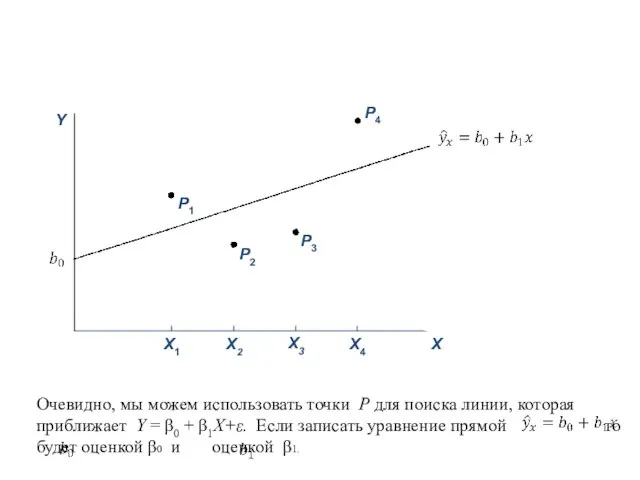
- 44. Очевидно, мы можем использовать точки P для поиска линии, которая приближает Y = β0 + β1X+ε.
- 45. Уравнение регрессии – лишь оценка модели регрессии.
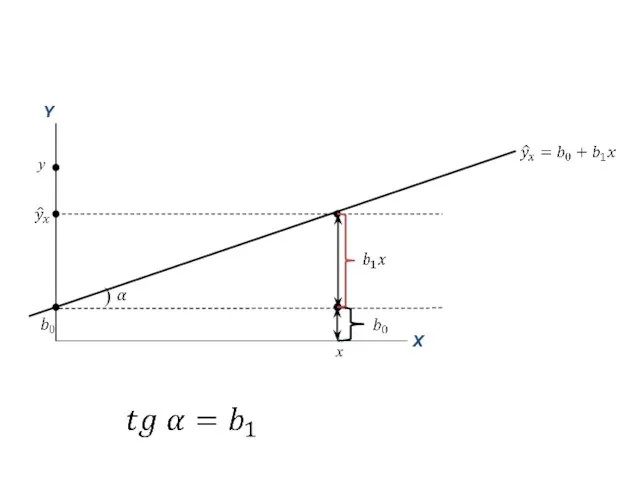
- 46. y x )
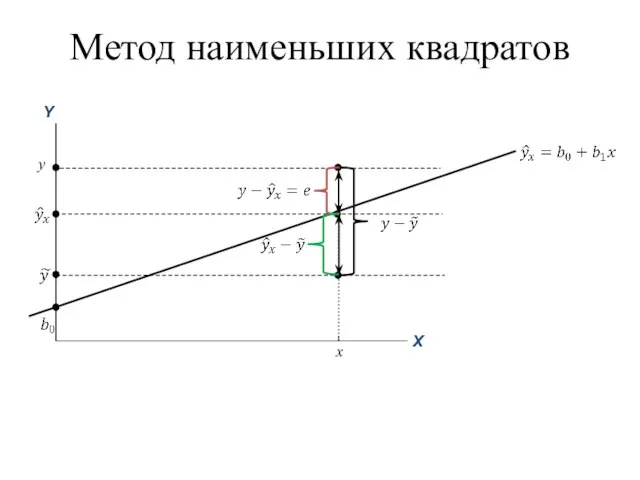
- 47. y x Метод наименьших квадратов
- 50. Принцип метода наименьших квадратов (МНК) заключается в выборе таких оценок b0 и b1, для которых сумма
- 51. Для определения оценок параметров модели регрессии b0 и b1 необходимо минимизировать выражение:
- 53. Отсюда получим формулы расчета оценок параметров модели регрессии
- 54. Для выявления влияния стажа работы (X) в годах на выработку (Y) в штуках в смену из
- 55. Расчет оценок параметров модели регрессии
- 56. Уравнение регрессии
- 57. Интерпретация коэффициента регрессии Коэффициент регрессии b1 показывает на сколько единиц увеличится (уменьшится) в среднем значение зависимой
- 58. Интерпретация константы Константа b0 показывает базисный (начальный) уровень, т.е. значение зависимой переменной Y при условии, что
- 59. Интерпретация коэффициента регрессии Коэффициент регрессии b1 показывает, что при увеличении стажа на 1 год выработка в
- 60. Интерпретация константы Константа b0 показывает, что средняя выработка рабочего, не имеющего стажа, составит 0,6 штуки в
- 61. Проверка статистической значимости уравнения регрессии в целом. Y не зависит от всех X, включенных в модель
- 62. Устанавливаем уровень значимости α
- 63. Найдем наблюдаемое значение критерия где n – число наблюдений, m – число параметров в модели регрессии
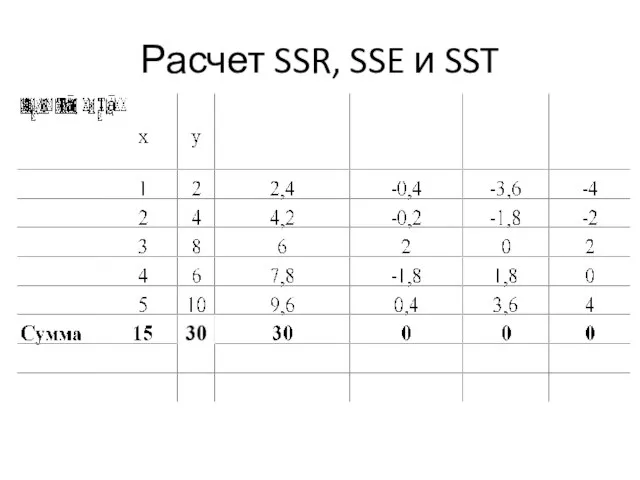
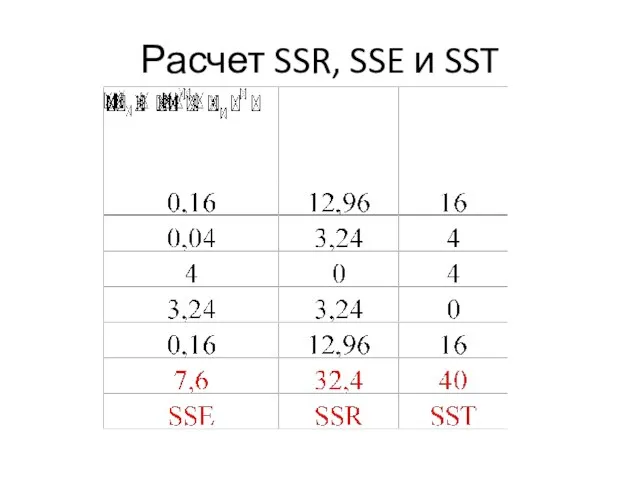
- 64. Расчет SSR, SSE и SST
- 65. Расчет SSR, SSE и SST
- 66. Найдем наблюдаемое значение критерия
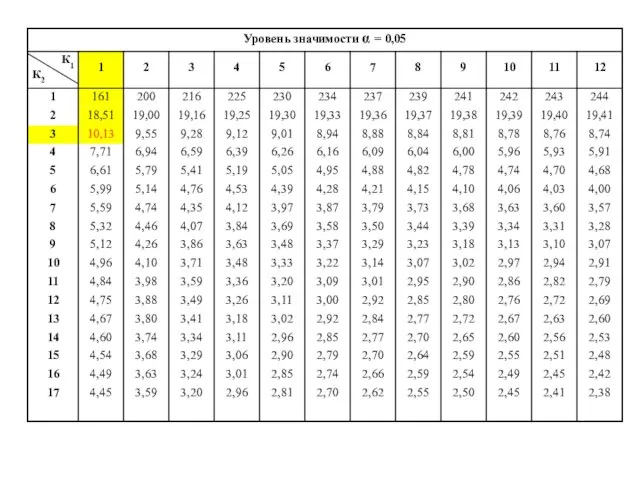
- 67. По таблице распределения Фишера найдем критическое значение критерия:
- 69. Если Fнабл.>Fкр., то нулевая гипотеза отклоняется в пользу альтернативной о статистической значимости уравнения регрессии в целом.
- 70. 12,79>10,13 С надежностью, большей 0,95, и риском ошибиться, меньшим 0,05, можно утверждать, что Y (выработка) зависит
- 71. Проверка статистической значимости коэффициента регрессии Сформулируем гипотезы Y не зависит от данного конкретного X (коэффициент регрессии
- 72. Устанавливаем уровень значимости α
- 73. Находим наблюдаемое значение критерия
- 74. Стандартная ошибка уравнения регрессии
- 75. Стандартная ошибка коэффициента регрессии
- 76. Находим наблюдаемое значение критерия
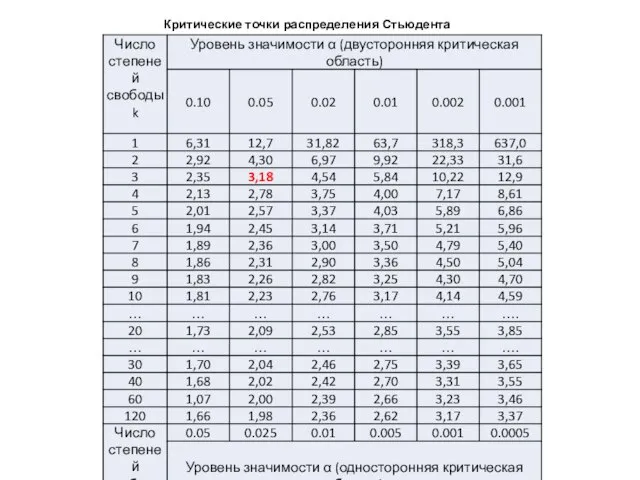
- 77. Находим критическое значение критерия по таблице Стьюдента по уровню значимости α и по числу степеней свободы
- 78. Критические точки распределения Стьюдента
- 79. Если |tнабл.|>tкр.,то нулевая гипотеза отклоняется в пользу альтернативной о статистической значимости коэффициента регрессии. Если |tнабл.|≤ tкр.,
- 80. 3,58>3,18 С надежностью, большей 0,95, и риском ошибиться, меньшим 0,05, можно утверждать, что Y (выработка) зависит
- 81. Проверка статистической значимости константы Сформулируем гипотезы Константа не значима (незначимо отличается от 0) Константа значима (значимо
- 82. Устанавливаем уровень значимости α
- 83. Наблюдаемое значение критерия
- 84. Стандартная ошибка константы:
- 85. Наблюдаемое значение критерия
- 86. Находим критическое значение критерия по таблице Стьюдента по уровню значимости α и по числу степеней свободы
- 87. Если |tнабл.|>tкр.,то нулевая гипотеза отклоняется в пользу альтернативной о статистической значимости константы. Если |tнабл.|≤ tкр., оснований
- 88. 0,36 На уровне значимости α=0,05 константа не значима.
- 89. Доверительные интервалы неизвестных значений β1 и β0
- 90. Доверительный интервал неизвестного значения β1
- 91. С надежностью 0,95 и риском ошибиться 0,05 можно утверждать, что коэффициент регрессии в генеральной совокупности (для
- 92. Доверительный интервал неизвестного значения β0
- 93. С надежностью 0,95 и риском ошибиться 0,05 можно утверждать, что константа в генеральной совокупности (для всех
- 94. Точечный прогноз по уравнению регрессии
- 95. Точечный прогноз по уравнению регрессии
- 96. X Y
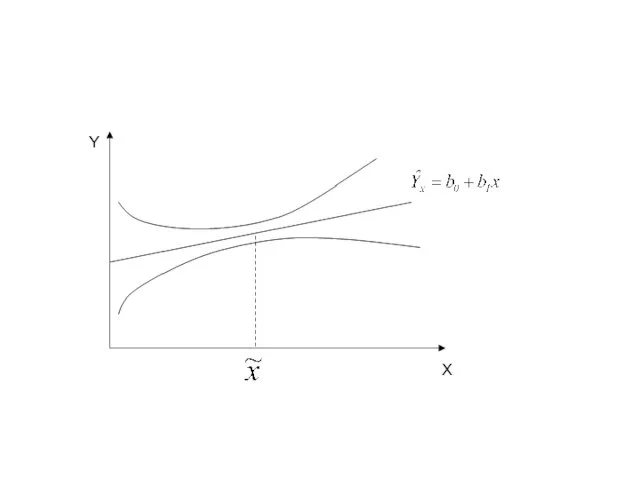
- 97. Интервальный прогноз неизвестного среднего генерального значения Y
- 100. Интервальный прогноз неизвестного среднего генерального значения Y
- 101. С надежностью 0,95 можно утверждать, что средняя выработка рабочих со стажем 2.5 года находится в интервале
- 102. Интервальный прогноз неизвестного индивидуального значения Y
- 103. Интервальный прогноз неизвестного индивидуального значения Y
- 105. Скачать презентацию










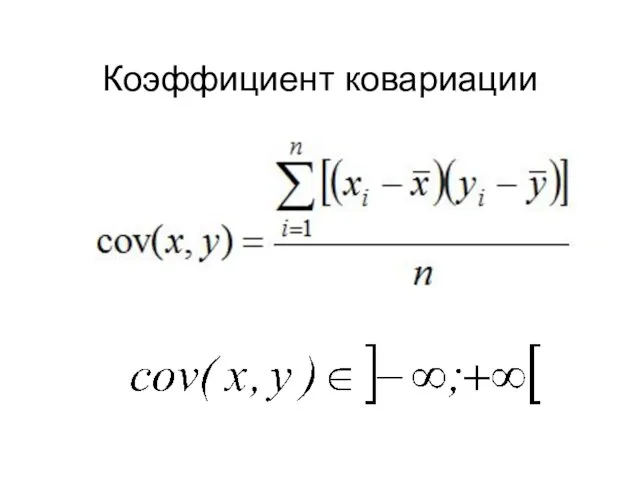




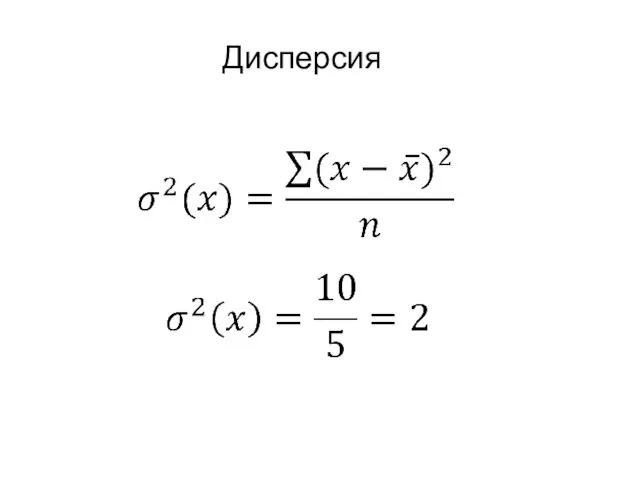
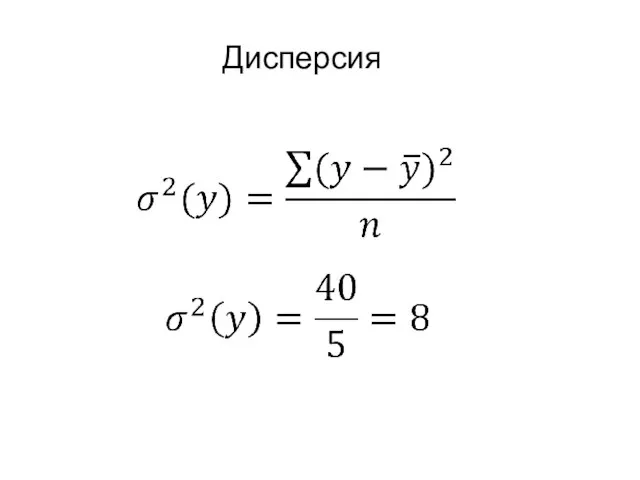

















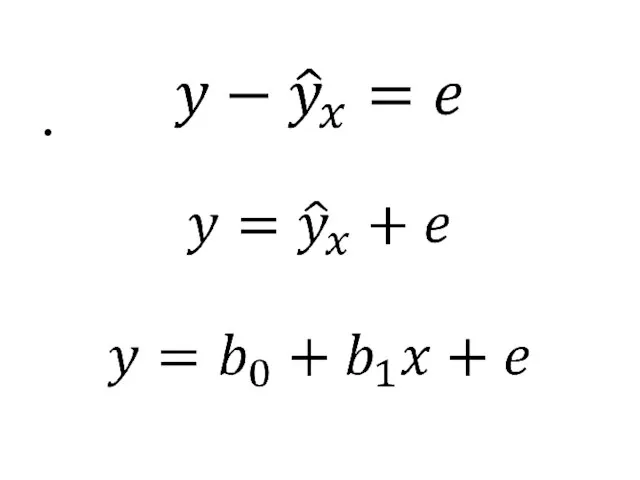
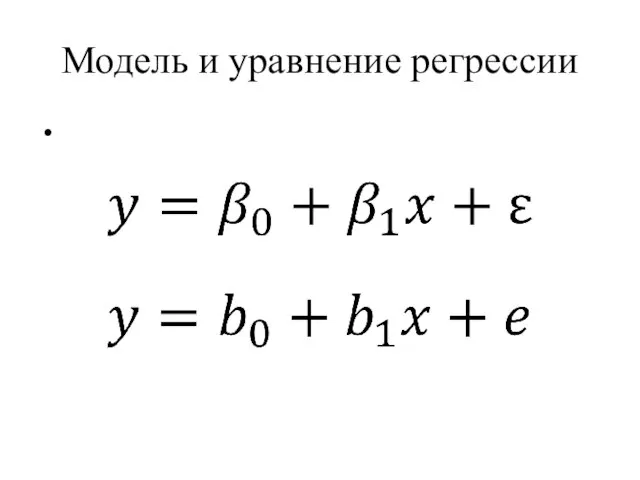
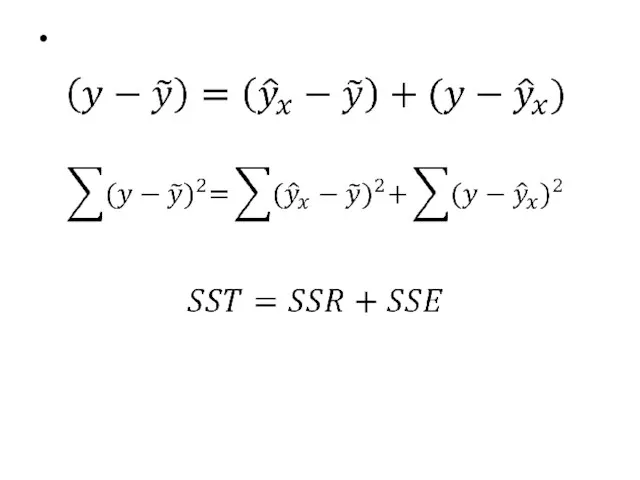









































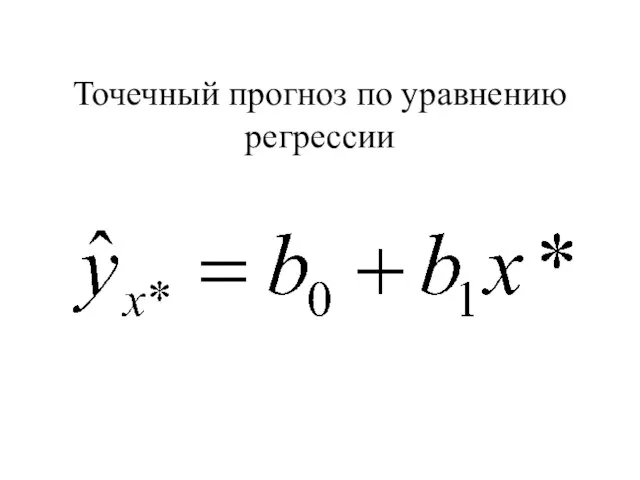


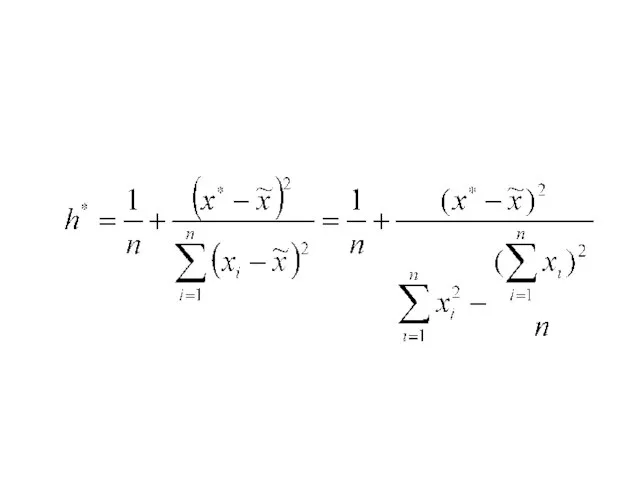
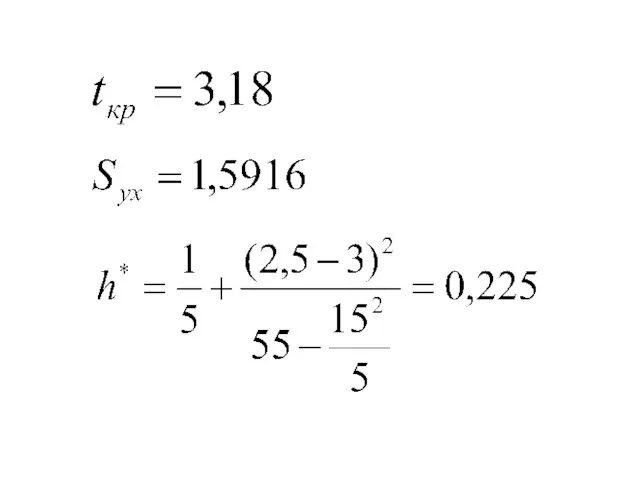




 Понятие интеграла
Понятие интеграла Решение комбинаторных задач
Решение комбинаторных задач Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций
Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций Проценты. 6 класс
Проценты. 6 класс Формула полной вероятности
Формула полной вероятности Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Приемы устных вычислений трехзначных чисел
Приемы устных вычислений трехзначных чисел Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Презентация на тему РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері
L(q(x), h, H) шекаралық есептің меншікті мәндері және A(A) характеристикалық функцияның нөлдері Преобразование дробей с помощью основного свойства
Преобразование дробей с помощью основного свойства Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы
Линейная алгебра. Матрицы. Основные понятия. Действия над матрицами. Поиск обратной матрицы Проценты (5)
Проценты (5) Длиннее, короче. Одинаковые по длине
Длиннее, короче. Одинаковые по длине Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Занимательная геометрия
Занимательная геометрия Решение неравенств второй степени с одной переменной. Определение
Решение неравенств второй степени с одной переменной. Определение Параллельность прямой и плоскости
Параллельность прямой и плоскости Методы решения тригонометрических уравнений. 10 класс
Методы решения тригонометрических уравнений. 10 класс Найдите лишнюю фигуру и объясните свой выбор
Найдите лишнюю фигуру и объясните свой выбор Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Нахождение угла между двумя прямыми в пространстве
Нахождение угла между двумя прямыми в пространстве Предмет и методы теории систем. Лекция 1
Предмет и методы теории систем. Лекция 1 ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах
ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах Площадь поверхности цилиндра
Площадь поверхности цилиндра Интерактивная игра-тренажер по математике
Интерактивная игра-тренажер по математике Кривые линии. Комплексный чертеж поверхности
Кривые линии. Комплексный чертеж поверхности