Слайд 2Симметрия
Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны

с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей.
Слайд 3Центральная симметрия
Пусть в пространстве задана точка О . Отображение пространства, при котором

точка О переходит в себя, а произвольная точка М, отличная от О, — в такую точку М’, что точка О является серединой отрезка ММ’, называется симметрией относительно точки О или центральной симметрией. Точка О называется центром симметрии, а о точках М и М’ говорят, что они симметричны относительно точки О.
Слайд 4Центральная симметрия
Теорема 1. Центральная симметрия — перемещение.
Теорема 2. Перемещение пространства является центральной

симметрией тогда и только тогда, когда оно изменяет направления на противоположные.
Теорема 3. Центральная симметрия переводит прямую в себя или в параллельную ей прямую, плоскость — в себя или в параллельную ей плоскость.
Слайд 5Осевая симметрия
Определение: Точка М1 , не лежащая на прямой L , называется

симметричной точке M относительно прямой L, если прямая является серединным перпендикуляром к отрезку MM1.
Если точка M лежит на прямой L, то говорят, что точка M симметрична самой себе относительно прямой L.
Прямая L называется осью симметрии.
Слайд 6Свойства осевой симметрии
Свойства осевой симметрии.
Преобразование, обратное осевой симметрии, есть та же осевая

симметрия.
Осевая симметрия переводит прямую, параллельную оси в параллельную ей прямую.
Неподвижными точками являются точки, лежащие на оси симметрии. Неподвижными прямыми являются ось симметрии и прямые, ей перпендикулярные.
Композицией двух осевых симметрий с параллельными осями является параллельный перенос на вектор, перпендикулярный данным прямым и по модулю в два раза больший, чем расстояние между ними (направление зависит от порядка композиции).
Композицией двух осевых симметрий с пересекающимися осями является поворот с центром в точке их пересечения на угол, в два раза больший угла между данными прямыми (направление зависит от порядка композиции).
Слайд 7Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная

для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.






 Предел функции (часть 3)
Предел функции (часть 3) Подобные треугольники. Признаки подобия треугольников
Подобные треугольники. Признаки подобия треугольников Элементы комбинаторики
Элементы комбинаторики Уравнение сферы
Уравнение сферы Геометрические приложения двойных интегралов
Геометрические приложения двойных интегралов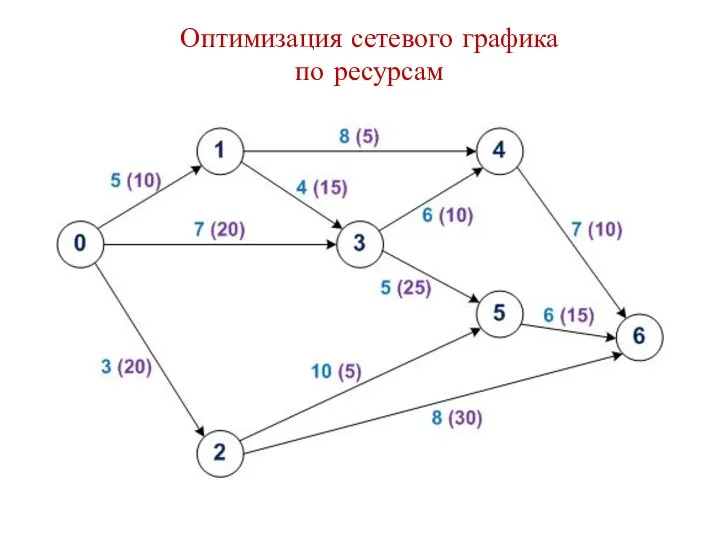 Оптимизация сетевого графика по ресурсам
Оптимизация сетевого графика по ресурсам Сложение дробей
Сложение дробей Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Плоскости
Плоскости Показательные уравнения
Показательные уравнения Проценты чисел
Проценты чисел Случаи сложения вида +8, +9
Случаи сложения вида +8, +9 Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Волшебная страна - Геометрия
Волшебная страна - Геометрия Решение занимательных задач
Решение занимательных задач Рейтинг-контроль
Рейтинг-контроль Функции и графики
Функции и графики Несложная тригонометрия
Несложная тригонометрия Производная
Производная Надежность технических систем
Надежность технических систем Algebraic constructions generated by causal structure of space-times
Algebraic constructions generated by causal structure of space-times Булева алгебра. Семинар №2
Булева алгебра. Семинар №2 Congruenţa triunghiurilor dreptunghice
Congruenţa triunghiurilor dreptunghice Построение графиков функций при помощи геометрических преобразований
Построение графиков функций при помощи геометрических преобразований Преобразование функцмй
Преобразование функцмй Математический диктант
Математический диктант