Слайд 2СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки, лежащие на одном

перпендикуляре к данной плоскости (прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (прямой).
Слайд 3Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости

симметрии), если ее точки попарно обладают указанным свойством.
Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.
Слайд 4Виды симметрии:
осевая
центральная (поворот на 180)
скользящая
пространственная (относительно плоскости)
Вращательная

Слайд 5ОСЕВАЯ СИММЕТРИЯ
Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Слайд 7ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
- это такое свойство геометрической фигуры, когда любой точке, расположенной по

одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.
Поворот на 180 градусов
Слайд 9СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ
Симметрия относительно плоскости - это такое свойство геометрической фигуры,

когда любой точке, расположенной по одну сторону плоскости, всегда будет соотвествовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.
Слайд 10ЗЕРКАЛЬНАЯ СИММЕТРИЯ-ЭТО ТАКЖЕ СИММЕТРИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТИ










 Обучающие слайды
Обучающие слайды Многочлены над числовыми полями
Многочлены над числовыми полями Приёмы умножения числа 2
Приёмы умножения числа 2 Теория вероятностей
Теория вероятностей Математика. Занятие Число 7
Математика. Занятие Число 7 Где логика. Игра
Где логика. Игра Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Математика в биологии
Математика в биологии Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Презентация на тему КВН по математике
Презентация на тему КВН по математике  Задачи, обратные данной
Задачи, обратные данной Арифметическая игра. Чебурашка и числовые домики
Арифметическая игра. Чебурашка и числовые домики Арифметическая прогрессия
Арифметическая прогрессия Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения)
Спецификация КИМ ЕГЭ 2015 г. Проверяемые требования (умения) Модель Мальтуса
Модель Мальтуса Презентация на тему СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ
Презентация на тему СЛОЖЕНИЕ ЧИСЕЛ С ПОМОЩЬЮ КООРДИНАТНОЙ ПРЯМОЙ  Умножение двузначных чисел
Умножение двузначных чисел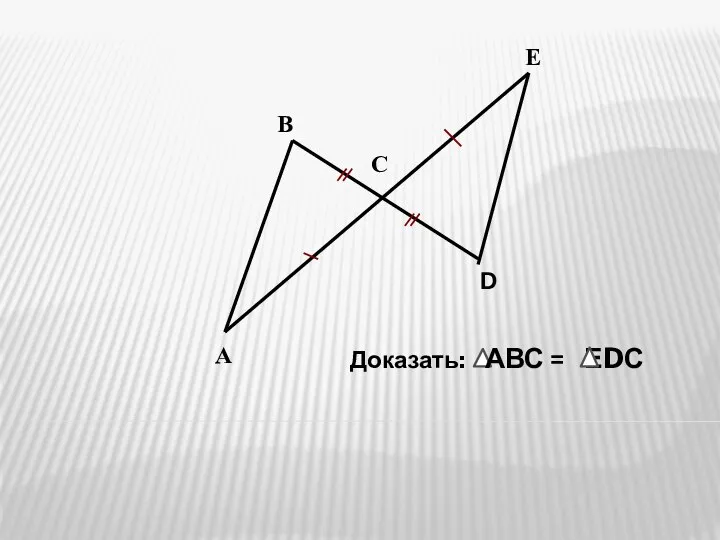 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Фотоальбом. Ребус
Фотоальбом. Ребус Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность
Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность Согласование существительных с числительными
Согласование существительных с числительными Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Алгоритм построения графиков, содержащих модуль
Алгоритм построения графиков, содержащих модуль Плоскость в пространстве
Плоскость в пространстве Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Логарифмические уравнения и их системы
Логарифмические уравнения и их системы Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность