Высоты треугольников

Определение
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону этого треугольника.

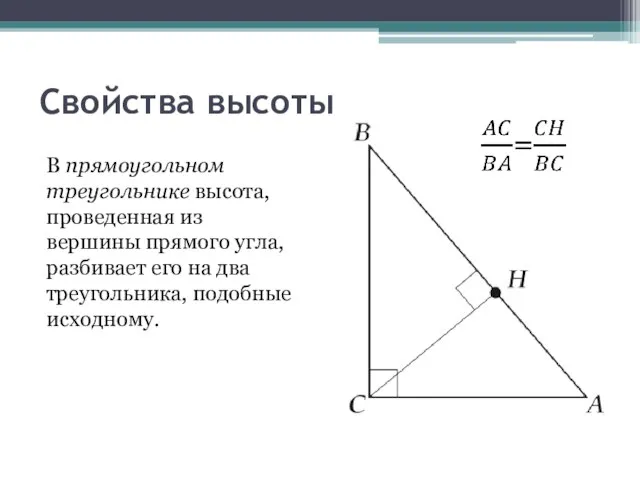
Свойства высоты
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобныеисходному.

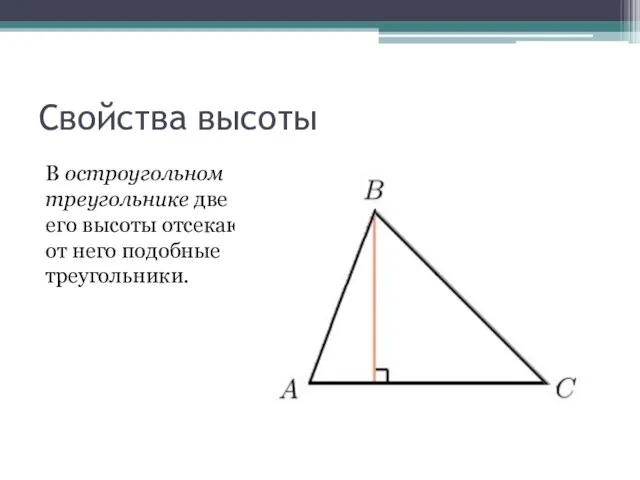
Свойства высоты
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

Свойства высоты
В равнобедренном треугольнике, третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.

Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике ABC длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной C на отрезки m и n, соответствующие катетам b и a, то верны следующие равенства:

Медианы и высоты в равностороннем треугольнике
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. А в равносторонних треугольниках медианы и высоты - одно и то же.

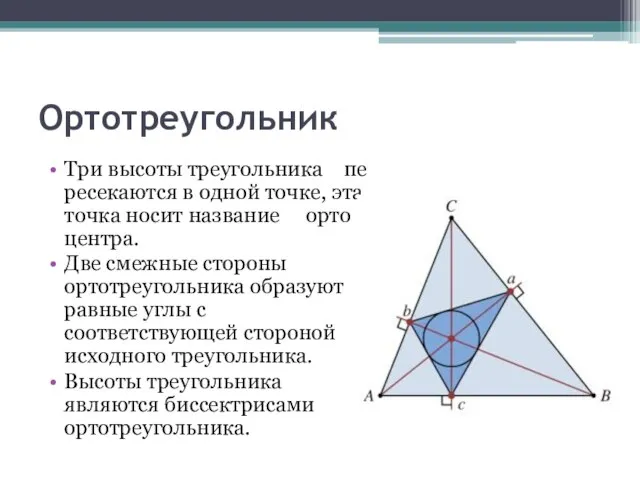
Ортотреугольник
Три вы­со­ты тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке, эта точка носит на­зва­ние ор­то­цен­тра.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
Высоты треугольника являются биссектрисами ортотреугольника.

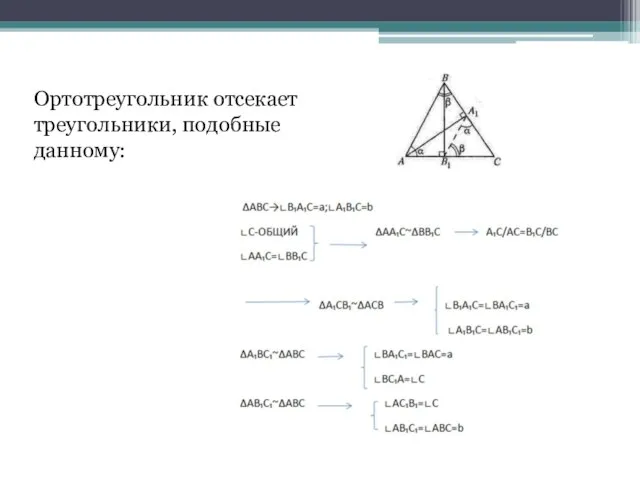
Ортотреугольник отсекает треугольники, подобные данному:

Теорема о свойстве биссектрис ортотреугольника

Окружность девяти точек
Основания высот, середины сторон и середины отрезков, соединяющих ортоцентр —точку пересечения высот —с вершинами треугольника, лежат на одной окружности — окружности девяти точек.

Прямая Эйлера
Центр описанной окружности, центр тяжести, центр окружности девяти точек и ортоцентр лежат на одной прямой — прямой Эйлера.

Теорема Гамильтона
Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.

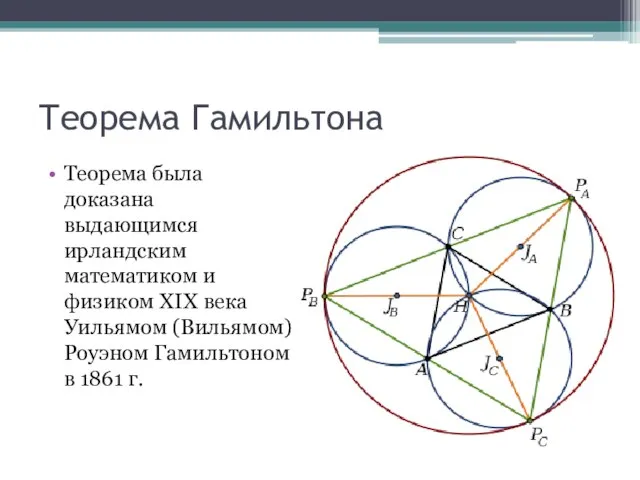
Теорема Гамильтона
Теорема была доказана выдающимся ирландским математиком и физиком XIX века Уильямом (Вильямом) Роуэном Гамильтоном в 1861 г.