предел. непрерывность

Бесконечно малые функции
Пусть функция определена в окрестности точки a, кроме, быть может, самой точки a.
Функция называется бесконечно малой функцией (б.м.ф.) при x, стремящемся к a, если

Функция называется бесконечно малой функцией (б.м.ф.) при или , если
или
Определение б.м.ф. на бесконечности

Примеры.
б.м.ф. при
б.м.ф. при
б.м.ф. при
б.м.ф. при

Свойства бесконечно малых функций

Теорема 5 (сумма б.м.ф.)
Если - б.м.ф. при ,
есть также
б.м.ф. при
то их сумма

Доказательство:
б.м.ф. при
Функция
б.м.ф. при
Функция
б.м.ф. при

Теорема 6 (произведение б.м.ф. на ограниченную функцию)
Если функция является
б.м.ф. при
а функция f(x) ограничена в окрестности точки a,
есть б.м.ф. при
то произведение

Доказательство:
- ограничена в окрестности точки a.
- б.м.ф. при
- б.м.ф. при

Пример.
- б.м.ф. при
-ограничена в любой проколотой окрестности точки x=0. - б.м.ф. при

Следствие.
Если
- б.м.ф. при
а функция f(x) имеет конечный предел в точке a, то произведение
- б.м.ф. при

Лемма.
Если функция f(x) в точке x=a имеет предел, отличный от нуля , то функция
- ограничена в окрестности точки x=a.

Доказательство:
- ограничена в проколотой окрестности точки x=a.
определена и

Теорема 7
Если
- б.м.ф. при
а функция f(x) в точке x=a имеет предел, отличный от нуля , то частное
- есть б.м.ф. при

Доказательство:
- ограничена в проколотой окрестности точки x=a.
имеет конечный предел в точке x=a.
- б.м.ф. при

Теорема 8(связь функции, имеющей предел, с её пределом и бесконечно малой функцией)
Пусть функция f(x) определена в окрестности точки x=a, кроме, быть может, самой точки a.
Для того, чтобы число А было пределом функции f(x)
при , необходимо и достаточно, чтобы f(x) можно было представить в виде суммы
Где
- б.м.ф. при

Необходимость.
Положим
и докажем, что
- б.м.ф. при
- б.м.ф. при
Достаточность. - б.м.ф. при
для тех же значений x .

Теорема 9 (арифметические операции над пределами)
Пусть функция и определены в окрестности точки x=a, кроме, быть может, самой точки a.
Если и имеют пределы в точке x=a, то имеют пределы также их сумма , разность , произведение и частное при
условии , причём

Доказательство.
где
- б.м.ф. при
- б.м.ф. при
- б.м.ф. при

Следствие.
Постоянный множитель можно выносить за знак предела.

Определение бесконечно большой функции
Пусть функция определена в окрестности точки a, кроме, быть может, самой точки a.
Если для любого, как угодно большого, числа M>0 существует такое число , что для всех , удовлетворяющих условию
выполняется неравенство
То функцию f(x) называют бесконечно большой функцией при

f(x) – б.б.ф.
f(x) – положительная б.б.ф.
f(x) – отрицательная б.б.ф.

Пример.
Функция
Решение.

Теорема о связи бесконечно больших и бесконечно малых функций
.
Если и в некоторой окрестности точки a, кроме, быть может самой точки a, , то функция
И, наоборот, если
то

Следовательно,
Обозначим
Доказательство.
Пусть
Обратное утверждение доказывается аналогично.

Односторонние пределы
Пусть функция f(x) определена только слева (или только справа) от а, т.е. в интервале х < а (х > а).
Определение 1.
Число а называется левосторонним пределом функции f(x) при
(х < а), если
Определение 2.
Число а называется правосторонним пределом функции f(x) при
(х >а), если

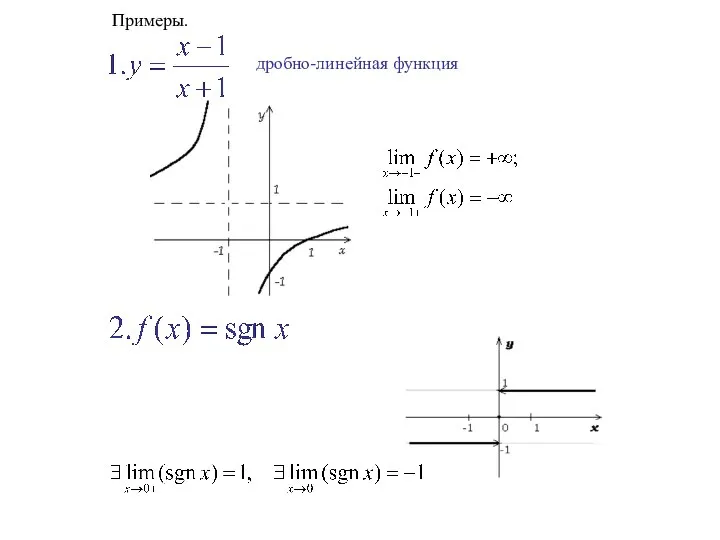
дробно-линейная функция
Примеры.

Теорема
Для того, чтобы функция f(x) имела предел в точке a, необходимо и достаточно, чтобы существовали пределы функции f(x) в точке a справа и слева и они были равны между собой.

Доказательство.
Обратно,