Приближенные вычисления

вспомним
Что называется модулем числа?

Определите, чему равен модуль разности:
5 и 3, 7
-9, 5 и 9;

Правило округления.
При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна 5, то последнюю оставшуюся цифру увеличивают на 1. Если же первая оставшаяся за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют.

При округлении десятичных дробей до десятых, до сотых, до тысячных и т.д. получаются приближенные значения с точностью до 0,1; 0,01; 0,001 и т.д.

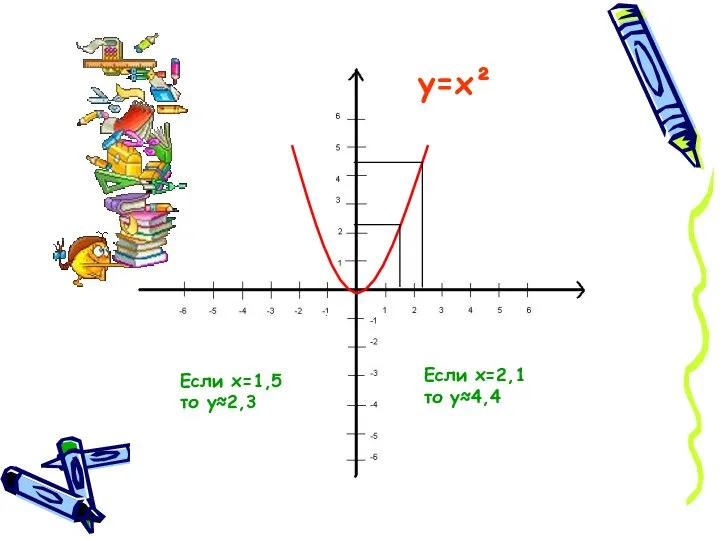
Если х=1,5 то у≈2,3
Если х=2,1 то у≈4,4
у=х²

По формуле у= х² найдем точные значения этой функции:
Если х=1,5
Если х=2,1
то у=1,5² =2,25
то у=2,1² =4,41

На сколько отличается приближенное значение от точного?
2,3-2,25=0,05
4,41-4,4=0,01

Вывод: Чтобы узнать, на сколько приближенное значение отличается от точного, надо из большего числа, вычесть меньшее.
Надо найти модуль разности точного и приближенного значения. Этот модуль разности называют абсолютной погрешностью.

Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.

А относительная погрешность оценивает качество измерения и
выражается в процентах.

Если х ≈ α, где х – точное значение, а α – приближенное,
то абсолютная погрешность будет равна │х – α │,
а относительная:
│х – α │∕ │α│, умноженное на 100%

1 2
1
2
3
4
Выполните упражнение:
При х=1,2
у≈1,6
При х=1,5
у≈3,4
По графику - приближенное значение
По формуле – точное значение
При х=1,2
у=1,2³=1,728
При х=1,5
у=1,5³=3,375
Чему равна абсолютная погрешность?
\1,728-1,6\=\0,128\=0,128
\3,375-3,4\=\0,025\=0,025
у=х³

Вычислим относительную погрешность этих приближений:
0,128 : │1,6│= 0, 128 : 1,6 = 0,08 = 8%
0,025 : │3,4│= 0, 025:3,4 = 0,007 = 0,7%

Она зависит от многих причин. Если приближенное значение получено при измерении, то его точность зависит от прибора, с помощью которого выполнялось измерение. Никакое измерение не может быть выполнено совершенно точно. Даже сами меры заключают в себе погрешность. Изготовить совершенно точные метровые линейки, килограммовую гирю, литровую кружку чрезвычайно трудно и закон допускает при изготовлении некоторую погрешность.

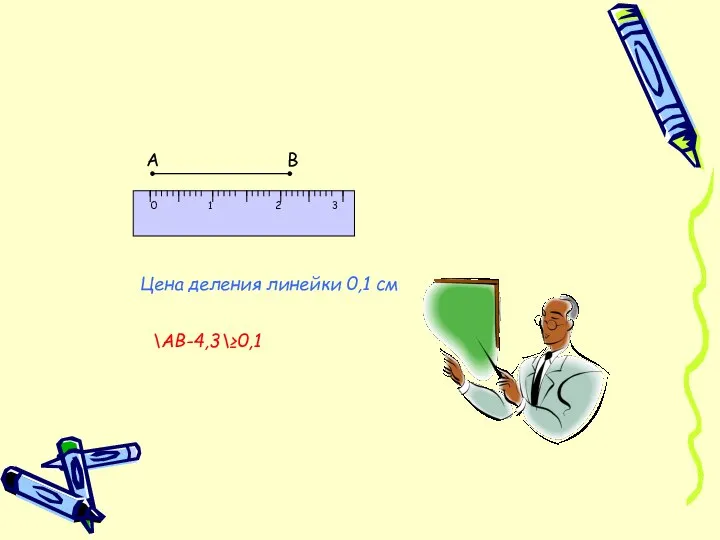
0 1 2 3
А
В
Цена деления линейки 0,1 см
\АВ-4,3\≥0,1

Например, при изготовлении метровой линейки допускается погрешность 1мм. Само измерение тоже вводит неточность, погрешность в гирях, весах. Например на линейке, которой мы пользуемся, нанесены деления через 1мм, т.е. 0,1см, значит точность измерения этой линейкой до 0,1 ( ≤ 0,1). На медицинском термометре деления через 0,10 , значит точность до 0,1 ( ≤ 0,1). На весах деления нанесены через 200г, значит точность до 200 ( ≤ 200).
Округляя десятичную дробь до десятых точность будет до 0,1 ( ≤ 0,1); до сотых – точность до 0,01 ( ≤ 0,01).
Точнейшие в мире измерения производятся в лабораториях Института мер.

Всегда ли можно найти абсолютную и относительную погрешности?

Не всегда можно найти абсолютную погрешность, так как неизвестно
точное значение величины, а отсюда и относительную погрешность.
В этом случае принято считать что абсолютная погрешность не превосходит цены деления шкалы прибора. Т.е. если например цена деления линейки 1мм = 0,1см, то абсолютная погрешность будет с точностью до 0,1 ( ≤ 0,1) и будет определена только оценка относительной погрешности (т.е. ≤ какому числу %).

Если х≈а абсолютная погрешность этого приближенного значения не превосходит некоторого числа h, то число а называют приближенным значением х с точностью до h.
х≈а с точностью до h.

Задача.
Найдем относительную погрешность при измерении длины листа тетради линейками: одна – с точностью до 0,1см (деления через 0,1см); вторая - с точностью до 1см (деления через 1см).
ℓ1 = 20,4см ℓ2 = 20,2см
0,1 : 20,4 = 0,0049 = 0,49% 1 : 20,2 = 0,0495 = 4,95%

Говорят, относительная погрешность в первом случае до 0,49%(т.е ≤ 0,49%), во втором случае до 4,95% (т.е. ≤ 4,95%).
В первом случае точность измерения выше.
Мы говорим не о величине
относительной погрешности, а ее оценке.

Найдите абсолютную и относительную погрешности, полученные в результате округления
а) до десятых 6,56; 0,475; 3,671
б) до десятков 124; 361; 720

На производстве при изготовлении деталей мы пользуемся
штангенциркулем (для измерения глубины; диаметра: наружного и внутреннего).
Абсолютная погрешность при измерении этим прибором составляет точность до 0,1мм. Найдем оценку относительной погрешности при измерении штангенциркулем:
d = 9,86см = 98,6мм
0,1 : │98,6│= 0,1 : 98,6 = 0,001 = 0,1%

Относительная погрешность с точностью до 0,1% (т.е. ≤ 0,1%).
Если сравнить с предыдущими двумя измерениями, то получается точность измерения выше.

Из практических примеров можно сделать вывод, что точных значений быть не может, производя измерения в обычных условиях.
Но чтобы точнее выполнить измерение нужно взять измерительный прибор цена деления которого как можно меньше.

Задача
При измерении длины стержня пользовались линейкой, штангенциркулем, микрометром. При этом были получены результаты 17,9 мм; 18 мм; 17,88 мм. Каким прибором измеряли?

Задача
Найдите абсолютную погрешность, полученную в результате округления
а) до десятых 6,56; 0,475; 3,671
б) до десятков 124; 361; 720

какие из значений величин точные и какие приближенные?
Толщина книги 25 мм
Температура воздуха 18*
В самолете 122 пассажира
Скорость звука в воздухе 322 м/с
Масса дыни 3,5 кг
Стоимость ручки 5 руб.
В тетради начерчен угол 50*
Рекорд соревнований в беге на 1500м равнялся 3мин 56с
Точные
Приближенные