Системы линейных дифференциальных уравнений

Мини-КР
1. Решить ОЛДУ
2. Найти вид частного решения НЛДУ

Введение
Существуют методы решения систем дифференциальных уравнений, сходные с теорией решения ЛДУ.

Основные понятия теории СЛДУ
Определение. Нормальная система ДУ называется линейной, если в каждом ее уравнении функции
линейны относительно неизвестных функций, т. е. если она имеет вид:
Запишем систему в векторной форме:
где
При получим систему ОЛДУ вида

Свойства решений СОЛДУ
Обозначим через Y множество всех решений СОЛДУ, Y – линейное пространство.

Теорема о структуре общего решения СОЛДУ

Теорема о структуре общего решения СНЛДУ
Если 1) - ФСР СОЛДУ
2) – некоторое решение СНЛДУ
то общее решение СНЛДУ находится по формулам:
или
Для поиска частного решения можно воспользоваться методом вариации произвольной постоянной (из СОЛДУ):

СНЛДУ имеет решение
Тогда т.е.
Т.к. то
Отсюда
Проинтегрируем обе части:
t0 – любое число (a,b).
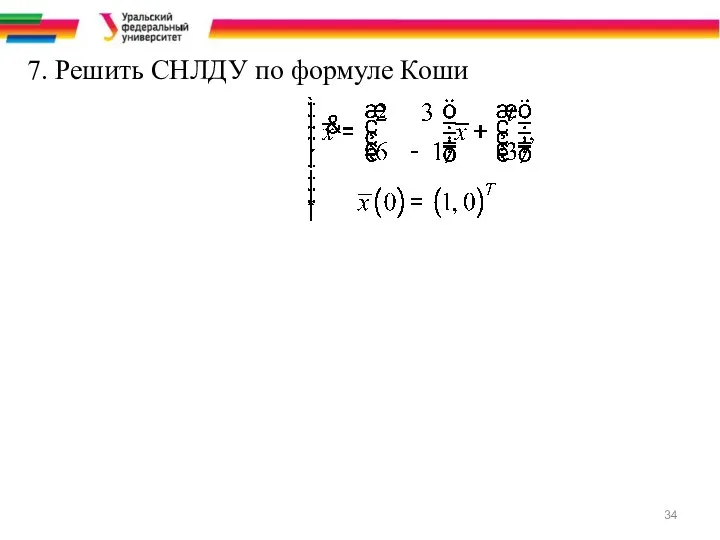
Т.О. - формула Коши.

ОСЛДУ с постоянными коэффициентами

4. Найти общее решение СНЛДУ используя метод Эйлера для СОЛДУ и подбор решений для СНЛДУ

5. Найти общее решение СОЛДУ методом Эйлера

6. Найти общее решение СОЛДУ методом Эйлера

7. Решить СНЛДУ по формуле Коши

Формула Коши