Содержание
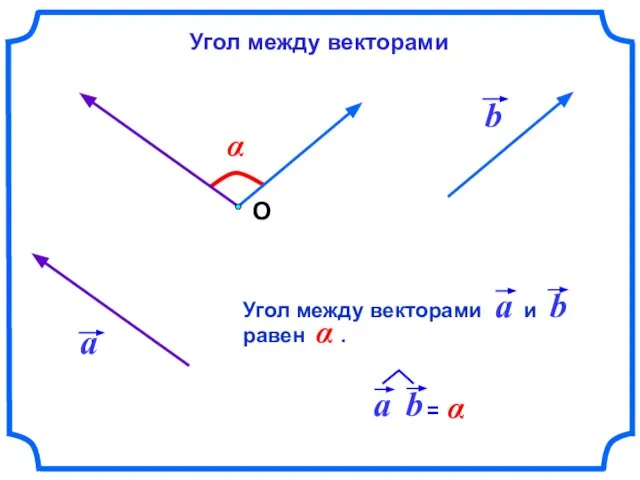
- 2. α О Угол между векторами
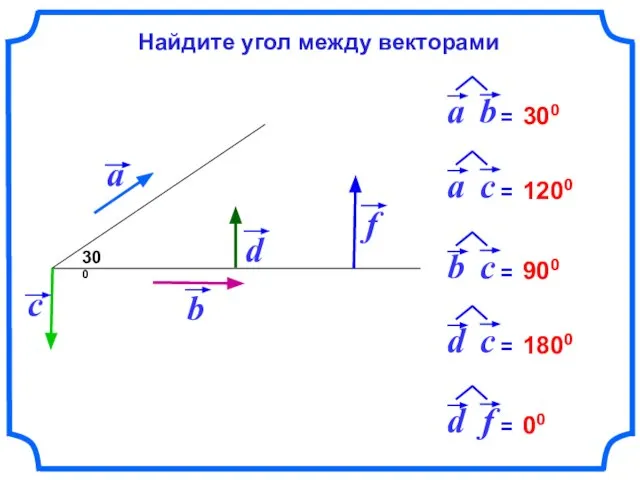
- 3. 300 300 1200 900 1800 00 Найдите угол между векторами
- 4. Критерии оценивания: Умеет определять скалярного произведения векторов в пространстве; Знает свойства скалярного произведения векторов в пространстве;
- 5. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
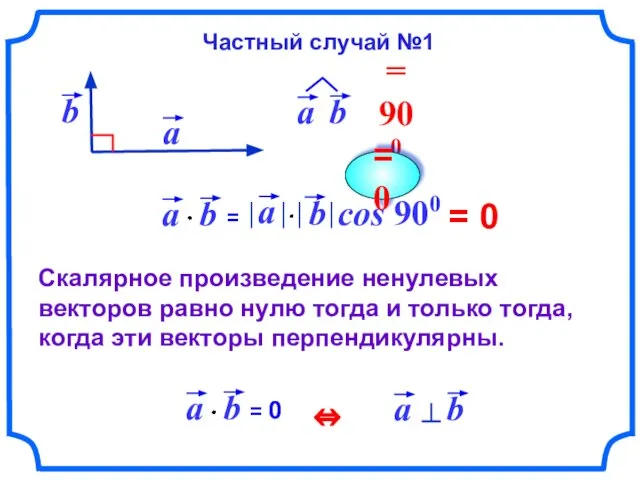
- 6. = 0 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
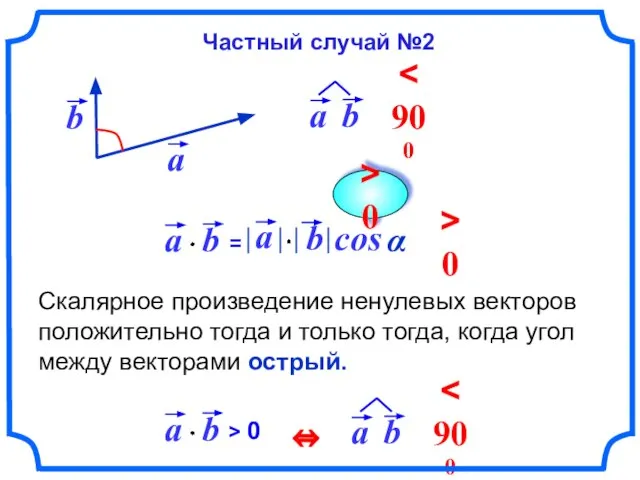
- 7. Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. cos α
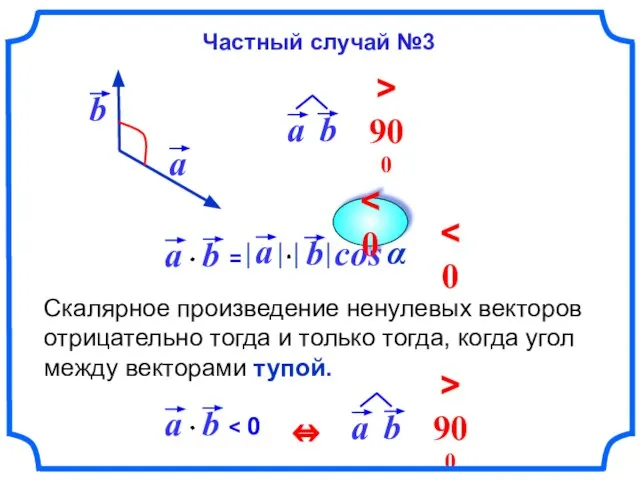
- 8. Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. cos α
- 9. cos 00 1 cos1800 -1 Частный случай №4
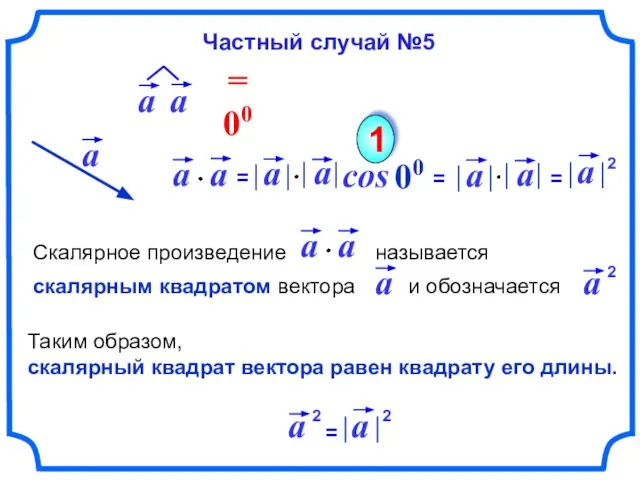
- 10. cos 00 1 Таким образом, скалярный квадрат вектора равен квадрату его длины. Частный случай №5 2
- 11. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2 + z1z2
- 12. Пример №1 Найти скалярное произведение векторов: a {-6; 9; 5} b {-1; 0; 7}
- 13. Пример №3 Найти скалярное произведение векторов: a {1; 7; 9} b {-2; 4; 0}
- 15. Скачать презентацию






 Задача на арифметическую прогрессию (1)
Задача на арифметическую прогрессию (1) Логический элемент
Логический элемент Тригонометрические уравнения
Тригонометрические уравнения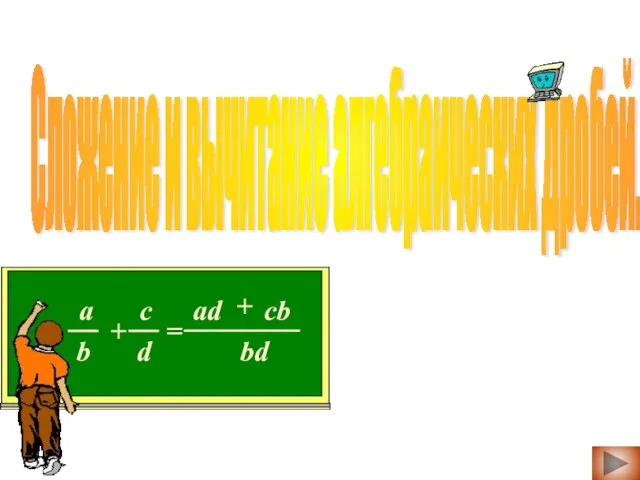 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Основные задачи и область применения дискретной математики
Основные задачи и область применения дискретной математики Симетричні фігури
Симетричні фігури Лекция 5. Плоские и планарные графы
Лекция 5. Плоские и планарные графы Презентация на тему Объем прямой призмы
Презентация на тему Объем прямой призмы  Стереометрия. 1
Стереометрия. 1 Сравнение чисел
Сравнение чисел Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Решение задач
Решение задач Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Больше, меньше, столько же
Больше, меньше, столько же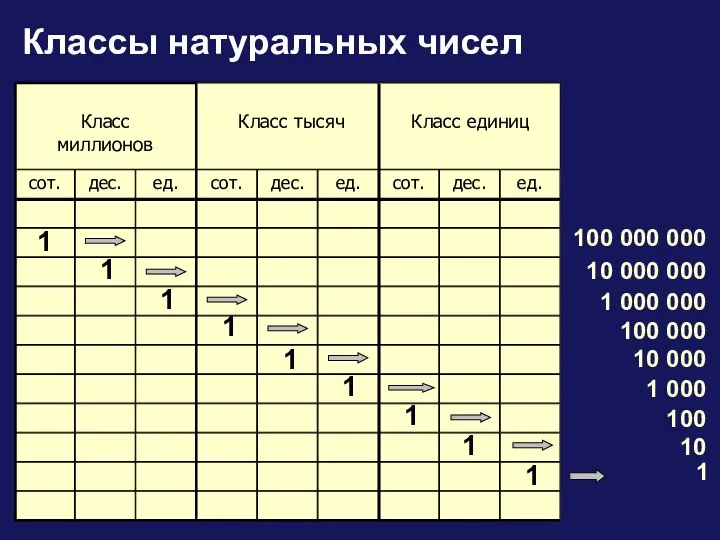 Классы натуральных чисел
Классы натуральных чисел Исследование функции на монотонность
Исследование функции на монотонность Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Элементы комбинаторики
Элементы комбинаторики Сложение с переходом через десяток
Сложение с переходом через десяток Сумма n первых членов геометрической прогрессии (9 класс)
Сумма n первых членов геометрической прогрессии (9 класс) Действия с десятичными дробями
Действия с десятичными дробями Показательные уравнения и неравенства
Показательные уравнения и неравенства Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Математический хоккей
Математический хоккей Арифметический корень натуральной степени
Арифметический корень натуральной степени Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств