Содержание
- 2. Немного истории Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми
- 3. Для графического решения квадратного уравнения представьте его в одном из видов: ax2 + bx +c =
- 4. Алгоритм графического решения квадратных уравнений Ввести функцию f(x), равную левой части и g(x) , равную правой
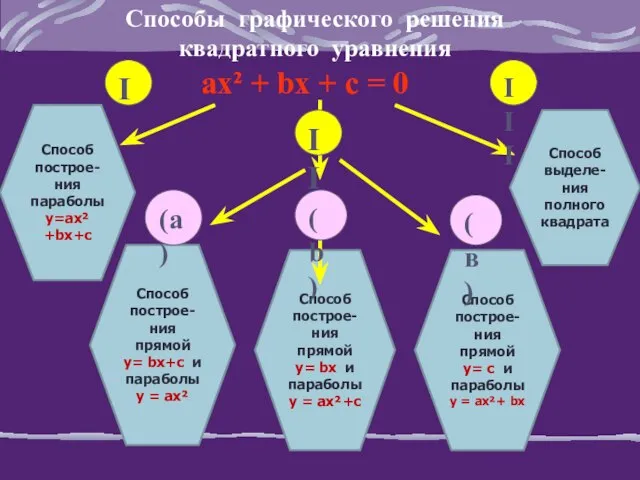
- 5. Способы графического решения квадратного уравнения ах² + bх + с = 0 Способ поcтрое- ния параболы
- 6. «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре
- 7. Графическое решение квадратного уравнения Иллюстрация на одном примере
- 8. Алгоритм решения квадратного уравнения графическим способом Способ 1 Построить график функции y=ax2+bx+c Найти точки пересечения графика
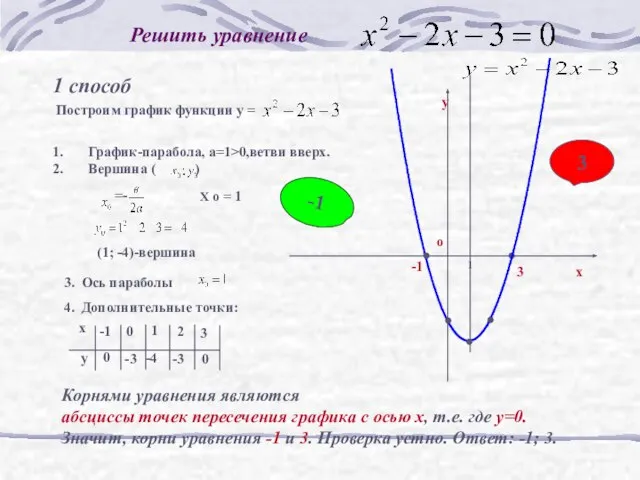
- 9. Решить уравнение 1 способ Корнями уравнения являются абсциссы точек пересечения графика с осью х, т.е. где
- 10. Алгоритм построения параболы найти координаты вершины; провести ось параболы; отметить на оси абсцисс две точки, симметричные
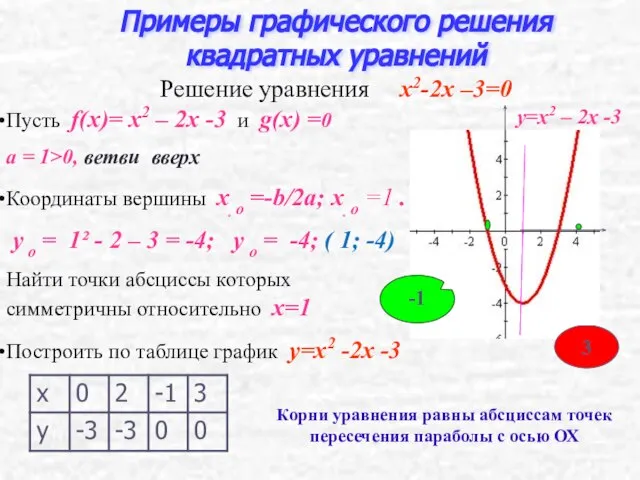
- 11. Пусть f(x)= x2 – 2x -3 и g(x) =0 а = 1>0, ветви вверх Координаты вершины
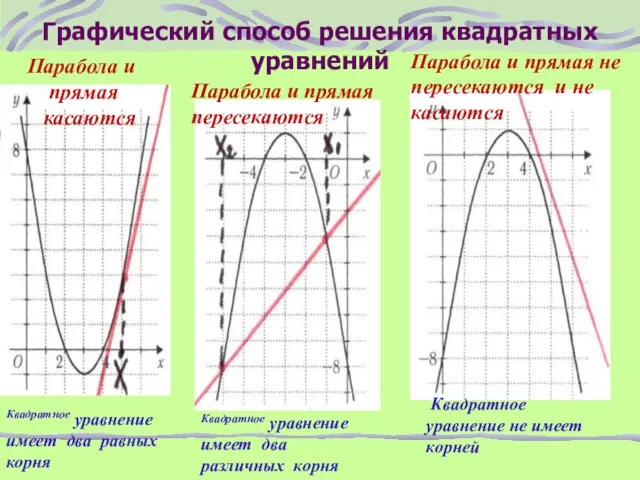
- 12. Графический способ решения квадратных уравнений Парабола и прямая касаются Парабола и прямая пересекаются Квадратное уравнение имеет
- 13. Алгоритм решения квадратного уравнения графическим способом Способ 2(а) Построить графики функции y=ax2 и у = bx+
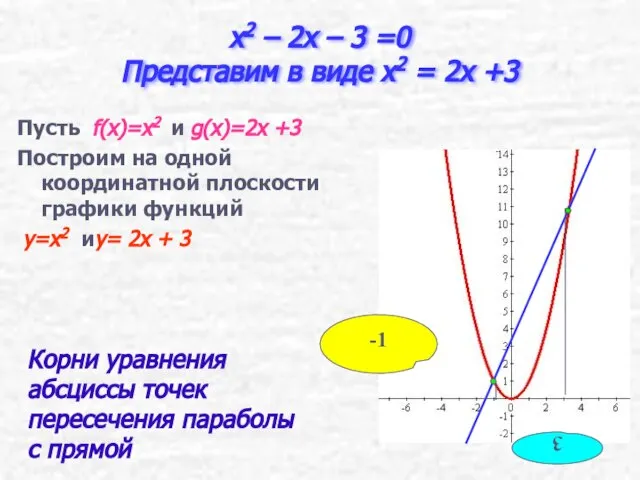
- 14. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и
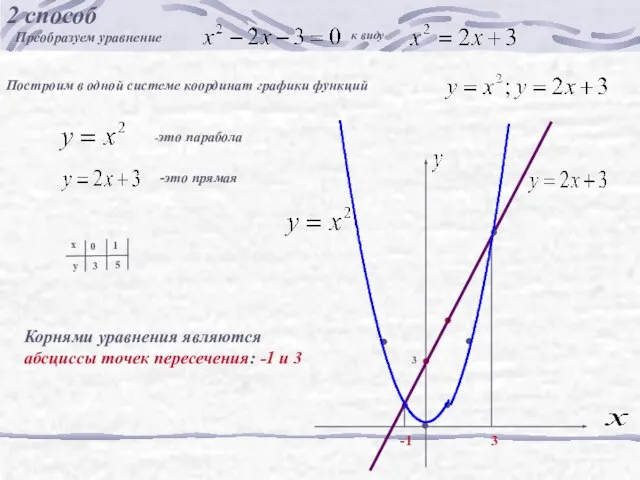
- 15. 2 способ Преобразуем уравнение к виду Построим в одной системе координат графики функций -это парабола -это
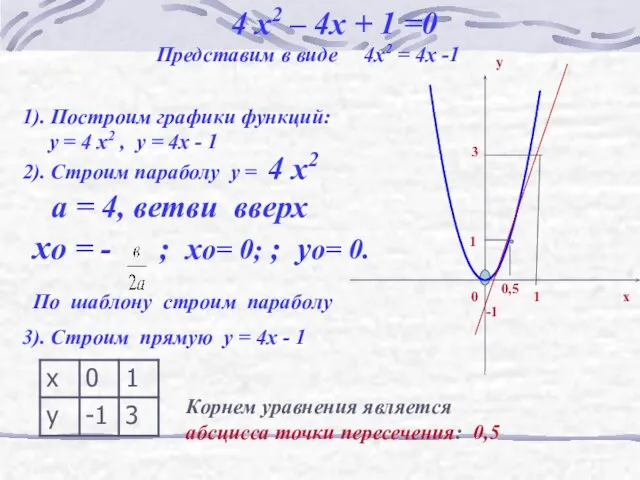
- 16. 4 x2 – 4x + 1 =0 Представим в виде 4x2 = 4x -1 1). Построим
- 17. Алгоритм решения квадратного уравнения графическим способом Способ 2 (b) Преобразовать уравнение к виду ax2+с = bx
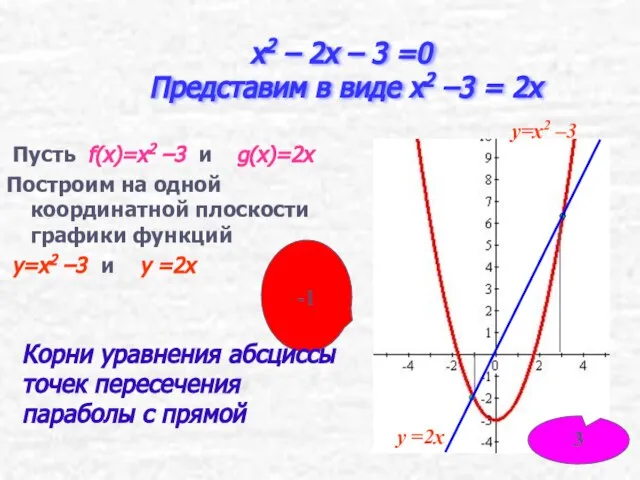
- 18. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3
- 19. x2 – 4x + 5 =0 Представим в виде x2 +5 = 4x Пусть f(x)=x2 +5
- 20. Алгоритм решения квадратного уравнения графическим способом Способ 2(в) Построить графики функции y=ax2 + bx и у
- 21. x2 – 2x – 3 =0 Представим в виде x2 – 2x = 3 Пусть f(x)=
- 22. Алгоритм решения квадратного уравнения графическим способом Способ 3 (выделение полного квадрата) Преобразовать уравнение к виду a(x+l)2
- 23. Выделение квадрата двучлена. x2 – 2x + 1 = 3 + 1 ( x –1)2=4. x2
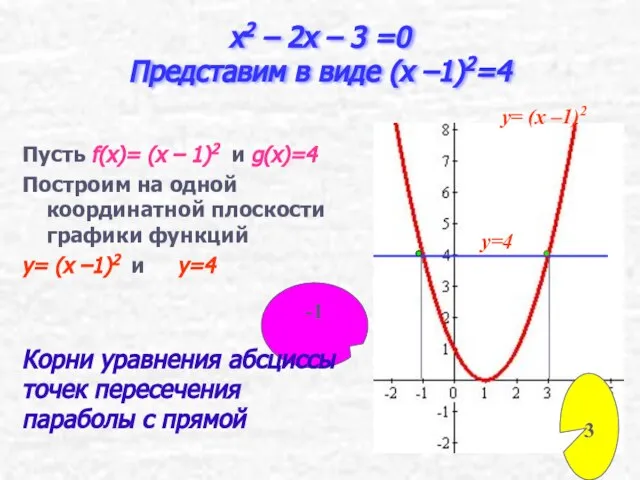
- 24. x2 – 2x – 3 =0 Представим в виде (x –1)2=4 Пусть f(x)= (x – 1)2
- 25. Решите графически уравнение Группа А Бычев Андрей Ерофеева Ксения Каминская Света Лобов Егор Лукьяненко Вероника Осипов
- 26. Сколько нам открытий чудных готовит просвещения дух?
- 27. Решить графически уравнение
- 28. Как решить уравнение? Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут
- 29. Решить графически уравнение
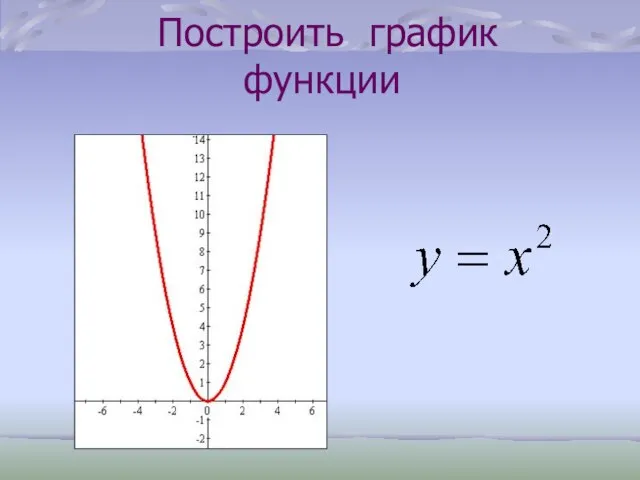
- 30. Построить график функции
- 31. Построить график функции
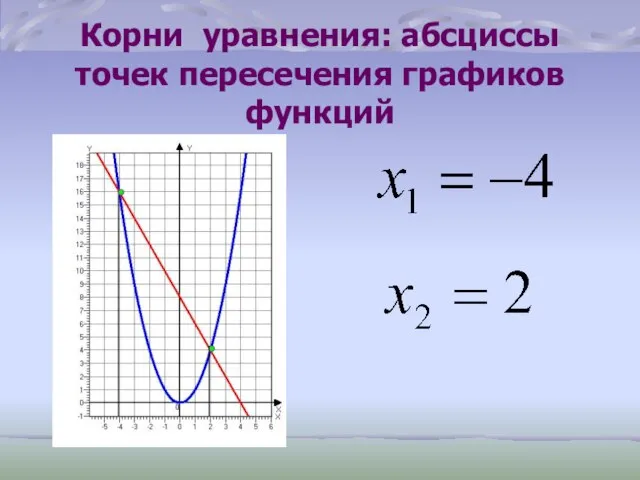
- 32. Корни уравнения: абсциссы точек пересечения графиков функций
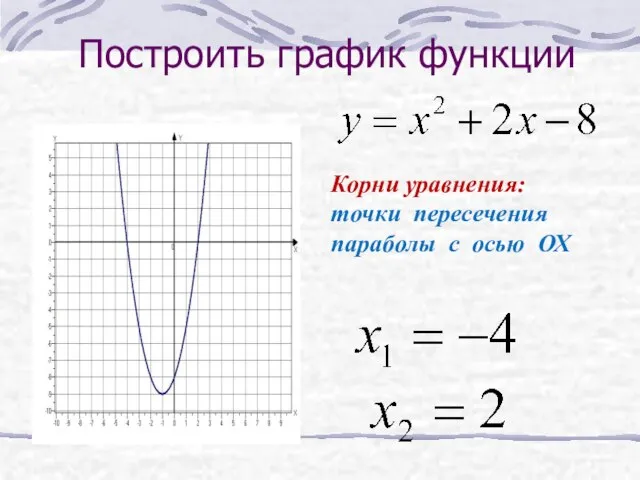
- 33. Построить график функции Корни уравнения: точки пересечения параболы с осью ОХ
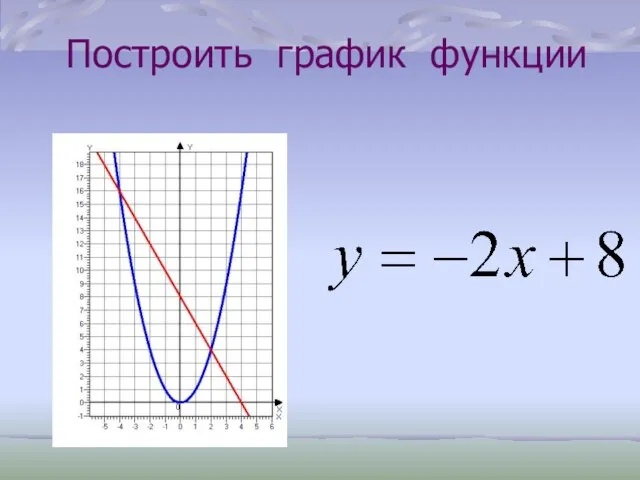
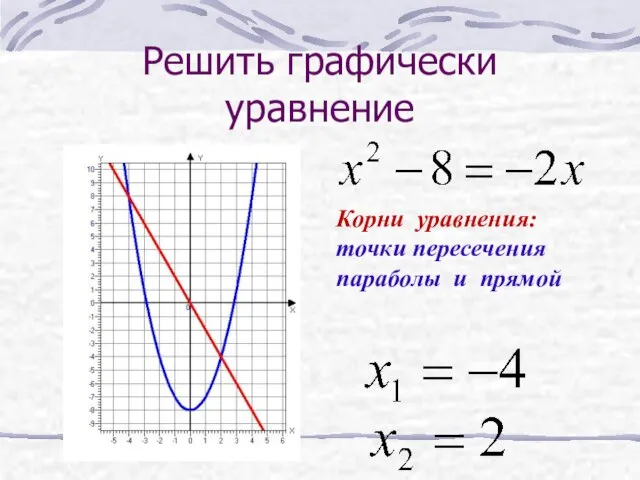
- 34. Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
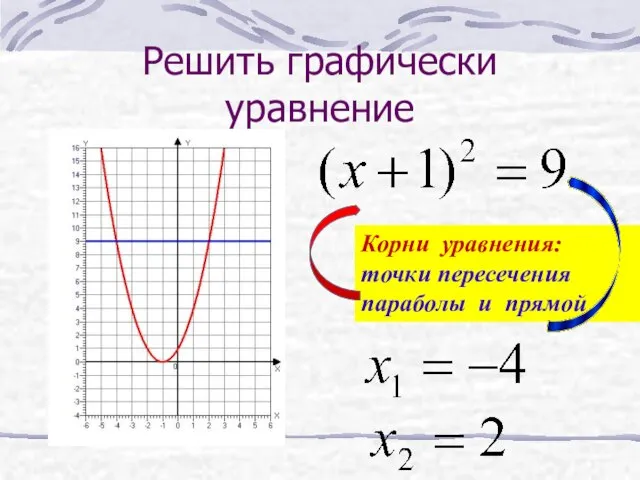
- 35. Решить графически уравнение Корни уравнения: точки пересечения параболы и прямой
- 36. Итог Познакомились: с графическим методом решения квадратных уравнений; с различными способами графического решения квадратных уравнений. закрепили
- 37. Заключительное слово учителя: «Чем больше и глубже вам удастся усвоить азы математики и научиться пользоваться ее
- 39. Скачать презентацию




















 Тренинговая работа №3
Тренинговая работа №3 Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Треугольник и его виды
Треугольник и его виды Урок – игра «В мире числительных»
Урок – игра «В мире числительных» Семь чудес света: математика 1 класс
Семь чудес света: математика 1 класс Перпендикулярность прямой и плоскости. Решение задач
Перпендикулярность прямой и плоскости. Решение задач Повторение по математике
Повторение по математике Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт
Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт Элементы комбинаторики
Элементы комбинаторики Математика. Фигуры
Математика. Фигуры Теория графов
Теория графов ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум
ризнаки монотонности функции. Экстремум функции. Исследование функции на монотонность и экстремум Измерение углов. Транспортир
Измерение углов. Транспортир Решение задач на разностное и кратное сравнение
Решение задач на разностное и кратное сравнение Расстояние между двумя точками. 9 класс
Расстояние между двумя точками. 9 класс Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Ладога в цифрах
Ладога в цифрах Создание системы внеклассной работы в физико-математическом образовании
Создание системы внеклассной работы в физико-математическом образовании Возведение в квадрат суммы трех, четырех и более слагаемых
Возведение в квадрат суммы трех, четырех и более слагаемых Numbers and animals
Numbers and animals Деление многочленов
Деление многочленов Конкретный смысл действия деления
Конкретный смысл действия деления Логарифмическая функция
Логарифмическая функция Что мы знаем о иррациональности
Что мы знаем о иррациональности Математика.Задачки. (тест)
Математика.Задачки. (тест) Презентация на тему Итоговый зачет по математике (6 класс)
Презентация на тему Итоговый зачет по математике (6 класс)  Расстояния и углы
Расстояния и углы Различные способы доказательств в курсе геометрии
Различные способы доказательств в курсе геометрии