Содержание
- 2. Математика и ее роль в жизни общества
- 3. Небольшое вступление о необходимости изучения математики Математика – это наука о количественных отношениях и пространственных формах
- 4. Часто студенты задают мне именно такие вопросы: А для чего нужна математика? Для чего мы учим
- 5. Думаю, что все вы нашли для себя ответы на эти вопросы. Вот некоторые из них: Математика
- 6. При выполнении домашней контрольной работы, вы уже изучили такие темы, как «Понятие геометрической величины» «Понятие скалярной
- 7. основатель теории множеств Георг Кантор «Множество есть многое, мыслимое нами как единое»
- 8. Понятия теории множеств Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно
- 9. Придумайте название для предметов и животных, собранных вместе: КОЛЛЕКЦИЯ МАРОК НАБОР КАРАНДАШЕЙ СТАЯ ПТИЦ ЧАЙНЫЙ СЕРВИЗ
- 10. И это все множества. Придумайте устно еще примеры множеств.
- 11. Множество – совокупность объектов, объединенных по какому – нибудь признаку. Объекты, составляющие множество, называются элементами множества.
- 12. Например, на рисунке изображено множество четырехугольников. А элементами являются все четырехугольники: трапеция, прямоугольник, квадрат, параллелограмм, ромб.
- 13. На следующем слайде вам будет представлена таблица, которую вы должны заполнить. Постарайтесь выполнить это задание сами,
- 14. Множество четырехугольников Пространственные тела 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… Квадраты
- 15. Как видите, математика построена именно на понятии множества, хотя в школе вы может и не встречали
- 16. и так Обозначения некоторых числовых множеств: N – множество натуральных чисел; Z – множество целых чисел;
- 17. Стандартные обозначения В математике нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Для
- 18. Принадлежность элемента множеству можно записать символически и прочитать: , «элемент (объект) а принадлежит множеству А» или
- 19. Стандартные обозначения
- 20. Прочитайте высказывания и укажите среди них верные (из видео урока вы узнали о числовых множествах)
- 21. Рассмотрим ВИДЫ МНОЖЕСТВ
- 22. А = {2; 3; 5; 7; 11; 13}; Множество состоит из таких элементов х, что х
- 23. {1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …}; Здесь мы не можем
- 24. 1. Множество людей на Солнце 2.Множество прямых углов равностороннего треугольника 3. Множество точек пересечения двух параллельных
- 25. Среди перечисленных ниже множеств укажите конечные и бесконечные множества: а) множество чисел, кратных 13; б) множество
- 26. Способы задания множеств Перечислить все его элементы Указать характеристическое свойство Характерестическое свойство – это такое свойство,
- 27. Задача 1. Запишите натуральные числа, которые больше, чем 25 и меньше, чем 30. Решение. Множество чисел
- 28. Задача 2. Укажите характеристическое свойство элементов множества Решение. Множество чисел задано перечислением его элементов. Их характеристическое
- 29. 1. Задайте множество цифр, с помощью которых записывается число: а) 3254; б) 8797; в) 11000; г)
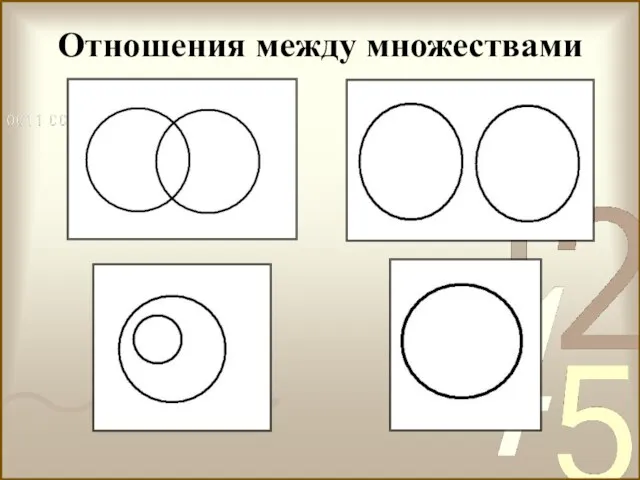
- 30. Отношения между множествами
- 31. Отношения между множествами Если множества А и В имеют некоторые общие элементы, то говорят, что эти
- 32. Что бы было наглядно видно эти отношения, их можно изобразить с помощью кругов, которые называются кругами
- 33. Отношения между множествами
- 34. В каких отношениях находятся множества
- 35. Ответы А и В пересекаются, есть общие элементы в,d; А и С не пересекаются, нет общих
- 36. В и D пересекаются, общий элемент d; Ви Е равные, элементы совпадают; С и D не
- 37. Занятие 2. Операции над множествами
- 38. Над числами в математике можно производить операции (сложение, вычитание, умножение, деление), так и над множествами можно
- 39. Теперь запишите все определения, сделайте геометрическую иллюстрацию и примеры на все операции.
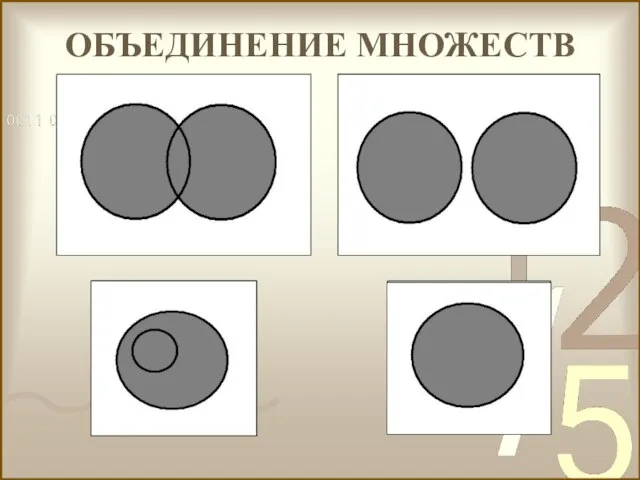
- 40. Суммой или объединением произвольного конечного или бесконечного множества называется множество, состоящее из тех и только тех
- 41. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
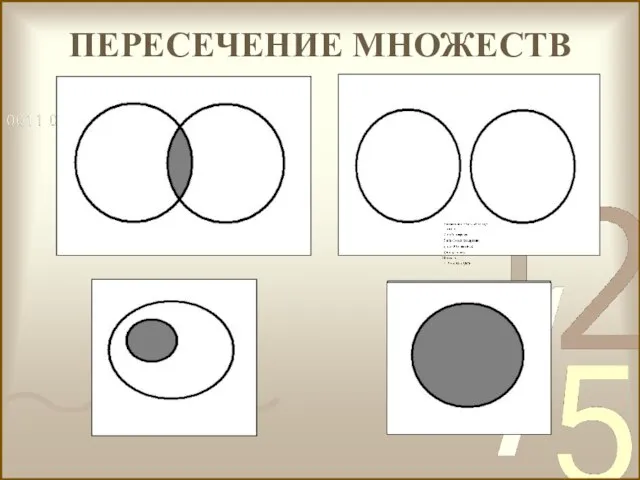
- 42. Пересечением любого конечного или бесконечного множества называется множество, состоящее из тех и только тех элементов, которые
- 43. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
- 44. Разностью множеств Х и У называется множество, содержащее все элементы, которые принадлежат множеству Х и не
- 46. Скачать презентацию








































 Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Решение задач. Самостоятельная работа (ЕГЭ)
Решение задач. Самостоятельная работа (ЕГЭ) Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Метод координат на плоскости
Метод координат на плоскости Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Задание 19. Профиль (1)
Задание 19. Профиль (1) Переменные величины и их свойства
Переменные величины и их свойства Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена
Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена  Динамическое программирование
Динамическое программирование Задачи на нахождение неизвестного
Задачи на нахождение неизвестного Решаем задачу
Решаем задачу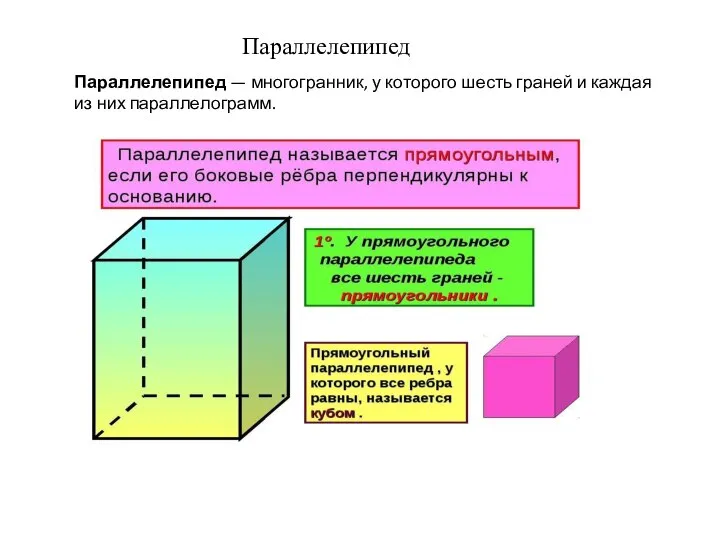 Параллелепипед
Параллелепипед Пирамида
Пирамида Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Число и цифра 6. 1 класс
Число и цифра 6. 1 класс Задания 15 и 4
Задания 15 и 4 Прямой угол
Прямой угол Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Функции, их свойства и графики
Функции, их свойства и графики Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Уравнение сферы
Уравнение сферы Геометрический и физический смысл производной
Геометрический и физический смысл производной Площадь параллелограмма
Площадь параллелограмма Изображение фигур в пространстве
Изображение фигур в пространстве Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем