Стереометрия. Теория

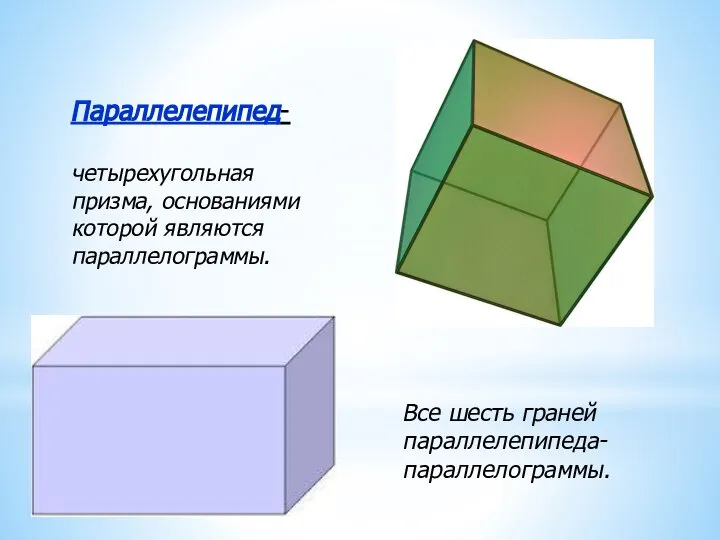
Параллелепипед-
четырехугольная призма, основаниями которой являются параллелограммы.
Все шесть граней параллелепипеда- параллелограммы.

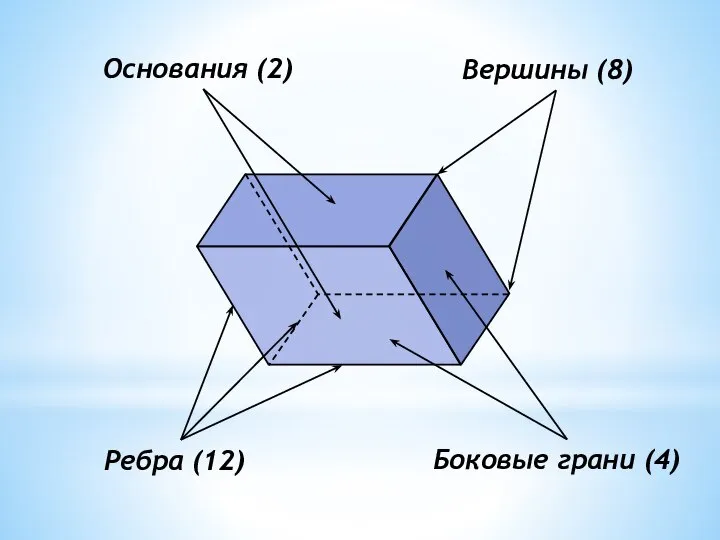
Ребра (12)
Боковые грани (4)
Вершины (8)
Основания (2)

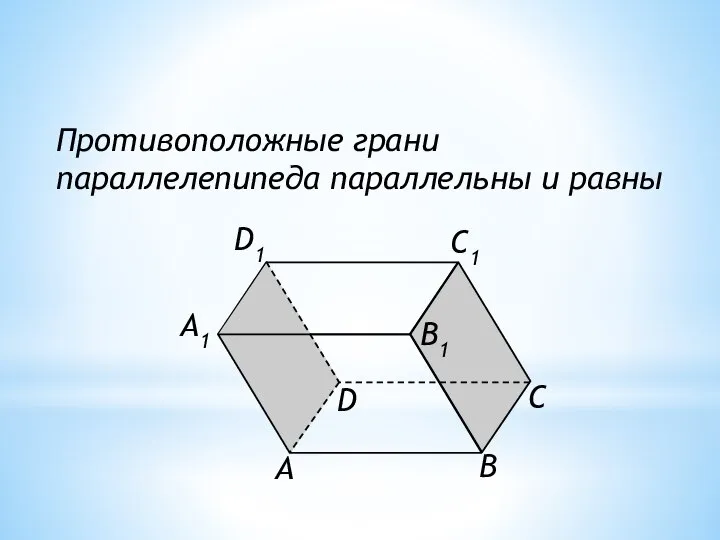
А
В
С
А1
D
D1
B1
C1
Противоположные грани параллелепипеда параллельны и равны

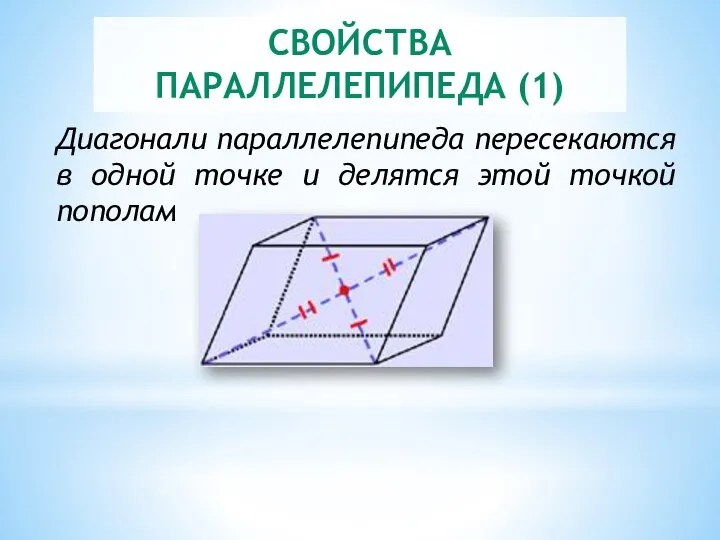
СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (1)
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

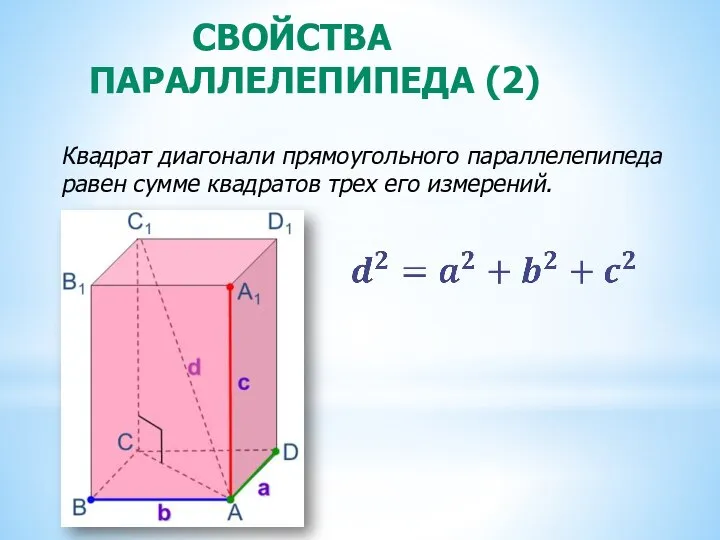
СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (2)
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

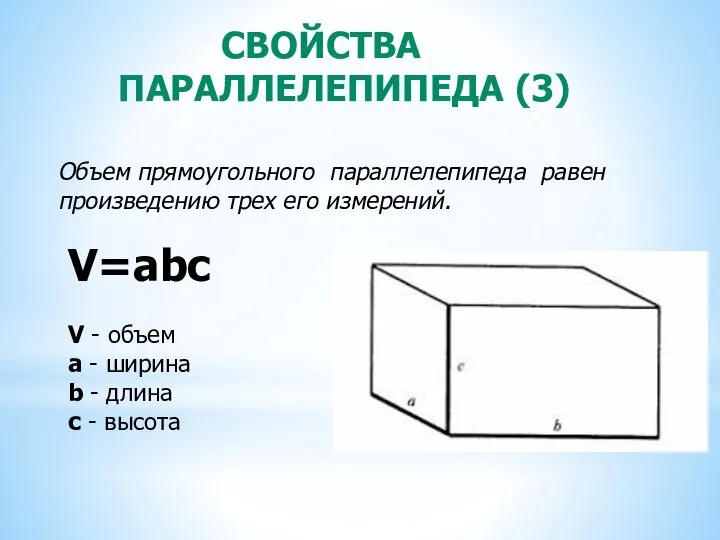
СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (3)
Объем прямоугольного параллелепипеда равен произведению трех его измерений.
V=abc
V - объем
a - ширина
b - длина
c - высота

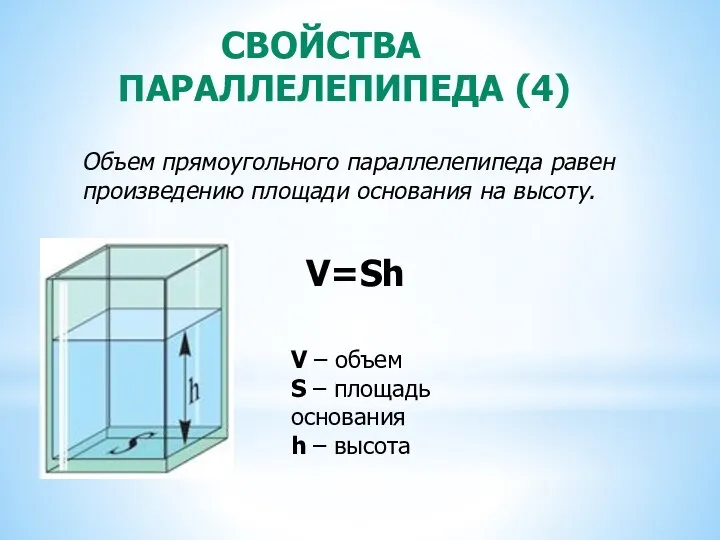
СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА (4)
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
V=Sh
V – объем
S – площадь основания
h – высота

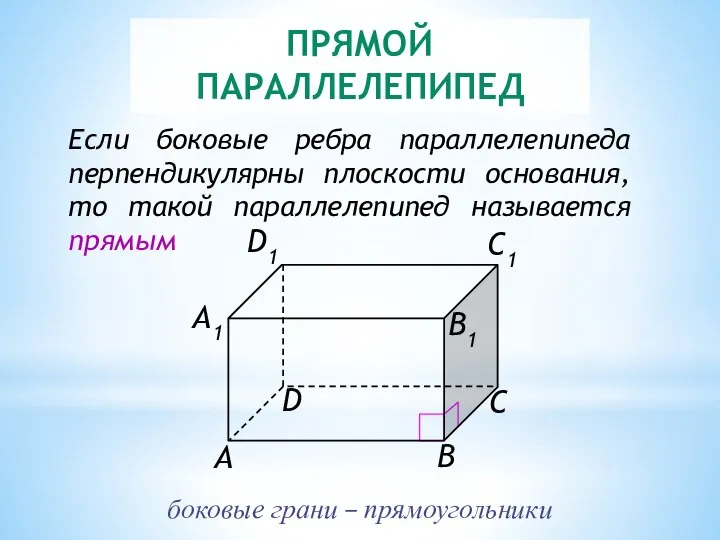
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед называется прямым
боковые грани – прямоугольники

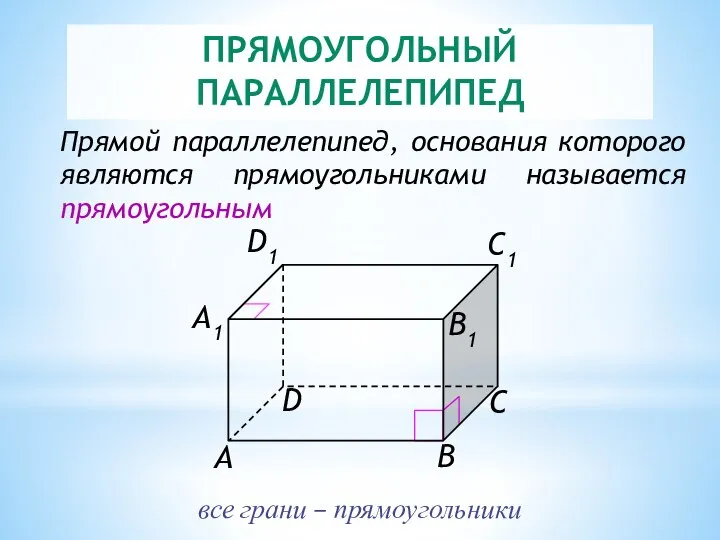
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным
все грани – прямоугольники

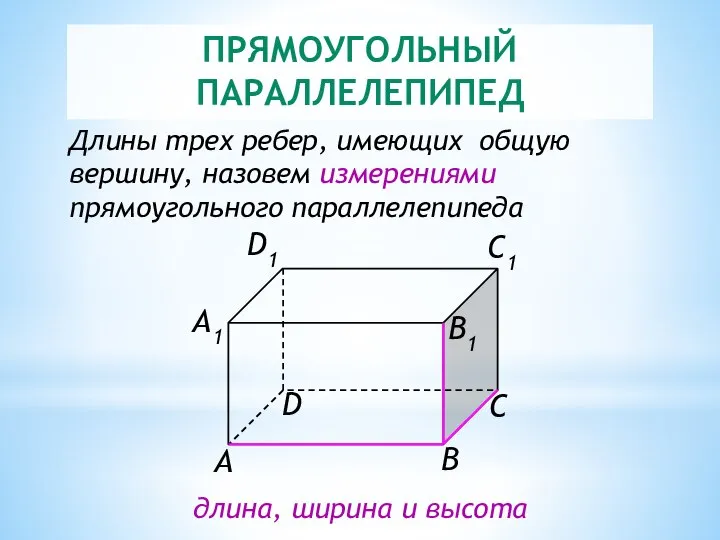
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД
Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда
длина, ширина и высота

Площадь поверхности
а
b
c
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда.

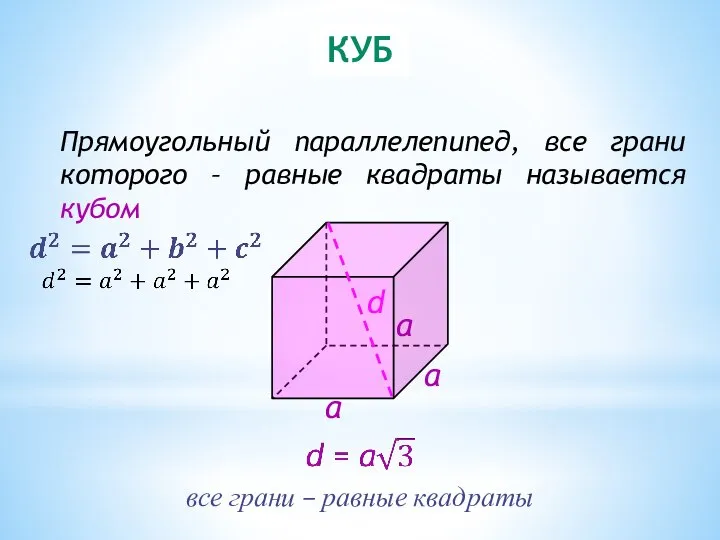
КУБ
Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом
все грани – равные квадраты
d
a
a
a

Задачи
Площадь поверхности куба равна 18. Найдите его диагональ.
Объем куба равен 8. Найдите площадь его поверхности.
Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Объемы подобных тел относятся как куб коэффициента подобия.
Площади поверхностей подобных тел относятся как квадрат коэффициента подобия.

Задачи
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.

Определение призмы:
Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.

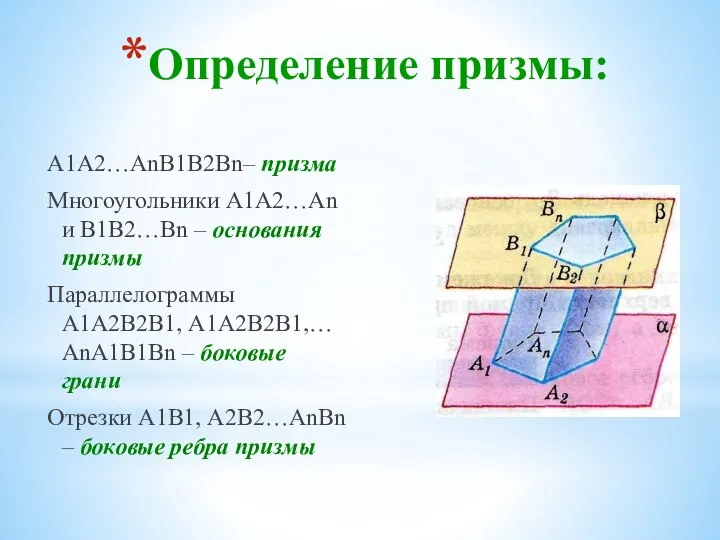
Определение призмы:
А1А2…АnВ1В2Вn– призма
Многоугольники А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы

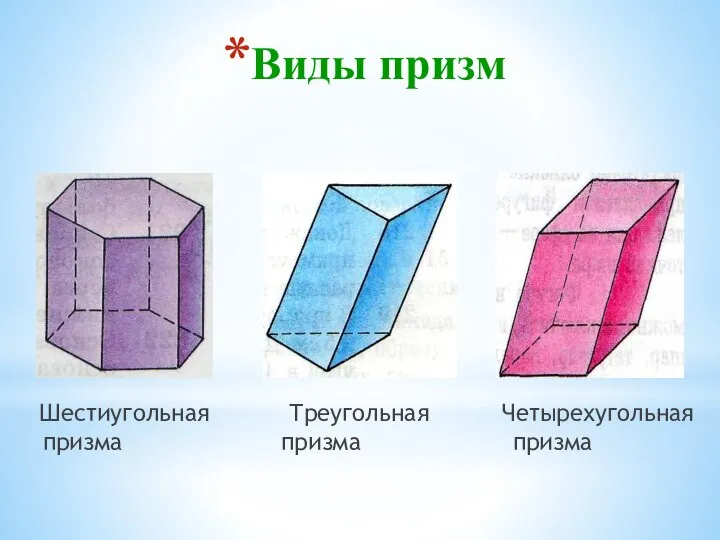
Виды призм
Шестиугольная Треугольная Четырехугольная призма призма призма

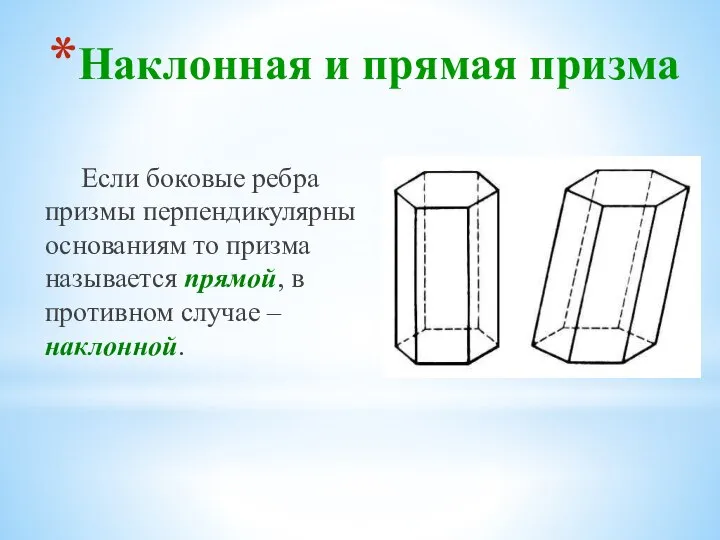
Наклонная и прямая призма
Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном случае – наклонной.

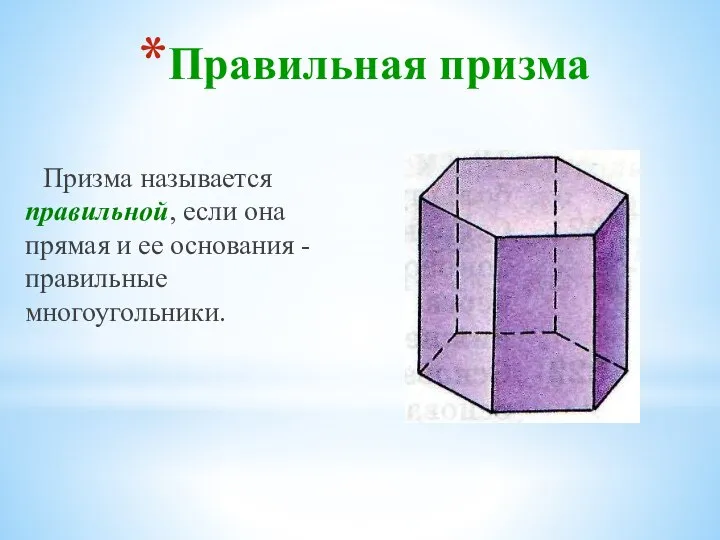
Правильная призма
Призма называется правильной, если она прямая и ее основания - правильные многоугольники.

Площадь полной поверхности призмы

Площадь боковой поверхности призмы
Теорема
Площадь боковой поверхности прямой призмы равна половине произведения периметра основания на высоту призмы.

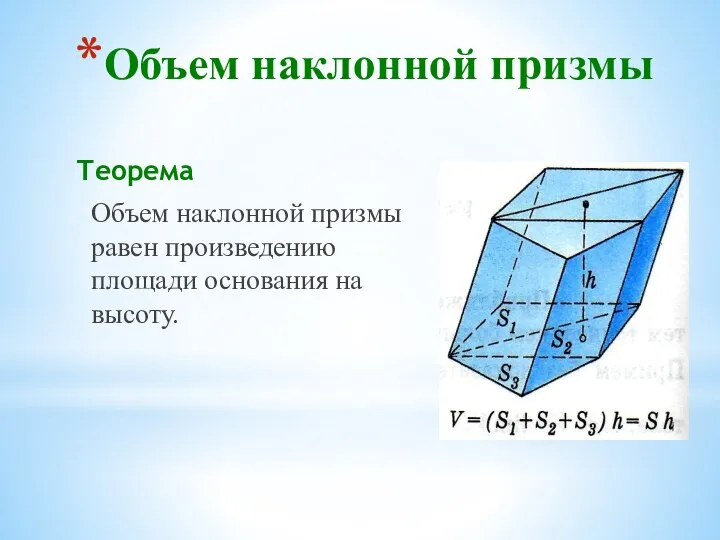
Объем наклонной призмы
Теорема
Объем наклонной призмы равен произведению площади основания на высоту.

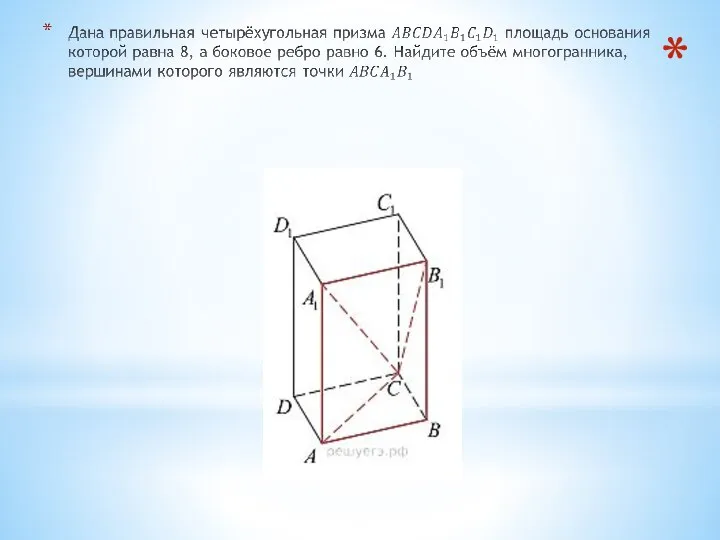
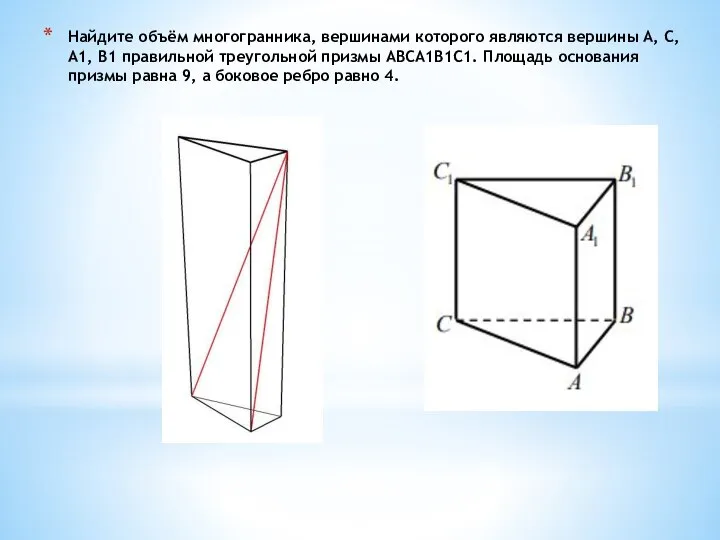
Найдите объём многогранника, вершинами которого являются вершины A, C, A1, B1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 9, а боковое ребро равно 4.