Содержание
- 3. Логарифмирование алгебраических выражений Если число х представлено алгебраическим выражением, то логарифм любого выражения можно выразить через
- 4. Прологарифмируем выражение по основанию 2 (Выразим его через ) Решение:
- 5. Потенцирование логарифмических выражений Переход от логарифмического выражения к алгебраическому называется потенцированием, то есть, произвести действие, обратное
- 6. Найти х: lg x = lg a + 2lg b – lg c lg x =
- 7. Найдём х, если -
- 8. Найти значение выражения
- 9. А теперь попробуйте сами…
- 17. Скачать презентацию












 Комбинаторика
Комбинаторика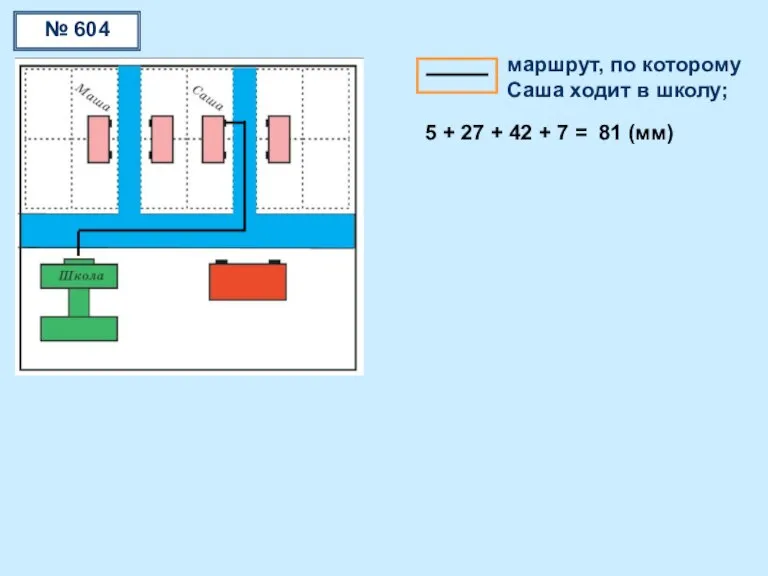 Задачи на расстояние
Задачи на расстояние Сумма углов треугольника
Сумма углов треугольника Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Обеспечивающие подсистемы АИС. Математическое обеспечение
Обеспечивающие подсистемы АИС. Математическое обеспечение Маршрутный лист группы
Маршрутный лист группы Математика в лицах
Математика в лицах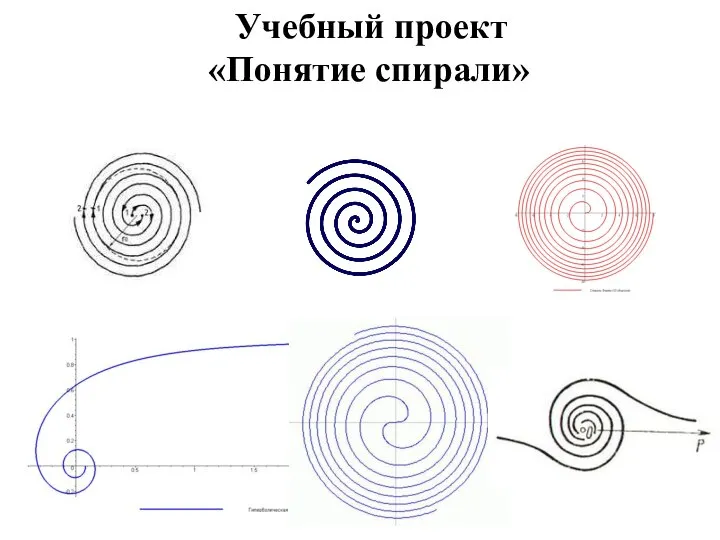 Понятие спирали
Понятие спирали Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів Презентация на тему Софизмы и парадоксы
Презентация на тему Софизмы и парадоксы  Математический дизайн
Математический дизайн Золотое сечение - божественная мера красоты
Золотое сечение - божественная мера красоты Части задачи
Части задачи Блиц-опрос
Блиц-опрос Аналитические функции и конформные отображения
Аналитические функции и конформные отображения Нахождение корней уравнения с помощью подбора параметра
Нахождение корней уравнения с помощью подбора параметра Презентация на тему Повторение курса начальной школы в 5-м классе
Презентация на тему Повторение курса начальной школы в 5-м классе  Презентация на тему Танграм
Презентация на тему Танграм  Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (5 класс)  Стереометрия. Теория
Стереометрия. Теория Равносильные формулы. Уроки 17-18
Равносильные формулы. Уроки 17-18 Деление дробей
Деление дробей Подготовка к ПА. Математика
Подготовка к ПА. Математика Чётные и нечётные числа. Подготовка к контрольной работе
Чётные и нечётные числа. Подготовка к контрольной работе Решение уравнений
Решение уравнений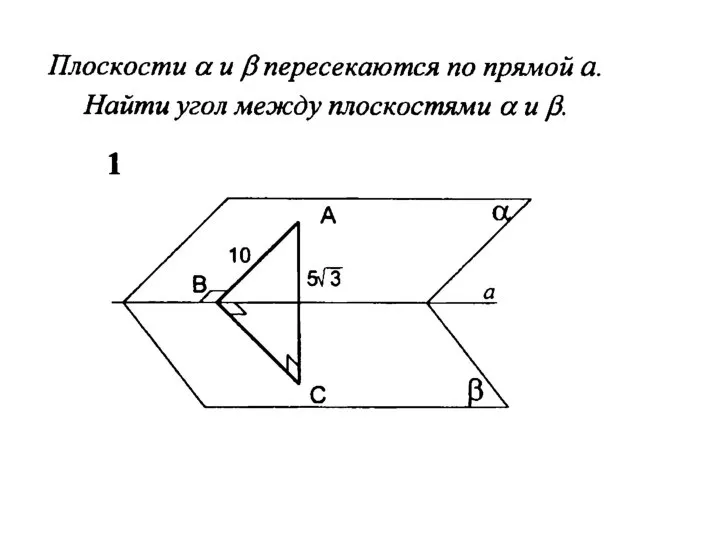 Угол между плоскостями
Угол между плоскостями Математические методы в экономике. Лекция 8
Математические методы в экономике. Лекция 8 Подобие. Коэффициент подобия
Подобие. Коэффициент подобия