Задачи на смеси и сплавы

РЕШЕНИЕ:
(от большего , естественно, отнимаем меньшее)
задача

задача1
Объемы искомых растворов относятся как
Т.е. 2 части первого и 3 части второго раствора
2х +3х = 100
х = 20. 20л приходится на одну часть. Значит, первого раствора надо взять 40 л, а второго 60 л.
Ответ: 40 л и 60 л
1. Один раствор содержит 20% кислот, а второй - 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислот?
1 способ

задача1
Значит, первого раствора надо взять 40 л, а второго 60 л.
Ответ: 40 л и 60 л
1. Один раствор содержит 20% кислот, а второй - 70% кислот. Сколько литров первого и второго раствора нужно взять, чтобы получить 100 л раствора с 50% содержанием кислот?
2 способ
+
=
х л
100-х л
100 л
20%
70%
50%
20х + 70 (100-х) = 50*100
20х + 7000 – 70х = 5000 -50х = -2000
х = 40
20%

40х + 48y = 42(х + у)
40х + 48у = 42х + 42у
40х - 42х = 42у - 48у
2х = - 6у
x=3y
Ответ : в отношении 3 : 1
2. При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 48%, получился раствор с концентрацией 42%. В каком отношении были взяты оба раствора?
40%
48%
42%
х
у
х + у
2 способ
1 способ
задача2
+
=

3 способ
0,4х + 0,48y = 0,42(х + у)
0,4х + 0,48у = 0,42х + 0,42у
0,4х - 0,42х = 0,42у - 0,48у
0,02х = - 0,06у
Ответ : в отношении 3 : 1
2. При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли,концентрация которого 48%, получился раствор с концентрацией 42%. В каком отношении были взяты оба раствора?
задача2

задача3
х = 4у
Ответ: 4 : 1
3. Имеются два сплава с разным содержанием золота. В первом сплаве содержится 35 %, во втором - 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить новый сплав, содержащий 40% золота
1 способ
+
=
х
y
(х + у)
35%
60%
40%
35х + 60у = 40*(х+у)
35х + 60у = 40х +40у 35х-40х = 40у – 60у
- 5х = - 20у
х : у = 4 : 1

задача3
х = 4у
Ответ: 4 : 1
3. Имеются два сплава с разным содержанием золота. В первом сплаве содержится 35 %, во втором - 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить новый сплав, содержащий 40% золота.
2 способ
0,35х + 0,6у = 0,4(х+у)
0,35х + 0,6у = 0,4х +0,4у 0,35х-0,4х = 0,4у – 0,6у
-0,05х = - 0,2у
Пусть х – масса 1 сплава, а у – масса 2 сплава. Количество золота в 1 сплаве 0,35х, а 0,6у – во втором сплаве. Масса нового сплава (х +у), а количество золота в нем 0,4(х +у)

4. Сколько воды надо добавить в 1 л раствора, содержащего 96% спирта, чтобы получить раствор с содержанием спирта 40 %?
1способ 1 л раствора, в котором содержится 96% спирта содержит этого спирта 1* 0,96=0,96 л. Это же количество спирта должны содержать и х л раствора с содержанием спирта 40%.
Следовательно, 0,96= х *0,4, х=2,4 л, и надо добавить
2,4 – 1 = 1,4 л. Ответ: 1,4 л.
2способ
1 л х л х+1 л 96*1+0*х=40(х+1)
96=40х+40
40х=96-40
40х=56
Спирт + вода = раствор х=1,4
Ответ: 1,4 л.
задача4
96%
0%
40%

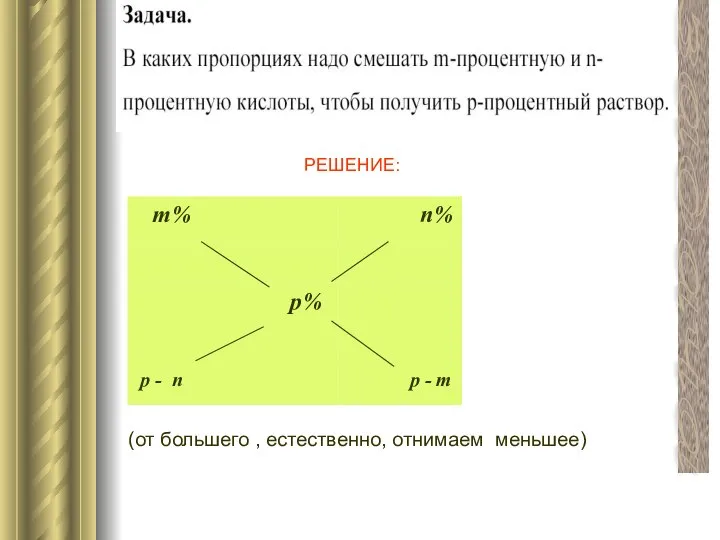
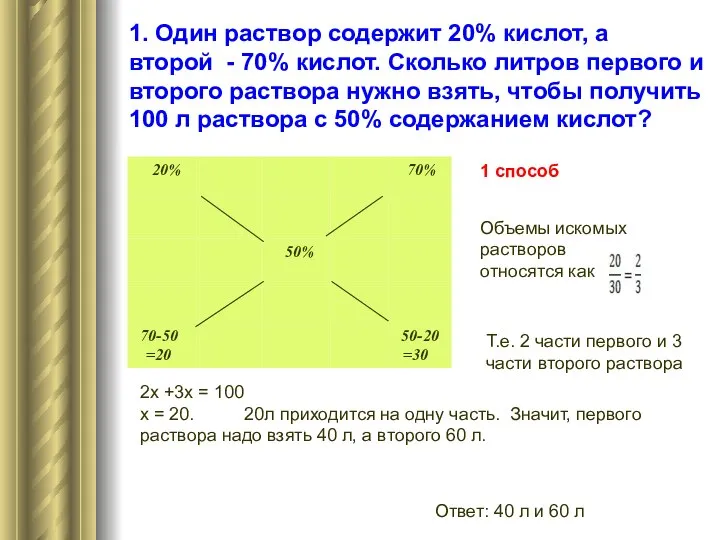
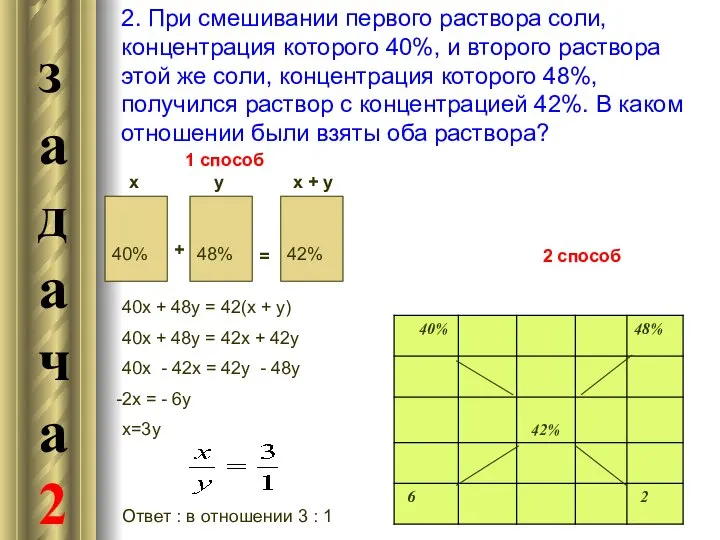
5. Процент содержания меди в первом сплаве на 40% меньше, чем во втором сплаве. После того, как эти слитки сплавили вместе, получили новый сплав с содержанием меди 36%.Определить процентное содержание меди в первоначальных сплавах, если в первом сплаве меди было 6 кг, а во втором 12 кг. 1способ
Пусть х % меди содержалось в первом сплаве, тогда х + 40 % её содержалось во втором. В первом сплаве меди было 6 кг, а во втором 12кг,следовательно,1% первого и второго сплавов имели массы 6:х и 12 :(х + 40)кг соответственно. Поскольку каждый сплав составляет 100%, то их массы будут М1=600:х кг и М2=1200:(х+40) соответственно.
Новый сплав содержит меди то же количество, которое было до сплавления в двух слитках, т.е. 6+12=18 кг. Это по условию задачи составляет 36% нового сплава, поэтому масса нового сплава есть: 18:36*100=50 кг.
Масса нового сплава состоит из масс двух старых сплавов, так
что 50= (600:х)+ 1200:(х+40)
1= (12:х)+ 24:(х+40).
х1=20, х2=-24; х>0,то х=20. 20%+40%=60%
Ответ: 20%, 60%
задача5

5. Процент содержания меди в первом сплаве на 40% меньше, чем во втором сплаве. После того, как эти слитки сплавили вместе, получили новый сплав с содержанием меди 36%.Определить процентное содержание меди в первоначальных сплавах, если в первом сплаве меди было 6 кг, а во втором 12 кг. 2способ
задача5
Х%
Х +40%
36%
+
=
M1=6:х
M2=12:(х+40)
6:х + 12:(х+40)
Меди 6 кг
Меди 12 кг
Меди 18 кг
18:36=0,5 нового сплава
6:х + 12:(х+40) = 0,5
+
= 1
12(х+40)+24х= х(х+40)
12х+480+24х= х2 + 40х
х2 + 4х + 480 = 0
х1=20,
х2=-24 –посторонний корень
Значит, 20% меди в 1 сплаве, 20%+40%=60%

Даны два куска с различным содержанием олова. Первый, массой 300 г. содержит 20% олова. Второй, массой 200 г, содержит 40% олова. Сколько % олова будет содержать сплав, полученный из этих кусков? (28%)
В сосуд, содержащий 5 л 12% водного раствора кислоты, добавили 7л воды. Сколько % составляет концентрация, получившегося раствора? (5%)
САМОСТОЯТЕЛЬНО

Торговец продает орехи двух сортов. Первый по 90 центов, второй по 60 центов за 1 кг. Он хочет получить 50 кг смеси по 72 цента за кг. Сколько потребуется взять орехов каждого сорта? (20 кг, 30 кг)
Сколько фунтов меди надо сплавить с 75 фунтами серебра 72-й пробы, чтобы получить серебро 64-й пробы? (9,375 фунта)
САМОСТОЯТЕЛЬНО

САМОСТОЯТЕЛЬНО
5. Торговец продает вино двух сортов: по 10 и по 6 гривен за ведро. Какие части этих вин ему надо взять, чтобы получить вино ценой в 7 гривен за ведро? (1/4 ведра и ¾ ведра)
6. Сколько томатной пасты, содержащей 30% воды, получится из 28 тонн томатов, содержащих 95% воды?(2 т)

САМОСТОЯТЕЛЬНО
Некий леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза успокоил всех, сказав: «В нашем лесу 99% деревьев – сосны. После вырубки сосна будет составлять 98% всех деревьев.» Какую часть леса вырубит леспромхоз? (50%)

8. Смешав 70%-й и 60% -й растворы кислоты и добавив 2 кг чистой воды, получили 50% раствор кислоты. Если бы вместо 2кг воды добавили 2 кг 90% раствора той же кислоты, то получили бы 70% раствор кислоты. Сколько кг 70% раствора использовали для получения смеси? (3 кг)
9. Первый сплав содержит 5% меди, второй - 13% меди. Масса второго сплава больше массы первого на 2 кг. Сплавив их вместе, получили третий сплав, содержащий 10% меди. Найти массу третьего сплава. (8 кг)
САМОСТОЯТЕЛЬНО

10. Смешали 4л 15% водного раствора некоторого вещества с 6 л 25% водного раствора этого же вещества. Сколько % составляет концентрация получившегося раствора? (21%)
11. Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% раствора этого же вещества. Сколько % составляет концентрация получившегося раствора? (17%)
САМОСТОЯТЕЛЬНО

12. Имеются два сплава. Первый содержит 10% никеля, второй – 30% никеля, из этих двух сплавов получили третий сплав, массой 200 кг, содержащий25% никеля. На сколько килограммов масса первого сплава меньше массы второго сплава? (на 100 кг)
13. Первый сплав содержит 10 % меди, второй сплав – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найти массу третьего сплава. (9кг)
САМОСТОЯТЕЛЬНО

Смешав 30% и 60% растворы кислоты и добавив 10кг чистой воды, получили 36% раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50% раствора этой же кислоты, то получили бы 41% раствор кислоты. Сколько килограммов 30% раствора использовали для получения смеси? (60 кг)
При смешивании первого раствора кислоты 20% концентрации со вторым - 50% концентрации, получили 30% раствор кислоты. В каком отношении были взяты первый и второй растворы?(2 : 1)
САМОСТОЯТЕЛЬНО