- Главная
- Математика
- Статистический анализ результатов мониторинга

Содержание
- 2. Каждому физическому измерению присуща некоторая погрешность, которая в лучшем случае может быть снижена лишь до какого-то
- 3. Далее мы обсуждаем типы ошибок, возникающих при проведении анализа, методы их выявления, а также способы оценки
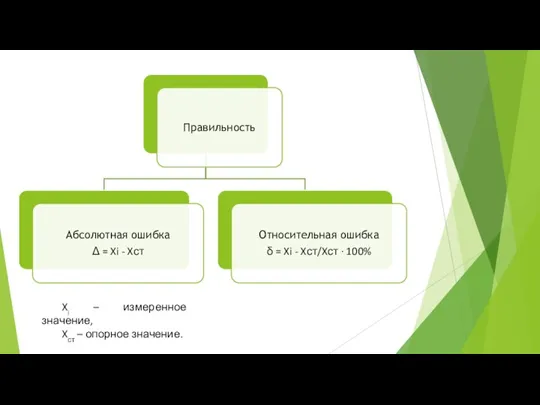
- 4. Xi – измеренное значение, Xст – опорное значение.
- 5. Нужно понимать, что хорошая сходимость не означает, что высока правильность. Например, на рисунке представлены результаты определения
- 6. Обратите внимание на то, что аналитик 1 получил относительно высокую воспроизводимость и высокую правильность. Аналитик 2,
- 7. Классификация ошибок
- 8. Типы систематических ошибок Индивидуальные – ошибки, возникающие в результате незнания, небрежности, предвзятости или физических недостатков. Инструментальные
- 9. Статистическая обработка полученных результатов При обсуждении общих принципов количественного анализа уже были затронуты вопросы воспроизводимости и
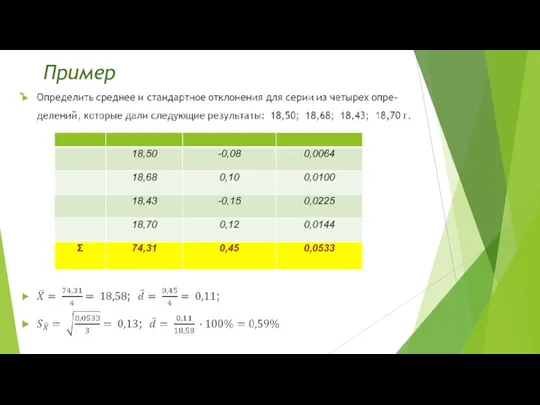
- 12. Пример
- 15. Пример
- 17. Пример Определите, какие ошибки из перечисленных являются случайными: 1) ошибка при однократном измерении сопротивления проводника; 2)
- 18. Случайная ошибка, возникающая при измерении некоторой величины, может теоретически принимать любые значения. Она является непрерывной случайной
- 19. Уильям Силей Госсет Уильям Силей Госсет родился 13 июня 1876 г. в Английском городе Кантербури, Англия,
- 21. Скачать презентацию
Слайд 2Каждому физическому измерению присуща некоторая погрешность, которая в лучшем случае может быть
Каждому физическому измерению присуща некоторая погрешность, которая в лучшем случае может быть

Достоверность аналитических измерений прямо зависит от времени и усилий, затраченных на их получение. Чтобы добиться десятикратного увеличения точности может понадобиться дополнительная работа в течение многих часов, дней или даже недель. Поэтому опытный исследователь в первую очередь устанавливает желаемую степень достоверности результата, так как это определит затраты времени и труда на выполнение анализа. Тщательное продумывание исследования в самом начале часто обеспечивает большую экономию времени и труда. Не следует тратить много времени в погоне за высокой точностью там, где она не нужна.
Слайд 3Далее мы обсуждаем типы ошибок, возникающих при проведении анализа, методы их выявления,
Далее мы обсуждаем типы ошибок, возникающих при проведении анализа, методы их выявления,

Обычно исследователь повторяет анализ от 2 до 5 раз. Два раза – минимум, т.к. необходимо, чтобы результаты были достоверными.
Чем больше выборка, тем достовернее результаты, но по двум значениям можно сделать выводы.
Некоторые определения
Сходимость – близость результатов, выполненных одним аналитиком (исследователем) за короткий период времени.
Воспроизводимость – близость результатов, выполненных разными исследователями или за более длительный промежуток времени.
Согласно ГОСТ Р ИСО 5725-1-2002
Прецизионность – степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях.
Показатели прецизионности: сходимость, воспроизводимость.
Сходимость – прецизионность в условиях повторяемости.
Воспроизводимость – прецизионность в условиях воспроизводимости.
Правильность – степень близости полученного значения к значению, принятому за действительное, и выражается ошибкой (погрешностью).
Слайд 4Xi – измеренное значение,
Xст – опорное значение.
Xст – опорное значение.
Слайд 5Нужно понимать, что хорошая сходимость не означает, что высока правильность.
Например, на
Нужно понимать, что хорошая сходимость не означает, что высока правильность.
Например, на
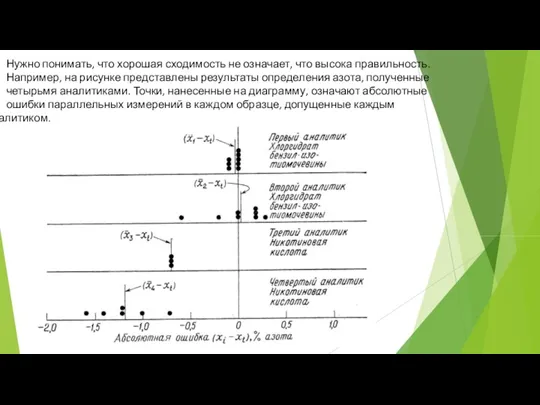
четырьмя аналитиками. Точки, нанесенные на диаграмму, означают абсолютные
ошибки параллельных измерений в каждом образце, допущенные каждым аналитиком.
Слайд 6Обратите внимание на то, что аналитик 1 получил относительно высокую воспроизводимость и
Обратите внимание на то, что аналитик 1 получил относительно высокую воспроизводимость и

Наблюдаемую на рисунке картину можно объяснить, предположив, что при проведении эксперимента допущены ошибки двух основных типов, причем ошибки одного типа не связаны с воспроизводимостью измерений.
Слайд 7Классификация ошибок
Классификация ошибок

Слайд 8Типы систематических ошибок
Индивидуальные – ошибки, возникающие в результате незнания, небрежности, предвзятости или
Типы систематических ошибок
Индивидуальные – ошибки, возникающие в результате незнания, небрежности, предвзятости или

Инструментальные – ошибки приборов (измерительного оборудования).
Ошибки метода анализа.
Постоянная – величина постоянной ошибки не зависит от измеряемого количества.
Изменяющаяся – линейно изменяющаяся ошибка, наоборот, уменьшается или возрастает по абсолютной величине пропорционально размеру пробы, взятой для анализа.
Слайд 9Статистическая обработка полученных результатов
При обсуждении общих принципов количественного анализа уже были затронуты
Статистическая обработка полученных результатов
При обсуждении общих принципов количественного анализа уже были затронуты

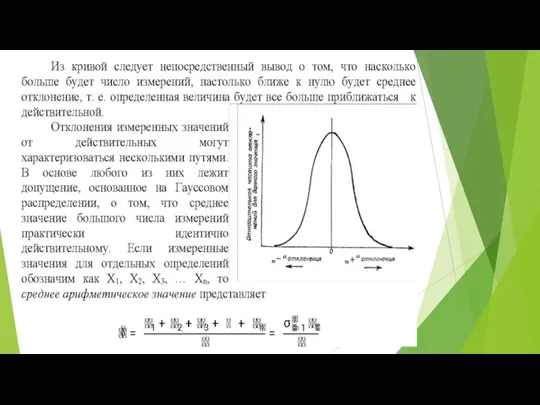
Случайные ошибки обладают нормальным распределением, которое графически изображается так называемой Гауссовой кривой, представленной на рисунке. Эта кривая отражает две основные зависимости, которым подчиняются случайные ошибки:
а) малые отклонения от действительного значения более часты, чем большие;
б) частота, с которой встречаются положительные и отрицательные ошибки, одинакова.
Слайд 12Пример
Пример
Слайд 15Пример
Пример

Слайд 17Пример
Определите, какие ошибки из перечисленных являются случайными:
1) ошибка при однократном измерении сопротивления
Пример
Определите, какие ошибки из перечисленных являются случайными: 1) ошибка при однократном измерении сопротивления

Решение
В случае 2) ошибка является суммой систематической и случайной ошибок, потому что отклонение каждый раз происходит в одну и ту же сторону. Если бы отклонение каждый раз происходило ещё и на одну и ту же величину, то ошибка была бы чисто систематической. В случае 4) отклонение зафиксировано в разные стороны – это признак того, что систематическая ошибка, если и есть, то меньше случайной. Про ошибки в 1) и 3) определённо ничего сказать нельзя, так как сделано всего одно измерение.
Слайд 18Случайная ошибка, возникающая при измерении некоторой величины, может теоретически принимать любые значения.
Случайная ошибка, возникающая при измерении некоторой величины, может теоретически принимать любые значения.
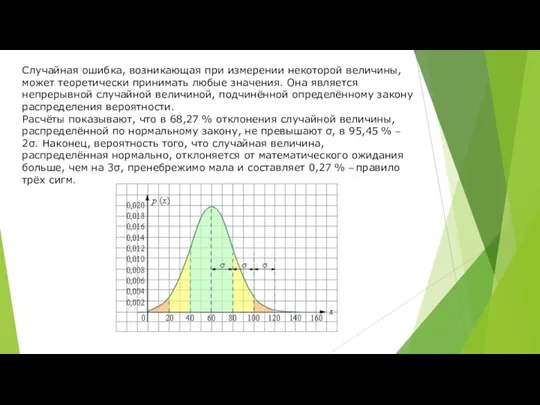
Расчёты показывают, что в 68,27 % отклонения случайной величины, распределённой по нормальному закону, не превышают σ, в 95,45 % – 2σ. Наконец, вероятность того, что случайная величина, распределённая нормально, отклоняется от математического ожидания больше, чем на 3σ, пренебрежимо мала и составляет 0,27 % – правило трёх сигм.
Слайд 19Уильям Силей Госсет
Уильям Силей Госсет родился 13 июня 1876 г. в Английском городе Кантербури,
Уильям Силей Госсет
Уильям Силей Госсет родился 13 июня 1876 г. в Английском городе Кантербури,

Он пошел в школу в Уинчестере и был хорошо образован перед поступлением в Новый Колледж в Оксфорде. Здесь он завоевал первую степень по химии в 1899 году. После получения своей степени химика он получил работу в пивоваренном заводе Гуиннеса в Дублине в 1899, где он выполнял важную статистическую работу, но на которую никогда не нанимали статиста. Именно окружающая среда в Гуиннессе сделала его статистом. Пивоваренный завод был заинтересован в том, чтобы они могли делать лучшее пиво.
В 1900 году была открыта Научно-исследовательская лаборатория Гуиннесса, которую возглавил наиболее выдающийся молодой химик Хорас Броун. Хорас Броун наряду с другими варевами задавался вопросом, как получить сырье для назревающего пива наиболее дешево, но получить при этом максимум. Было много факторов, которые они были должны принять во внимание типа множества видов ячменя и хмеля, какие условия изготовления, факторы культивирования и назревания. После нескольких лет исследования, учитывая что им давали свободу в исследовании условий назревания. Это дало Госсету шанс, чтобы работать как статистик. Он был способен брать данные от различных примеров назревания, что помогало ему выяснить, который путь был лучшее. Поскольку молодые пивовары работают вместе, это казалось естественным для них, чтобы собирать данные для Госсета, чтобы решить числовые проблемы.



 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа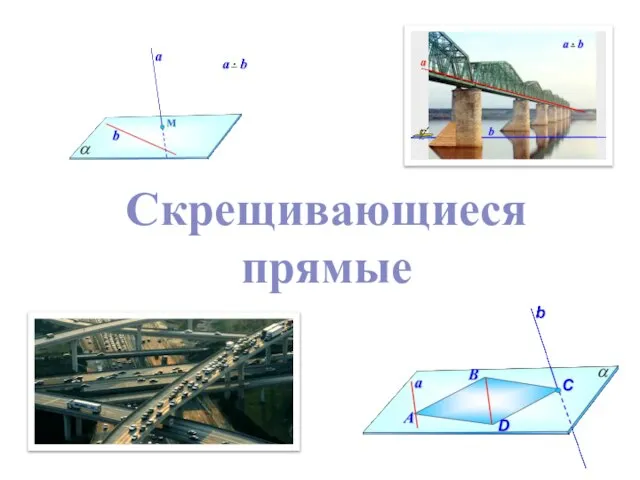 Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15