Основы теории графов

ОПРЕДЕЛЕНИЯ
Графом G называется любая пара (V,U), где V = {v1, v2, ... } - множество элементов любой природы, а U = {u1, u2, ... } – семейство пар элементов из V, причем допускаются пары вида (vi, vi) и одинаковые пары.
Если пары в U рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным (орграфом).
Элементы множества V называются вершинами графа, а пары из U в неориентированном графе называются ребрами, а в орграфе – ориентированными ребрами или чаще дугами.
Ребро u = (vi, vj) в неориентированном графе соединяет вершины vi и vj, а в ориентированном графе дуга u = (vi, vj) идет из вершины vi в вершину vj.

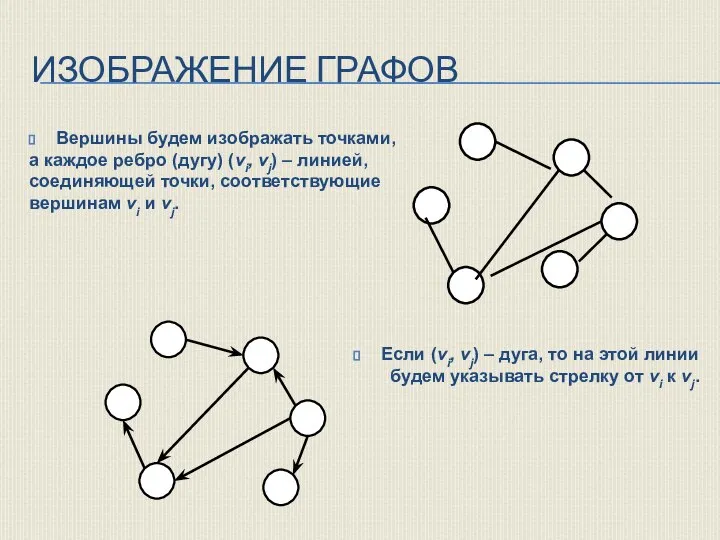
ИЗОБРАЖЕНИЕ ГРАФОВ
Вершины будем изображать точками,
а каждое ребро (дугу) (vi, vj) – линией,
соединяющей точки, соответствующие
вершинам vi и vj.
Если (vi, vj) – дуга, то на этой линии
будем указывать стрелку от vi к vj.

ОПРЕДЕЛЕНИЯ
Вершины vi и vj смежны в графе G = (V, U), если в U входит пара (vi, vj) или (vj, vi). Ребро (дуга) (vi, vj) инцидентно вершинам vi и vj.
Два различных ребра графа называются смежными, если они имеют, по крайней мере, одну общую вершину.
Пара вида (vi, vi) называется петлей в вершине vi.
Если пара (vi, vj) встречается в U более одного раза, то говорят, что (vi, vj) – кратное ребро.

ОПРЕДЕЛЕНИЯ
Каждое ребро u из U (кроме петель) инцидентно ровно двум вершинам vi, vj, которые оно соединяет.
Степенью St(v) вершины v неориентированного графа G называется число ребер, инцидентных v.
Вершина степени 0 называется изолированной вершиной.
Вершина степени 1 называется висячей или концевой вершиной.
Пусть G=(V,U) – n-вершинный граф, а s1,s2,...,sn – степени его вершин, выписанные в порядке невозрастания: s1 ≥ s2 ≥...≥ sn.
Упорядоченную систему (s1,s2,...,sn) будем называть вектором степеней графа G и кратко обозначать s(G).

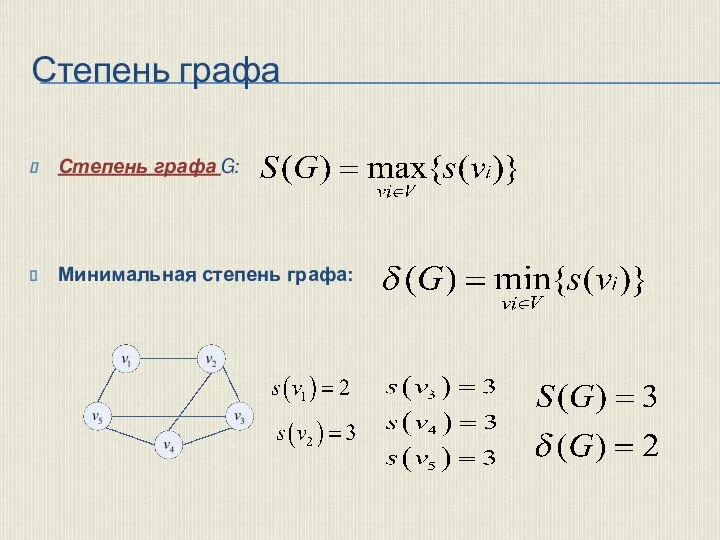
Степень графа G:
Минимальная степень графа:
Степень графа

Cумма степеней вершин
Теорема
Сумма степеней вершин графа есть число четное:
Следствие
Число вершин с нечетными степенями – четно.

Частичные графы и подграфы
Пусть G=(V,U) - некоторый граф
Граф G1=(V1,U1) называется частичным графом графа G, если V1=V и U1⊆ U
Граф G2=(V2,U2) называется подграфом графа G, если:
V2 ⊆V
из vi∈ V2, vj∈ V2, vi и vj смежны в G, следует, что
vi и vj смежны в G2
Граф G3=(V3,U3) называется частичным подграфом графа G, если он является частичным графом подграфа графа G

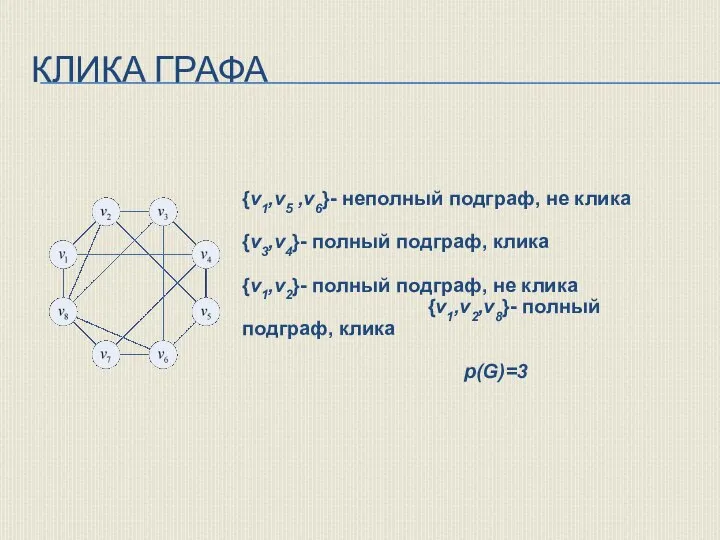
КЛИКА ГРАФА
Пусть G=(V,U) - некоторый граф.
Подграф графа, любые две вершины которого смежны, называется полным подграфом.
Клика графа – любой максимальный по включению полный подграф.
Кликовое число графа ρ(G) (густота или плотность) – максимальное число вершин в кликах данного графа.
Тогда, образно говоря, чем более плотен граф, тем будет больше кликовое число.

КЛИКА ГРАФА
{v1,v5 ,v6}- неполный подграф, не клика
{v3,v4}- полный подграф, клика
{v1,v2}- полный подграф, не клика
{v1,v2,v8}- полный подграф, клика
p(G)=3

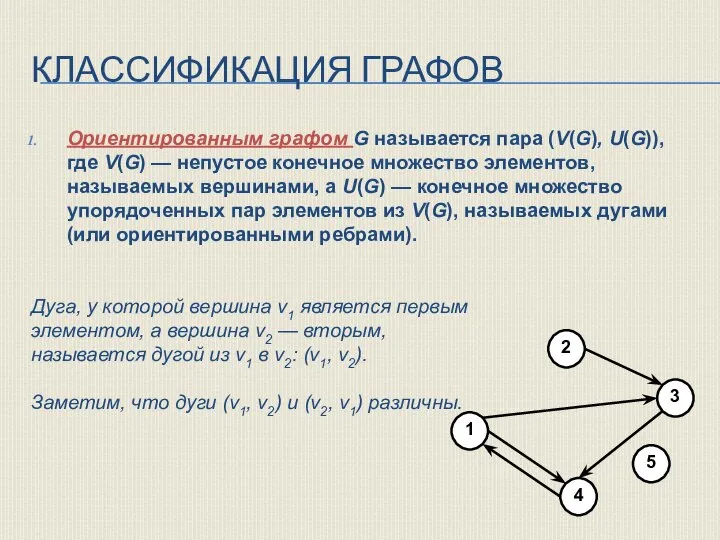
Ориентированным графом G называется пара (V(G), U(G)), где V(G) — непустое конечное множество элементов, называемых вершинами, а U(G) — конечное множество упорядоченных пар элементов из V(G), называемых дугами (или ориентированными ребрами).
Дуга, у которой вершина v1 является первым
элементом, а вершина v2 — вторым,
называется дугой из v1 в v2: (v1, v2).
Заметим, что дуги (v1, v2) и (v2, v1) различны.
КЛАССИФИКАЦИЯ ГРАФОВ

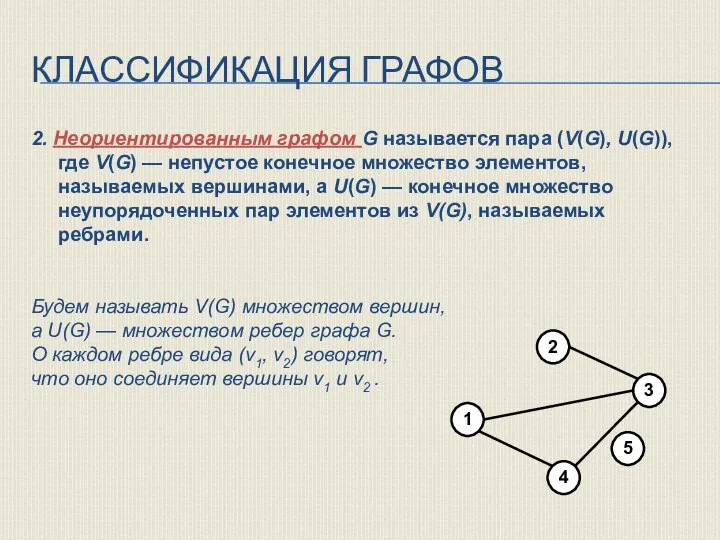
КЛАССИФИКАЦИЯ ГРАФОВ
2. Неориентированным графом G называется пара (V(G), U(G)), где V(G) — непустое конечное множество элементов, называемых вершинами, а U(G) — конечное множество неупорядоченных пар элементов из V(G), называемых ребрами.
Будем называть V(G) множеством вершин,
а U(G) — множеством ребер графа G.
О каждом ребре вида (v1, v2) говорят,
что оно соединяет вершины v1 и v2 .

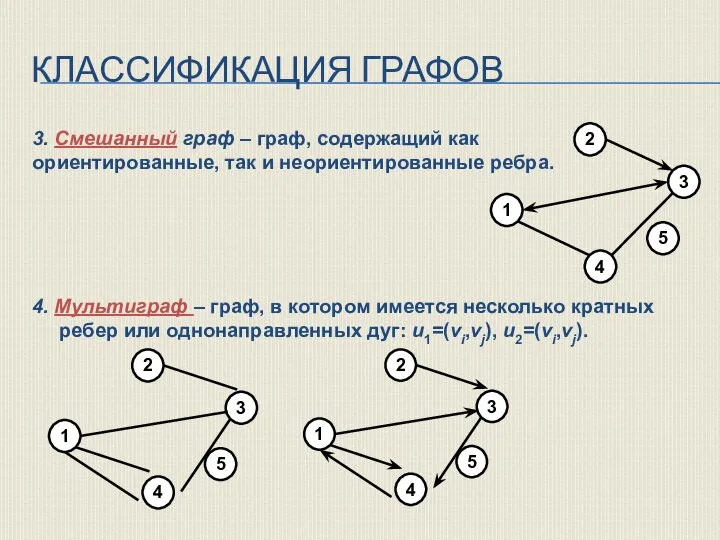
КЛАССИФИКАЦИЯ ГРАФОВ
3. Смешанный граф – граф, содержащий как
ориентированные, так и неориентированные ребра.
4. Мультиграф – граф, в котором имеется несколько кратных ребер или однонаправленных дуг: u1=(vi,vj), u2=(vi,vj).

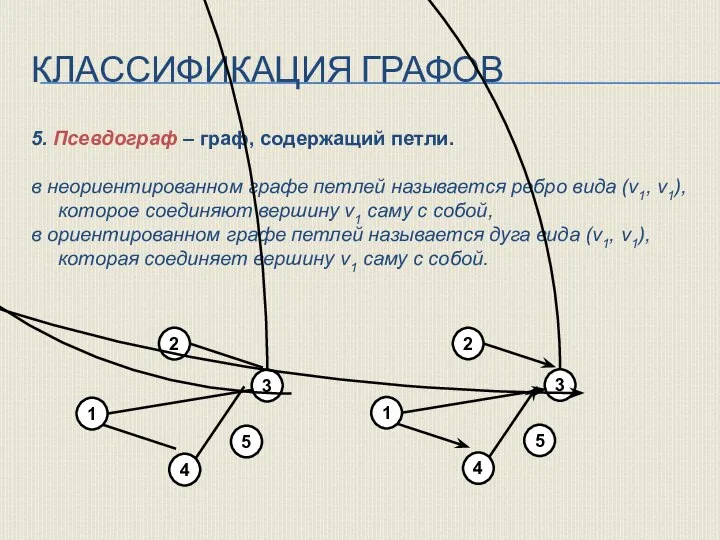
КЛАССИФИКАЦИЯ ГРАФОВ
5. Псевдограф – граф, содержащий петли.
в неориентированном графе петлей называется ребро вида (v1, v1), которое соединяют вершину v1 саму с собой,
в ориентированном графе петлей называется дуга вида (v1, v1), которая соединяет вершину v1 саму с собой.

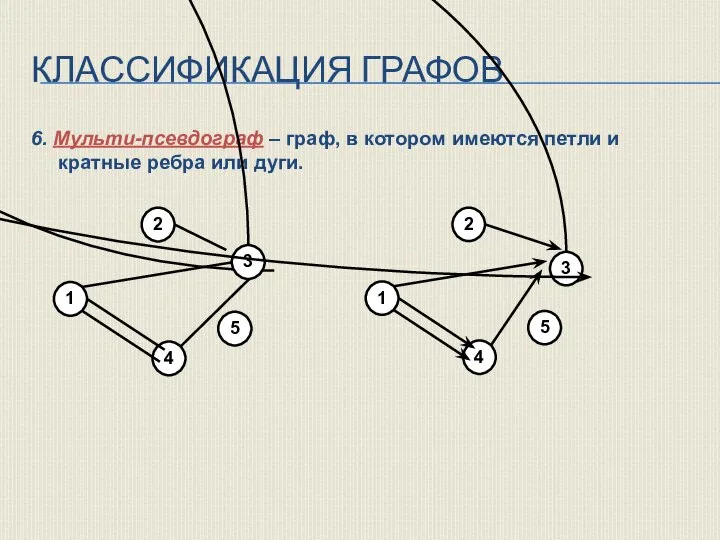
КЛАССИФИКАЦИЯ ГРАФОВ
6. Мульти-псевдограф – граф, в котором имеются петли и кратные ребра или дуги.

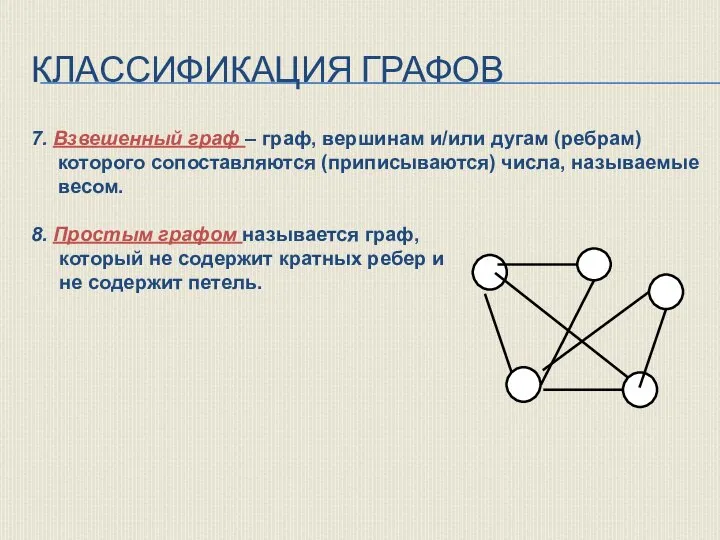
КЛАССИФИКАЦИЯ ГРАФОВ
7. Взвешенный граф – граф, вершинам и/или дугам (ребрам) которого сопоставляются (приписываются) числа, называемые весом.
8. Простым графом называется граф,
который не содержит кратных ребер и
не содержит петель.

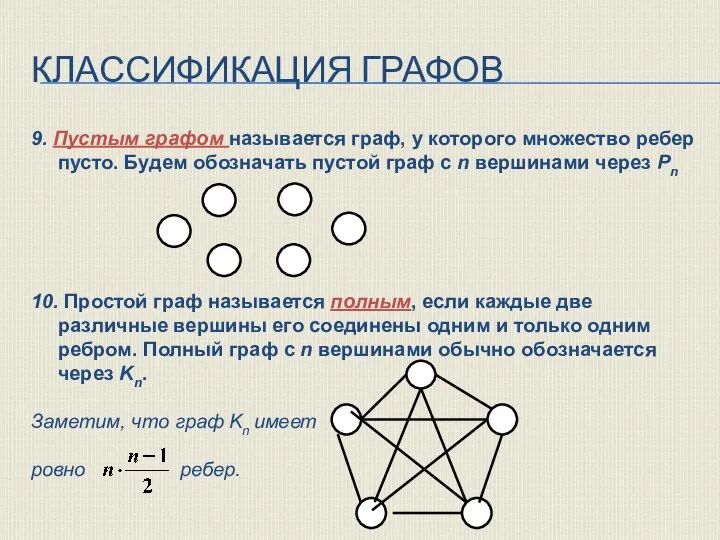
КЛАССИФИКАЦИЯ ГРАФОВ
9. Пустым графом называется граф, у которого множество ребер пусто. Будем обозначать пустой граф с n вершинами через Pn
10. Простой граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром. Полный граф с n вершинами обычно обозначается через Kn.
Заметим, что граф Kn имеет
ровно ребер.

КЛАССИФИКАЦИЯ ГРАФОВ
11. Граф, у которого все n вершин имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна r, то граф называется регулярным степени r .
Заметим, что регулярный граф степени r на n вершинах имеет ровно ребер.
12. Двудольный граф — это граф G(V,U), такой, что множество вершин V разбито на два непересекающихся подмножества V1 и V2, причeм всякое ребро U инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2). Множества V1 и V2 называются «долями» двудольного графа.

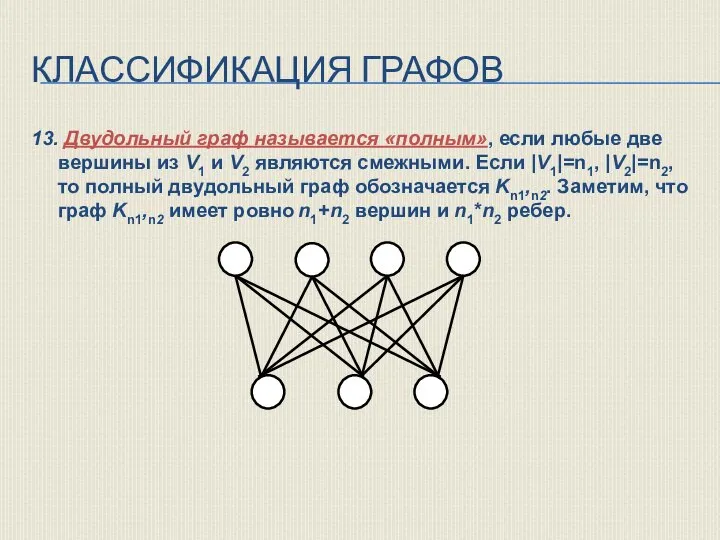
КЛАССИФИКАЦИЯ ГРАФОВ
13. Двудольный граф называется «полным», если любые две вершины из V1 и V2 являются смежными. Если |V1|=n1, |V2|=n2, то полный двудольный граф обозначается Kn1,n2. Заметим, что граф Kn1,n2 имеет ровно n1+n2 вершин и n1*n2 ребер.

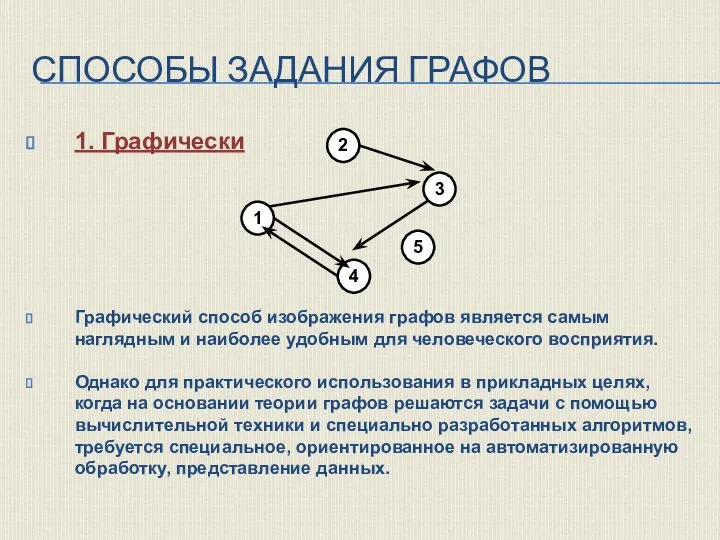
СПОСОБЫ ЗАДАНИЯ ГРАФОВ
1. Графически
Графический способ изображения графов является самым наглядным и наиболее удобным для человеческого восприятия.
Однако для практического использования в прикладных целях, когда на основании теории графов решаются задачи с помощью вычислительной техники и специально разработанных алгоритмов, требуется специальное, ориентированное на автоматизированную обработку, представление данных.

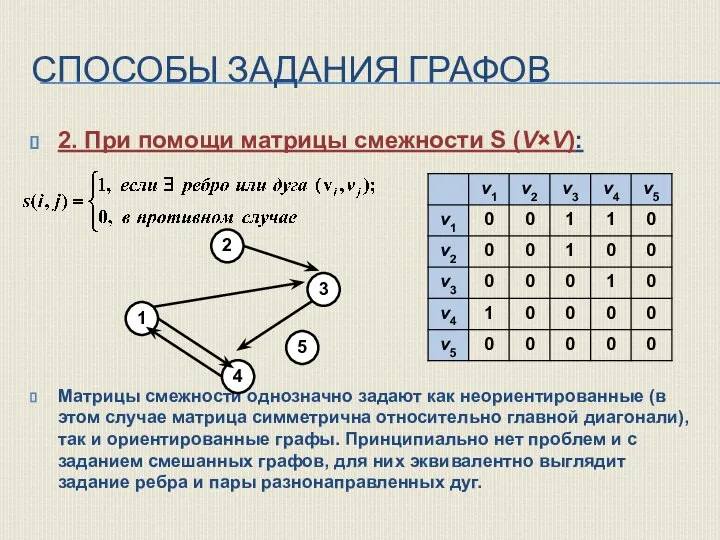
СПОСОБЫ ЗАДАНИЯ ГРАФОВ
2. При помощи матрицы смежности S (V×V):
Матрицы смежности однозначно задают как неориентированные (в этом случае матрица симметрична относительно главной диагонали), так и ориентированные графы. Принципиально нет проблем и с заданием смешанных графов, для них эквивалентно выглядит задание ребра и пары разнонаправленных дуг.

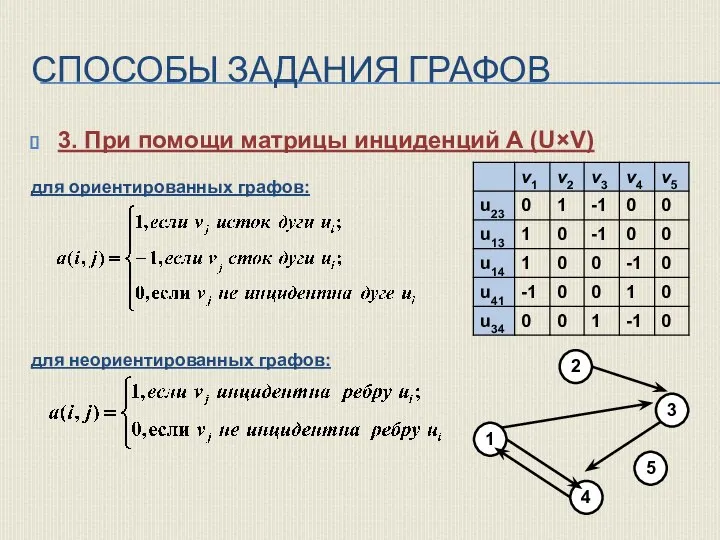
СПОСОБЫ ЗАДАНИЯ ГРАФОВ
3. При помощи матрицы инциденций А (U×V)
для ориентированных графов:
для неориентированных графов:

СПОСОБЫ ЗАДАНИЯ ГРАФОВ
Матрицы инциденций однозначно задают как неориентированные, так и ориентированные графы.
В принципе нет никаких препятствий для задания смешанных графов – в отличие от матрицы смежности в этом случае задание ребра и пары разнонаправленных дуг будет отличаться.
Никаких проблем не возникает с мультиграфами (и в ориентированном, и в неориентированном случаях), а также с неориентированными псевдографами.

СПОСОБЫ ЗАДАНИЯ ГРАФОВ
Неоднозначность возникает при задании ориентированных псевдографов: на пересечении строки, помеченной петлей, и столбца, помеченного вершиной, на которой эта петли присутствует, по правилу должны одновременно находиться как 1 так и –1.
Из этой ситуации имеется выход: вместо одной матрицы А (U×V) граф задается двумя матрицами – истоков А+ (U×V) и стоков А- (U×V):

СПОСОБЫ ЗАДАНИЯ ГРАФОВ
4. При помощи функционального представления
Г1 и Г-1
Г1(vi) = {vj}: ∃ дуга (vi , vj);
Г-1(vi) = {vj}: ∃ дуга (vj, vi ).
При помощи функционального представления однозначно задаются как неориентированные (в этом случае Г1 = Г-1), так и ориентированные и смешанные графы. Как и в случае с матрицей смежности, для смешанных графов эквивалентно выглядит задание ребра и пары разнонаправленных дуг.
Г1(v1)={v3,v4}; Г-1(v1)={v4};
Г1(v2)={v3}; Г-1(v2)=∅;
Г1(v3)={v4}; Г-1(v3)={v1,v2,};
Г1(v4)={v1}; Г-1(v4)={v1,v3};
Г1(v5)=∅; Г-1(v5)=∅.

ИЗОМОРФИЗМ ГРАФОВ
Изоморфизмом графов G1 и G2 называется биекция между множествами вершин графов такая, что любые две вершины графа G1 смежны тогда и только тогда, когда соответствующие им вершины смежны в графе G2 .
Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер.
В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов.
Если изоморфизм графов установлен, они называются изоморфными.

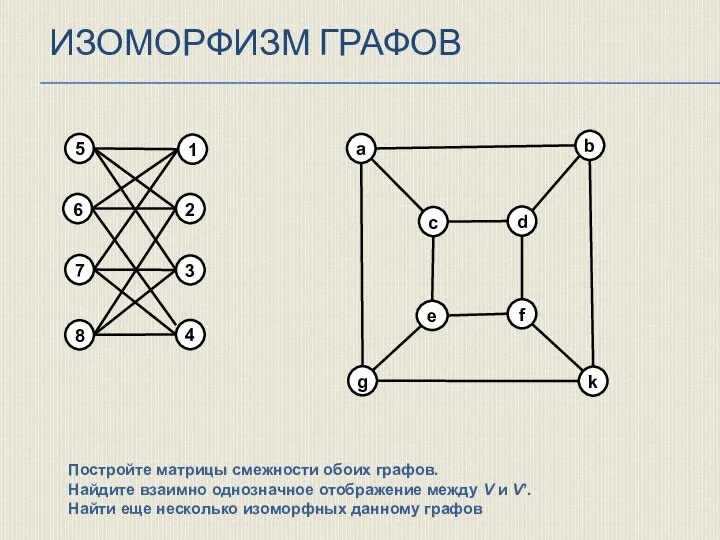
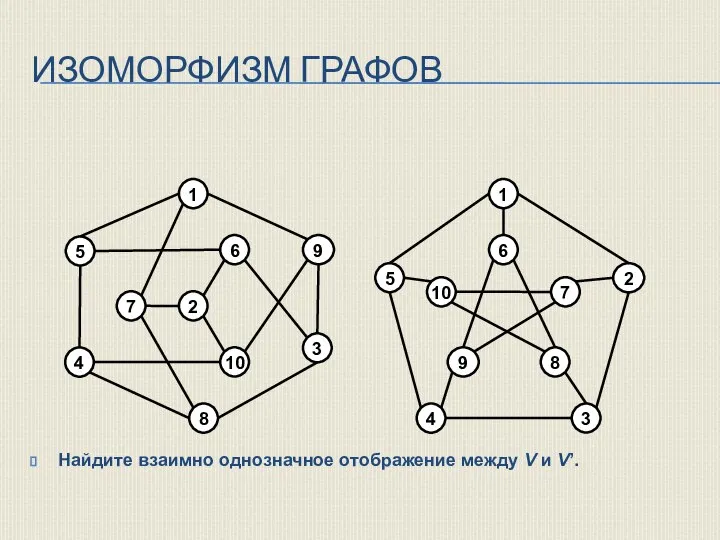
ИЗОМОРФИЗМ ГРАФОВ
Взаимно однозначное отображение множества вершин графа G1 на множество вершин графа G2, сохраняющее смежность, называют изоморфизмом.
Изоморфные графы – это графы, которые имеют одинаковое число вершин и одинаковое число ребер, причем для вершин графов можно ввести одинаковые обозначения таким образом, что неупорядоченные пары вершин, обозначающие ребра, у изоморфных графов будут одинаковы.
Иными словами, графы называются изоморфными, если существует такая нумерация вершин в этих графах, что они имеют одну и ту же матрицу смежности (фактически изоморфные графы – это одинаковые графы, которые отличаются только другим изображением).

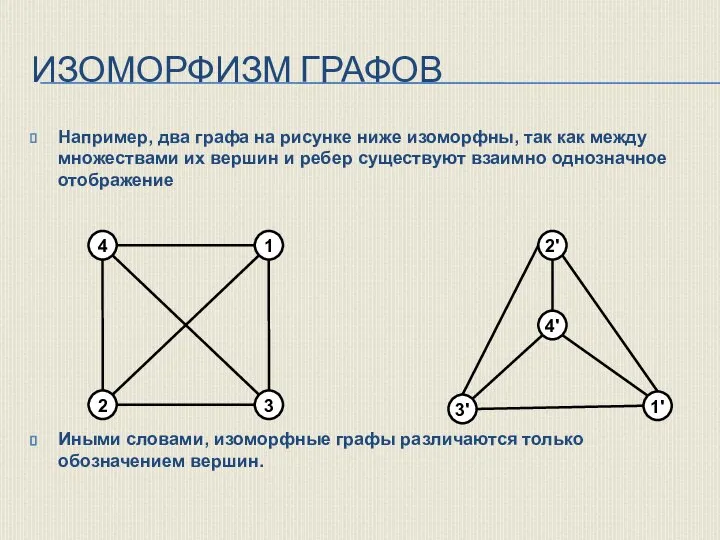
ИЗОМОРФИЗМ ГРАФОВ
Например, два графа на рисунке ниже изоморфны, так как между множествами их вершин и ребер существуют взаимно однозначное отображение
Иными словами, изоморфные графы различаются только обозначением вершин.
4
3
2
1
1'
3'
4'
2'

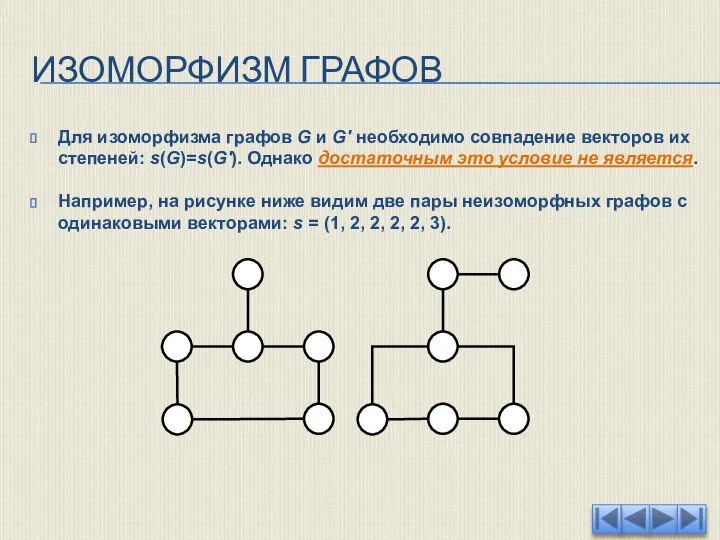
ИЗОМОРФИЗМ ГРАФОВ
Для изоморфизма графов G и G' необходимо совпадение векторов их степеней: s(G)=s(G'). Однако достаточным это условие не является.
Например, на рисунке ниже видим две пары неизоморфных графов с одинаковыми векторами: s = (1, 2, 2, 2, 2, 3).

ИЗОМОРФИЗМ ГРАФОВ
1
3
5
8
4
6
7
2
b
k
а
f
e
c
g
d
Постройте матрицы смежности обоих графов.
Найдите взаимно однозначное отображение между V и V’.
Найти еще несколько изоморфных данному графов

ИЗОМОРФИЗМ ГРАФОВ
Найдите взаимно однозначное отображение между V и V’.

Количественная или качественная характеристики, неизменные для всех изоморфных между собой графов (орграфов) называется ИНВАРИАНТОМ
Примеры инвариантов графа G : количество вершин n(G), количество ребер m(G) и вектор степеней s(G)=(s1,s2,...,sn), который в частности, дает числовые инварианты минимальной и максимальной степени вершин графа:
min_st(vi) и max_st(vi), i=1,2,...,n.
Поиск полной системы инвариантов графа, задающей граф с точность до изоморфизма – основная задача теории графов
(полная система инвариантов ещё не найдена)
ИНВАРИАНТЫ ГРАФА

ЗАДАЧА 2.1.
Дан неориентированный граф, заданный своим функциональным представлением:
Г(v1) = {v1, v2, v3, v4, v5};
Г(v2) = {v1, v3};
Г(v3) = {v1, v2, v3, v5};
Г(v4) = {v1, v5};
Г(v5) = {v1, v3, v4};
Г(v6) = ∅.
Задать этот граф тремя другими способами: графически; с помощью матрицы инциденций; с помощью матрицы смежности.

ЗАДАЧА 2.1.
Решение:
Подобные задачи на построение графа необходимо начинать с определения всех вершин, входящих в множество V. Для функционального представления множество вершин графа совпадает с областью определения функции Г. В нашем случае получаем, что V={v1,v2,v3,v4,v5,v6}. Также необходимо заметить, что множество V может и не совпадать с объединением множеств Г(vi). Что очень хорошо видно в этом примере: вершина v6 не входит ни в одно из множеств, порождаемых функцией Г.
а) Построение графического способа задания графа.
Графический способ изображения графов является самым наглядным и наиболее удобным для человеческого восприятия, потому и решение любой задачи в теории графов лучше всего начинать с построения графического представления.

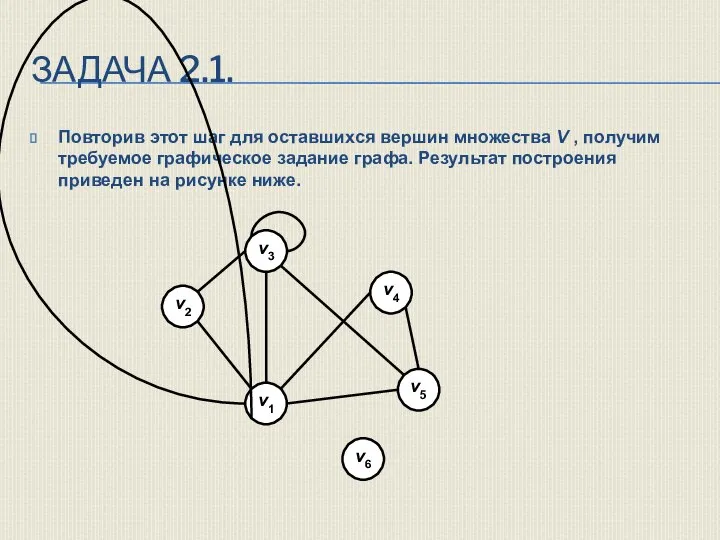
ЗАДАЧА 2.1.
Сначала изобразим в виде кружков с написанным названием внутри все вершины, входящие в множество V.
Они могут находится совершенно в произвольных местах и не обязаны каким-либо образом быть упорядочены.
Выберем вершину v1 и с помощью линий соединим ее со всеми вершинами, входящими в множество Г(v1), то есть с вершинами v1,v2,v3,v4,v5.
Сама же вершина v1 соединяется сама с собой с помощью петли.
Далее рассмотрим вершину v2, она смежна с вершинам v1 и v3, но ребро (v1,v2) уже построено, а в случае неориентированного графа, значит, и ребро (v2,v1) тоже построено.
Таким образом необходимо построить ребро только между вершиами v2 и v3.

ЗАДАЧА 2.1.
Повторив этот шаг для оставшихся вершин множества V , получим требуемое графическое задание графа. Результат построения приведен на рисунке ниже.

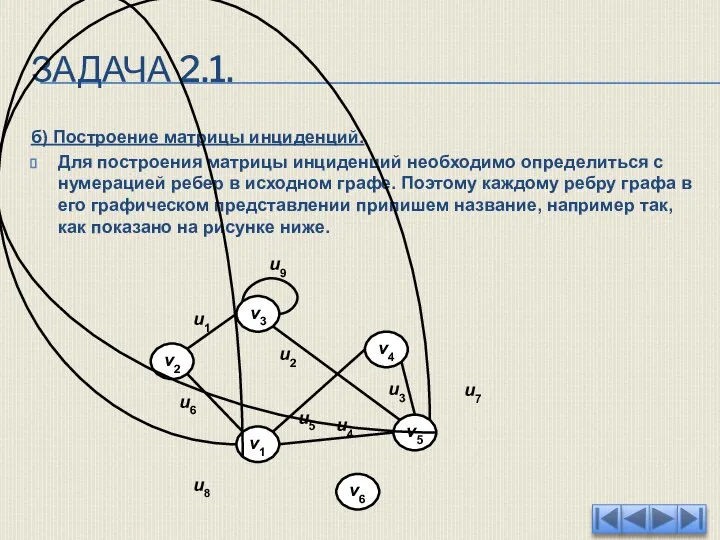
ЗАДАЧА 2.1.
б) Построение матрицы инциденций.
Для построения матрицы инциденций необходимо определиться с нумерацией ребер в исходном графе. Поэтому каждому ребру графа в его графическом представлении припишем название, например так, как показано на рисунке ниже.

ЗАДАЧА 2.1.
Далее необходимо построить матрицу размерности девять на шесть, перечислив ребра ui в первом столбце, а вершины vj – в первой строке.
Рассмотрим заполнение строки, соответствующей ребру u1.
Как видно из рисунка ребро u1 инцидентно вершинам v2 и v3, а значит в соответствующих им ячейках строки u1 ставим единицы.
Повторяем тот же алгоритм для ребер u2, u3, u4, u5 и u6.
В случае же ребер u7, u8 и u9 единица оказывается только в ячейке, соответствующей вершине, с которой данное ребро непосредственно соединено (т.о. для петель в строке матрицы инциденций стоит одна единичка).
Получившаяся в результате матрица инциденций представлена на рисунке ниже.

ЗАДАЧА 2.1.
Получившаяся в результате матрица инциденций:

ЗАДАЧА 2.1.
в) Построение матрицы смежности.
Построение матрицы смежности легче производить по графическому заданию графа.
Для этого сначала необходимо построить матрицу размерности шесть на шесть, по вертикали и горизонтали перечислив вершины vi.
Рассмотрим построение строки, соответствующей вершине vi: данная вершина смежна вершинам v2, v3, v4, и v5, а значит в соответствующих им ячейках матрицы проставляем единицы.
То же повторяем для вершин v2, v3, v4 и v5.
Вершина v6 не связана ребром ни с одной другой вершиной графа, а потому матрица смежности содержит соответствующую ей нулевую строку и нулевой столбец.

ЗАДАЧА 2.1.
Полученная матрица смежности представлена на рисунке ниже.
Как и следовало ожидать, матрица смежности для неориентированного графа оказалась симметричной.

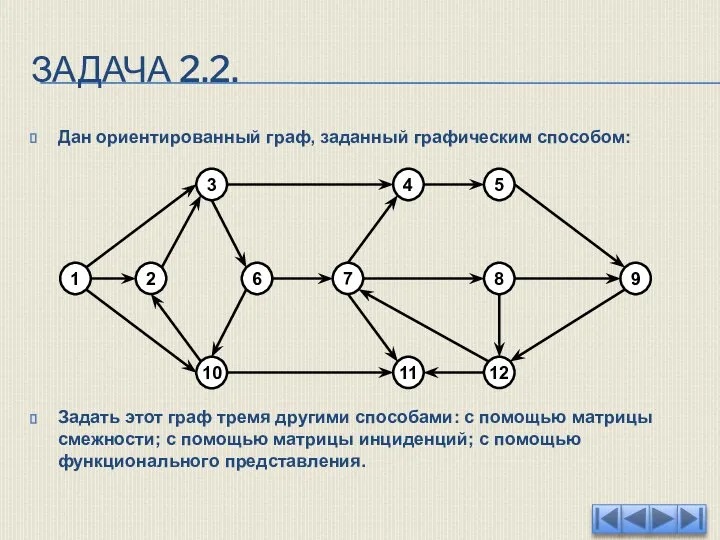
ЗАДАЧА 2.2.
Дан ориентированный граф, заданный графическим способом:
Задать этот граф тремя другими способами: с помощью матрицы смежности; с помощью матрицы инциденций; с помощью функционального представления.

ЗАДАЧА 2.2.
Как видно из графического представления граф содержит 12 вершин. Теперь можно начинать построение требуемых способов задания графа.
а) Построение матрицы смежности.
Сначала необходимо отметить принципиальное отличие между матрицей смежности ориентированного и неориентированного графа.
В случае ориентированного графа матрица S не обязательна должна быть симметричной. Например, как видно из графического представления графа, дуга (v1,v2) принадлежит множеству U, а дуга (v2,v1) – нет.
Сначала, как и в прошлом задании, построим матрицу размерности 12 на 12, по вертикали и горизонтали перечислив вершины vi. Рассмотрим вершину v1. Как видно из графического представления графа, из v1 исходят дуги, приходящие в вершины v2, v3, v10, поэтому, в соответствующих им ячейках строки v1 ставим единицы. Далее рассмотрим вершину v2: по той же схеме получаем
единицу в столбце v3.

ЗАДАЧА 2.2.
Продолжая этот алгоритм для всех оставшихся вершин, получим матрицу смежности, представленную на рисунке ниже.

ЗАДАЧА 2.2.
б) Построение матрицы инциденций.
Как и в случае с матрицей смежности, матрица инциденций неориентированного графа кардинально отличается от матрицы смежности ориентированного графа. Основное отличие заключается в том, что в ней указывается не просто инцидентность ребра ui вершине vj, а так же сведения о том, является ли вершина vj истоком или стоком ребра ui.
Сначала необходимо пронумеровать все дуги исходного графа. Стоит так же заметить, что вершинам v7 и v11 инцидентны одновременно две разнонаправленные дуги.

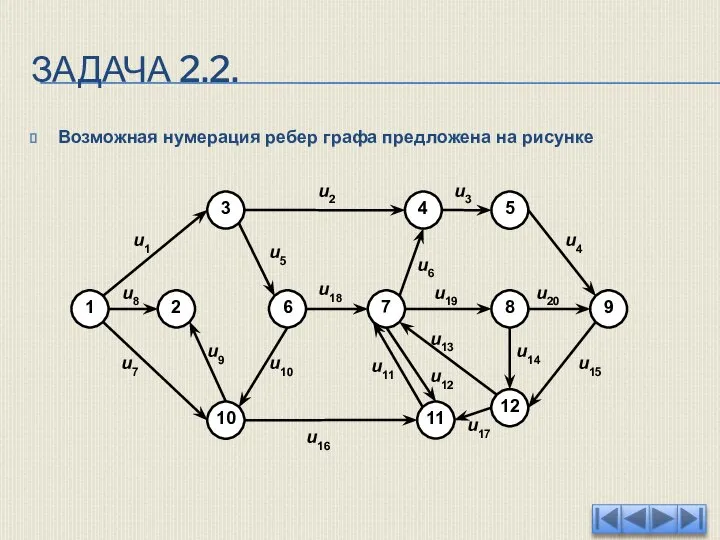
ЗАДАЧА 2.2.
Возможная нумерация ребер графа предложена на рисунке

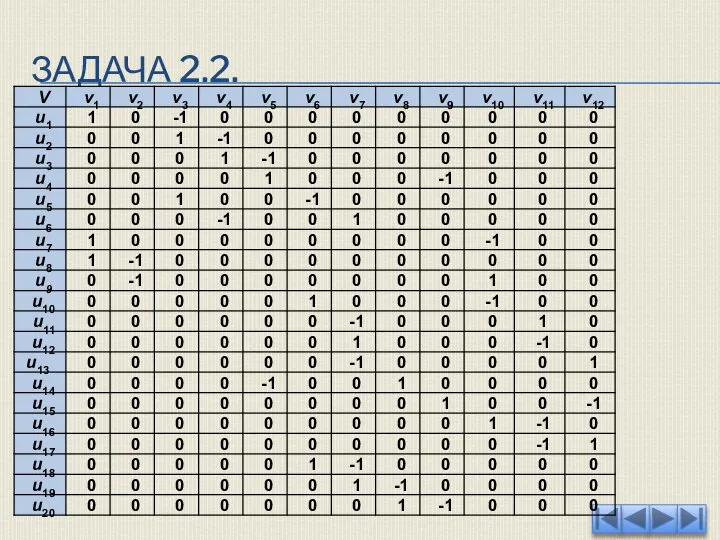
ЗАДАЧА 2.2.
Далее построим матрицу размерности 20 на 12, по строкам перечислив дуги ui, а по столбцам вершины vj.
Рассмотрим вершину v1: она является истоком дуг u1, u7 и u8, поэтому в соответствующих им строках столбца v1 проставляем единицы.
Вершина v3 является истоком дуг u2 и u5 и стоком для дуги u1, поэтому в ячейках матрицы A на пересечении u2, u5 и v3 проставляем единицы, а на перечечении u2 и v3 – минус единицы.
Продолжая такой разбор столбцов для остальных вершин графа, получаем матрицу инциденций, представленную на рисунке ниже.

ЗАДАЧА 2.2.

ЗАДАЧА 2.2.
в) Построение функционального представления.
Функциональные представления графа и орграфа также отличаются. Если неориентированный граф полностью характеризуется функцией Г, то для ориентированного графа необходимо ввести функцию Г1(vi), характеризующую исток вершины vi, и функцию Г-1(vi), характеризующую сток вершины vi.
Функциональное представление достаточно просто строится с помощью графического задания этого графа.
Но наиболее простым путем здесь будет построение с помощью матрицы смежности.
Не сложно заметить, что строкам матрицы смежности соответствует функция Г1(vi), а столбцам - Г-1(vi).

ЗАДАЧА 2.2.
Таким образом получаем, что:
Г1(v1) = {v2, v3, v10}; Г-1(v1) = ∅;
Г1(v2) = {v3}; Г-1(v2) = {v1, v10};
Г1(v3) = { v4, v6}; Г-1(v3) = {v1, v2};
Г1(v4) = {v5}; Г-1(v4) = {v3, v7};
Г1(v5) = {v9}; Г-1(v5) = {v4};
Г1(v6) = {v10}; Г-1(v6) = {v3};
Г1(v7) = {v4, v8, v11}; Г-1(v7) = {v11, v12};
Г1(v8) = {v9, v12}; Г-1(v8) = {v7};
Г1(v9) = {v12,}; Г-1(v9) = {v5, v8};
Г1(v10) = {v2, v11}; Г-1(v10) = {v1, v6};
Г1(v11) = {v11}; Г-1(v11) = {v7, v12,};
Г1(v12) = {v7, v11}; Г-1(v12) = {v8, v12}.

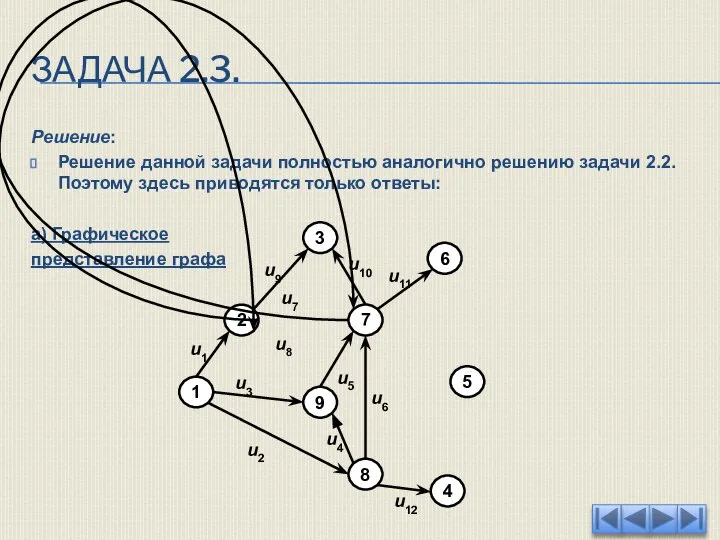
ЗАДАЧА 2.3.
Дан ориентированный граф, заданный матрицей инциденций:
Задать этот граф тремя другими способами: графически, с помощью матрицы смежности, с помощью функционального представления.

ЗАДАЧА 2.3.
Решение:
Решение данной задачи полностью аналогично решению задачи 2.2. Поэтому здесь приводятся только ответы:
а) Графическое
представление графа

ЗАДАЧА 2.3.
б) Матрица смежности графа.

ЗАДАЧА 2.3.
в) Функциональное представление графа:
Г1(v1) = {v2, v8, v9}; Г-1(v1) = ∅;
Г1(v2) = {v3, v7}; Г-1(v2) = {v1, v7};
Г1(v3) = ∅; Г-1(v3) = {v2, v7};
Г1(v4) = ∅; Г-1(v4) = {v8};
Г1(v5) = ∅; Г-1(v5) = ∅;
Г1(v6) = ∅; Г-1(v6) = {v7};
Г1(v7) = {v2, v3, v6}; Г-1(v7) = {v2, v8, , v9};
Г1(v8) = {v4, v7, v9}; Г-1(v8) = { v1};
Г1(v9) = {v7}; Г-1(v9) = {v1, v8}.

ЗАДАЧА 2.4.
Дан неориентированный граф, заданный матрицей смежности:
Задать этот граф тремя другими способами: графически; с помощью матрицы инциденций; с помощью функционального представления.

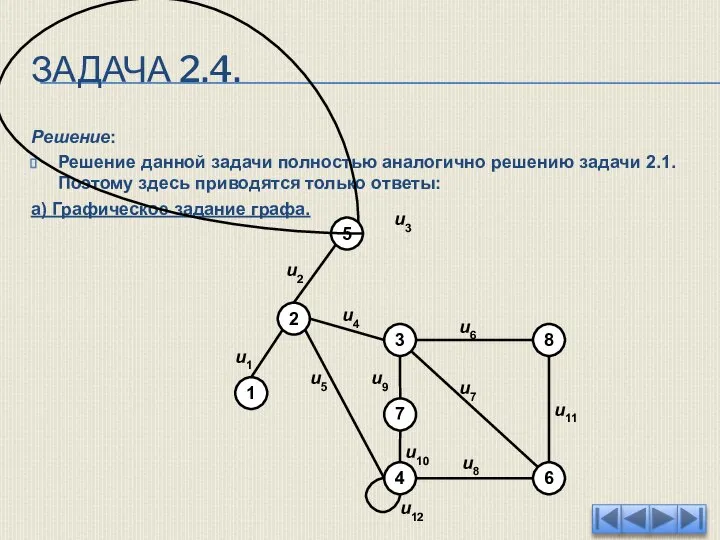
ЗАДАЧА 2.4.
Решение:
Решение данной задачи полностью аналогично решению задачи 2.1. Поэтому здесь приводятся только ответы:
а) Графическое задание графа.

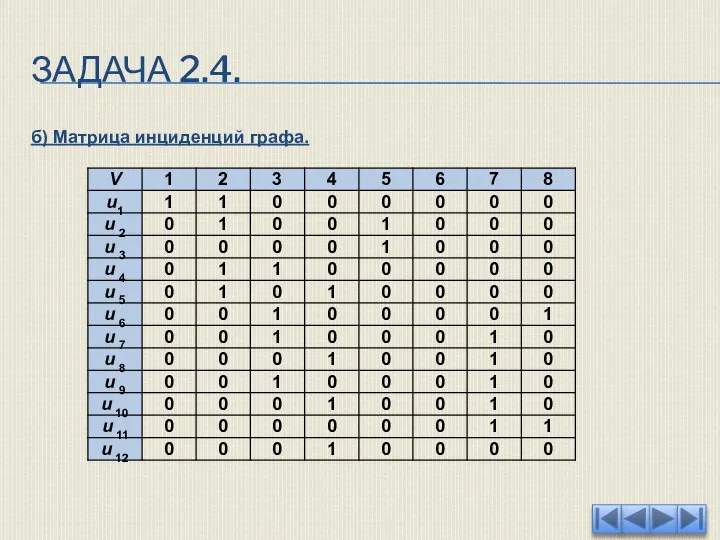
ЗАДАЧА 2.4.
б) Матрица инциденций графа.

ЗАДАЧА 2.4.
в) Функциональное представление графа:
Г(v1) = {v1, v1};
Г(v2) = {v1, v3, v4, v5};
Г(v3) = {v1, , v6, v7, v8};
Г(v4) = {v2, v4, v6, v7};
Г(v5) = {v2, v5};
Г(v6) = {v3, v4, v8};
Г(v7) = {v3, v4};
Г(v8) = {v3, v6}.

РЕШЕНИЕ ЗАДАЧ: СОВЕТЫ И ЗАМЕЧАНИЯ
Решение любой задачи на графы лучше начинать с построения графического представления исходного графа.
Необходимо быть очень осторожным при определении количества вершин, образующих граф, так как некоторые вершины могут быть несвязанными с другими вершинами.
Вершины в графическом представлении графа лучше располагать так, чтобы пересекалось как можно меньше ребер и дуг, а сами вершины были сгруппированы по некоторому признаку подобия.
Матрица смежности неориентированного графа симметрична относительно главной диагонали, в то время как матрица смежности ориентированного графа имеет, вообще говоря, произвольный вид.