Содержание
- 2. Цели урока: Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на
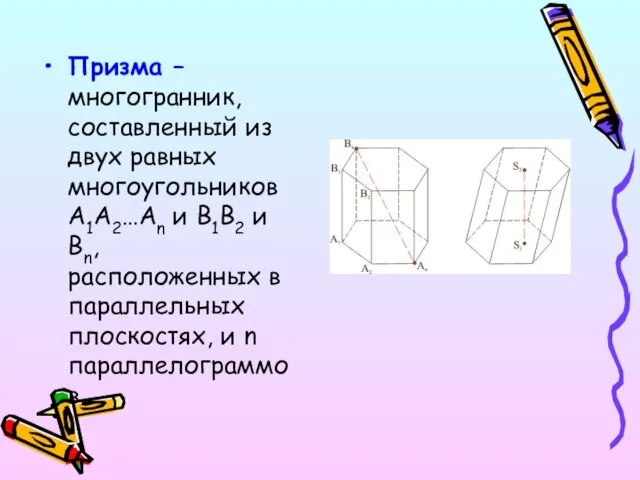
- 3. Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных
- 4. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. Прямая призма называется правильной, если
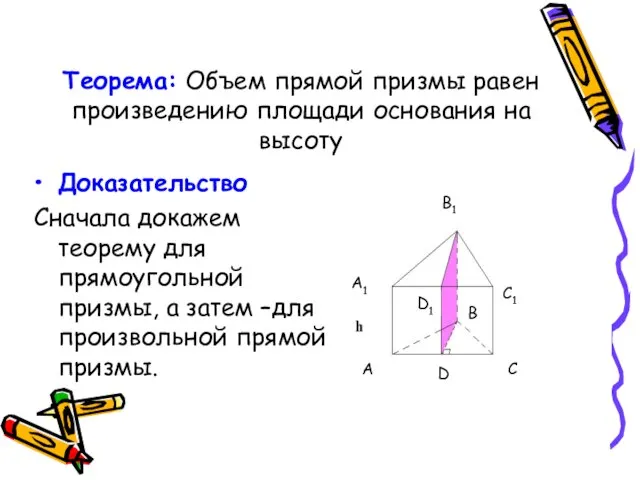
- 5. Теорема: Объем прямой призмы равен произведению площади основания на высоту Доказательство Сначала докажем теорему для прямоугольной
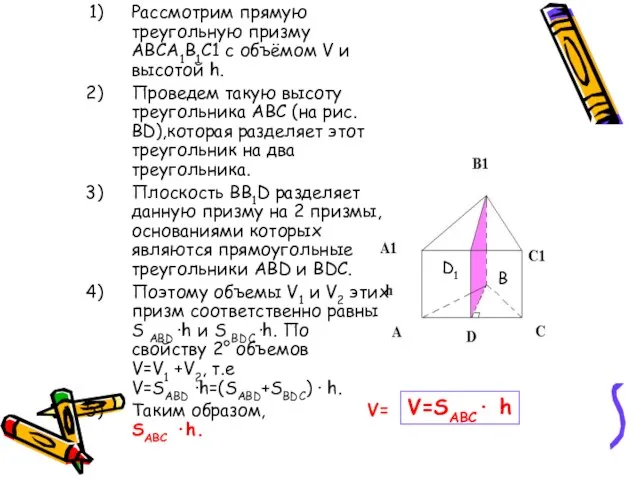
- 6. Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h. Проведем такую высоту треугольника ABC
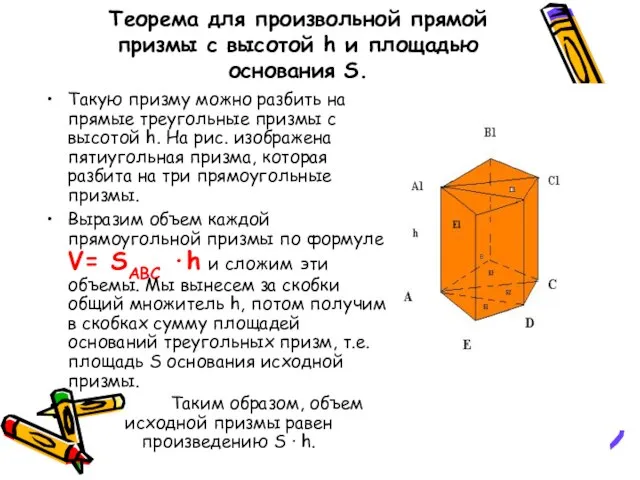
- 7. Теорема для произвольной прямой призмы с высотой h и площадью основания S. Такую призму можно разбить
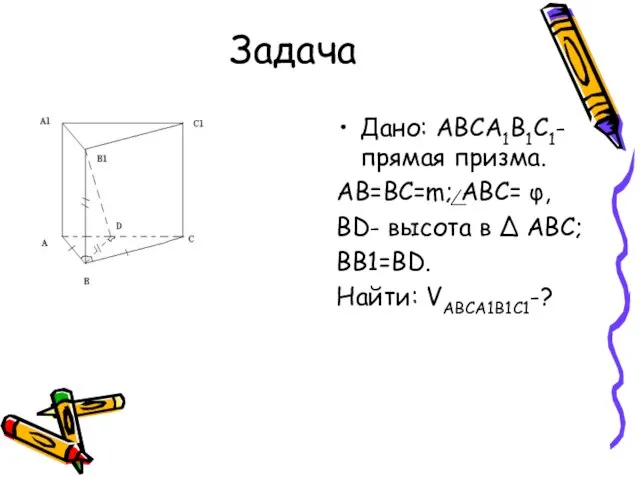
- 8. Задача Дано: ABCA1B1C1- прямая призма. AB=BC=m; ABC= φ, BD- высота в ∆ ABC; BB1=BD. Найти: VABCA1B1C1-?
- 9. Решение: S ABC ·h, h=BB1. Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота ∆ ABC, следовательно
- 10. Вопросы: Как найти объем прямой призмы? Основные шаги при доказательстве теоремы прямой призмы?
- 11. Работу выполнили: Шахбазян Эллена,11”В” Шмырева Юлия,11 “В” Двадненко Аня,11 “В”
- 13. Скачать презентацию





 Многоугольники в окружающем нас мире
Многоугольники в окружающем нас мире Сложение и вычитание векторов
Сложение и вычитание векторов Найдите все значения параметра a,
Найдите все значения параметра a, Применение комбинаторики и бинома Ньютона в теории вероятности
Применение комбинаторики и бинома Ньютона в теории вероятности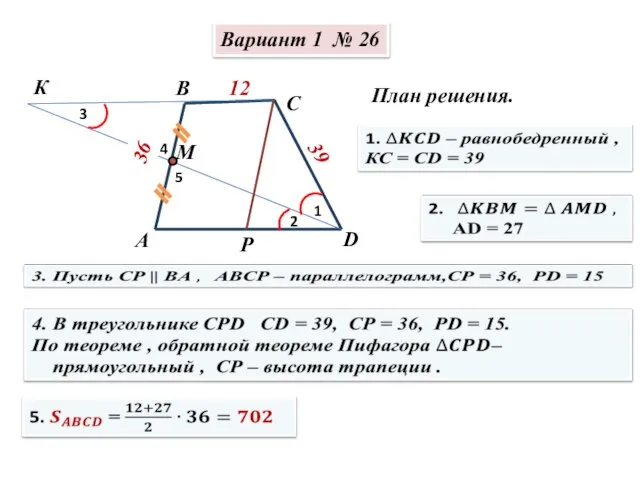 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Изучение конструкции в геометрии токарного резца
Изучение конструкции в геометрии токарного резца Биномиальное распределение
Биномиальное распределение Решение задания В8. Основные типы заданий
Решение задания В8. Основные типы заданий Суммы чисел
Суммы чисел Исследование функции на монотонность и экстремумы
Исследование функции на монотонность и экстремумы К разговору о пропорциях
К разговору о пропорциях Действия с дробями. Многогранники
Действия с дробями. Многогранники Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Преобразование иррациональных выражений
Преобразование иррациональных выражений Загадочное число
Загадочное число Решение задач на t°С воздуха и АД
Решение задач на t°С воздуха и АД Начала комбинаторики. Перестановки
Начала комбинаторики. Перестановки Презентация на тему Арифметическая прогрессия в древности
Презентация на тему Арифметическая прогрессия в древности  Элементы комбинаторики
Элементы комбинаторики Презентация на тему В царстве квадратных корней
Презентация на тему В царстве квадратных корней  Презентация на тему Определение подобных треугольников (8 класс)
Презентация на тему Определение подобных треугольников (8 класс)  Прямоугольник. Теоремы
Прямоугольник. Теоремы Основы эконометрического моделирования
Основы эконометрического моделирования Длиннее, короче (1 класс)
Длиннее, короче (1 класс) Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося
Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося Остановка Задачкино
Остановка Задачкино Возведение в степень. Диктант
Возведение в степень. Диктант