Содержание
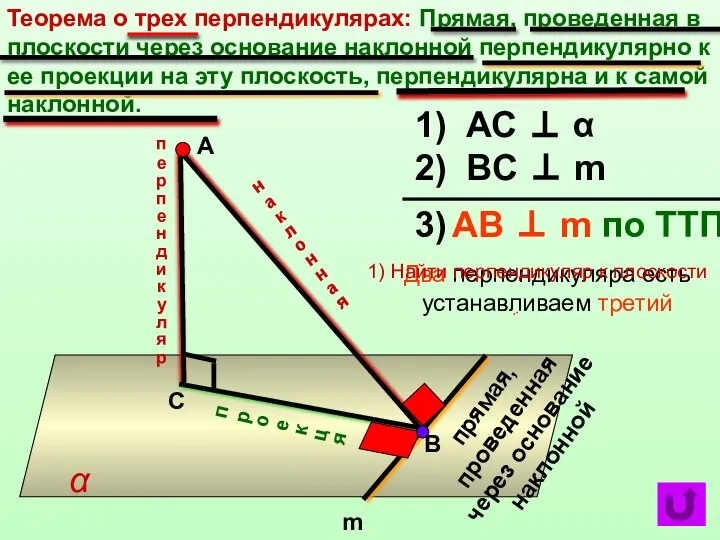
- 2. Теорема о трех перпендикулярах: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на
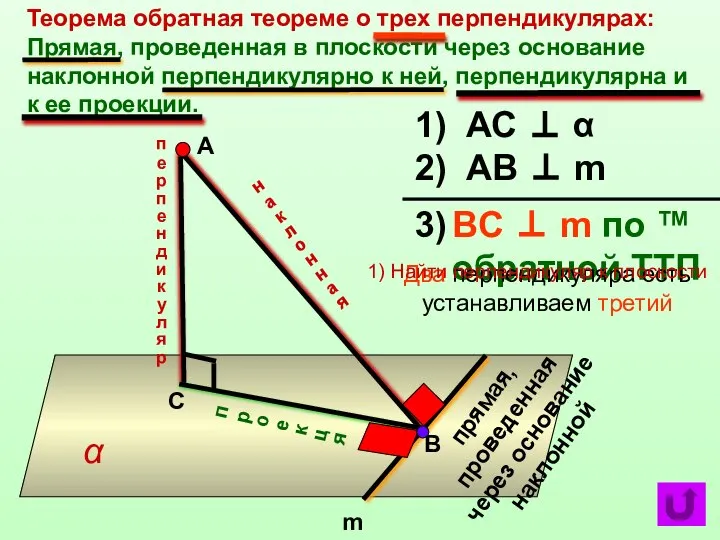
- 3. Теорема обратная теореме о трех перпендикулярах: Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней,
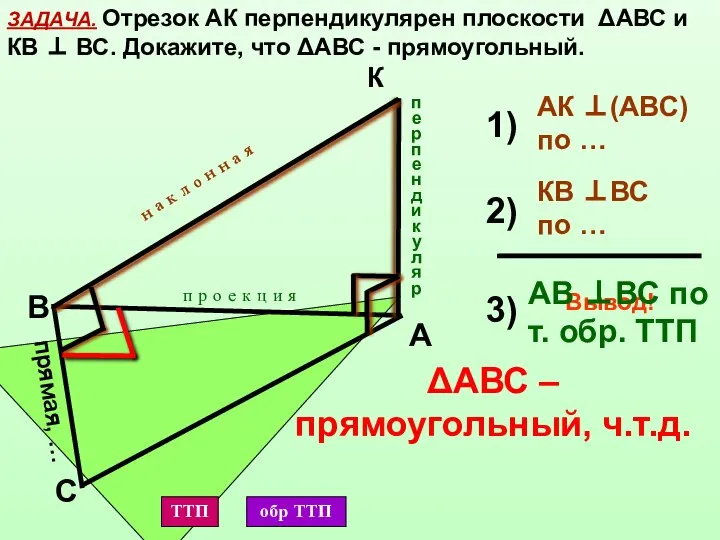
- 4. ЗАДАЧА. Отрезок АК перпендикулярен плоскости ΔАВС и КВ ⊥ ВС. Докажите, что ΔАВС - прямоугольный. А
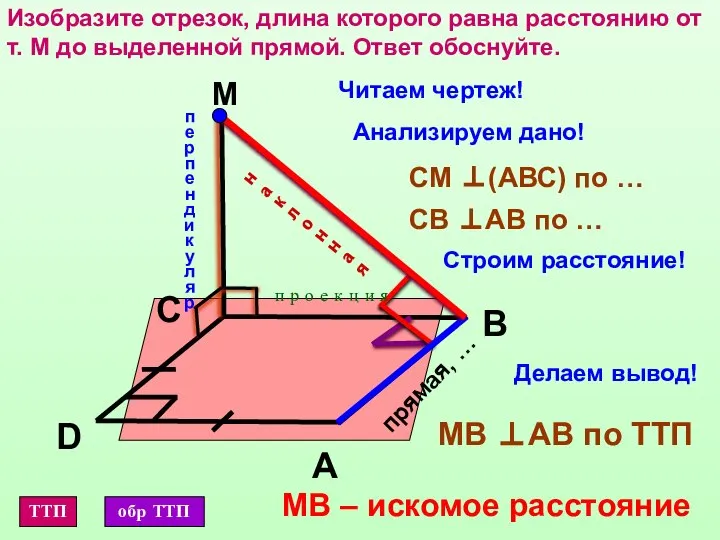
- 5. Изобразите отрезок, длина которого равна расстоянию от т. М до выделенной прямой. Ответ обоснуйте. М D
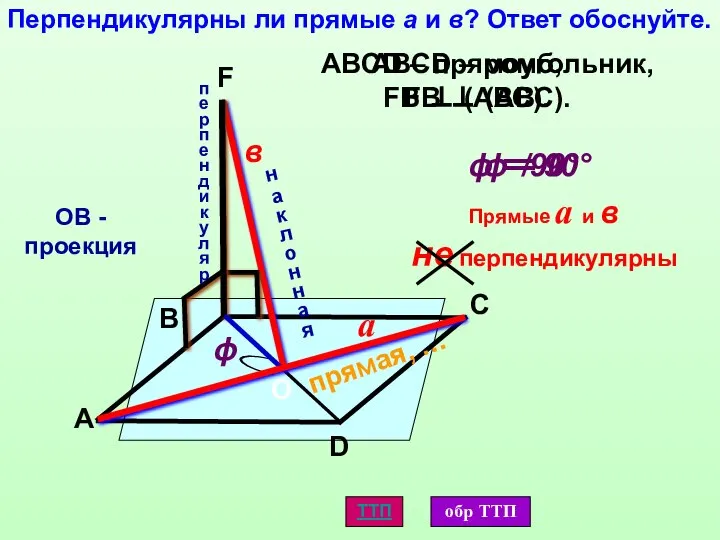
- 6. Перпендикулярны ли прямые а и в? Ответ обоснуйте. а в D А С В F ABCD
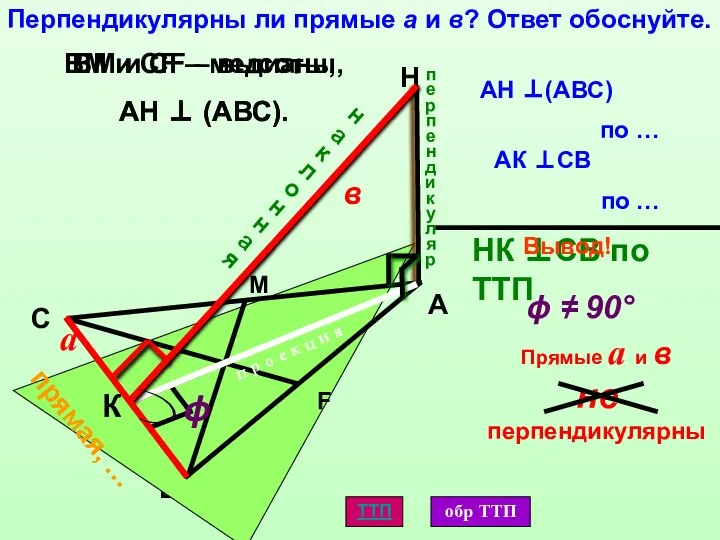
- 7. К А В С H Перпендикулярны ли прямые а и в? Ответ обоснуйте. BM и CF
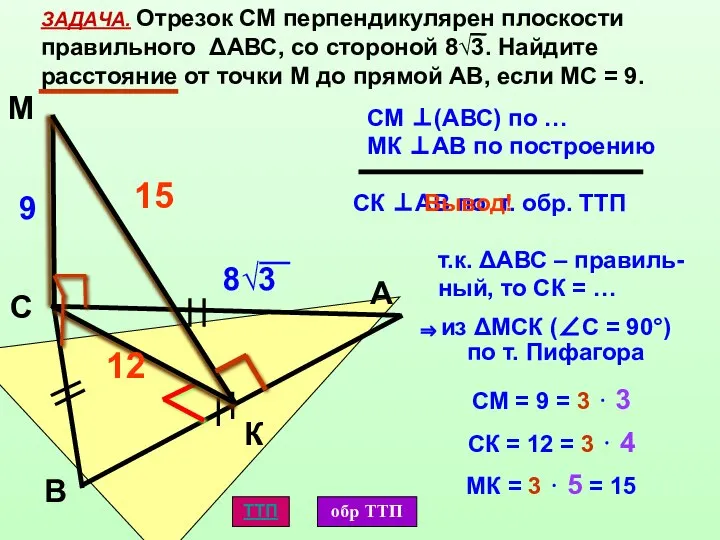
- 8. К М С А В ЗАДАЧА. Отрезок СМ перпендикулярен плоскости правильного ΔАВС, со стороной 8√3. Найдите
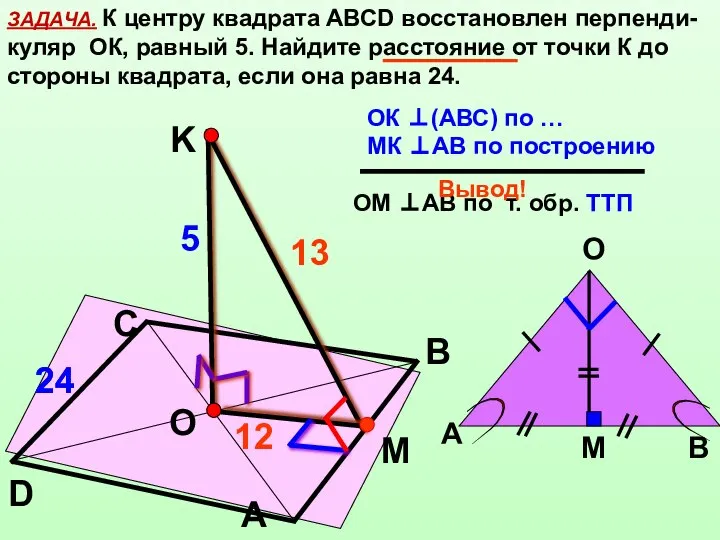
- 9. ЗАДАЧА. К центру квадрата АВСD восстановлен перпенди-куляр ОК, равный 5. Найдите расстояние от точки К до
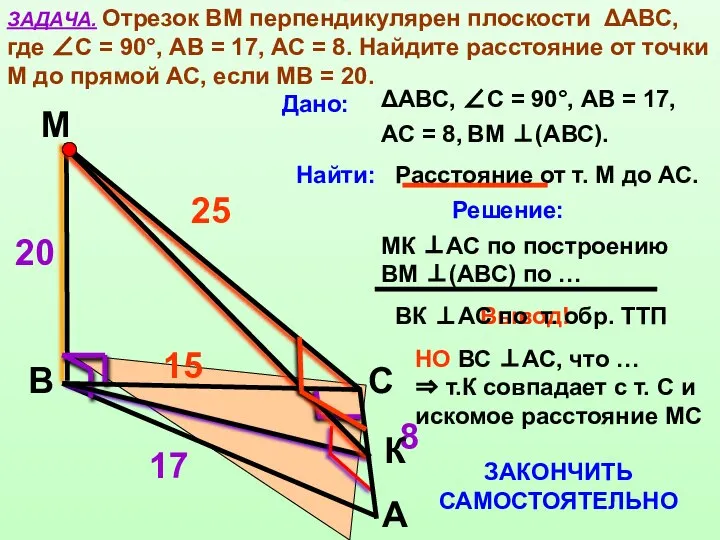
- 10. ЗАДАЧА. Отрезок ВМ перпендикулярен плоскости ΔАВС, где ∠С = 90°, АВ = 17, АС = 8.
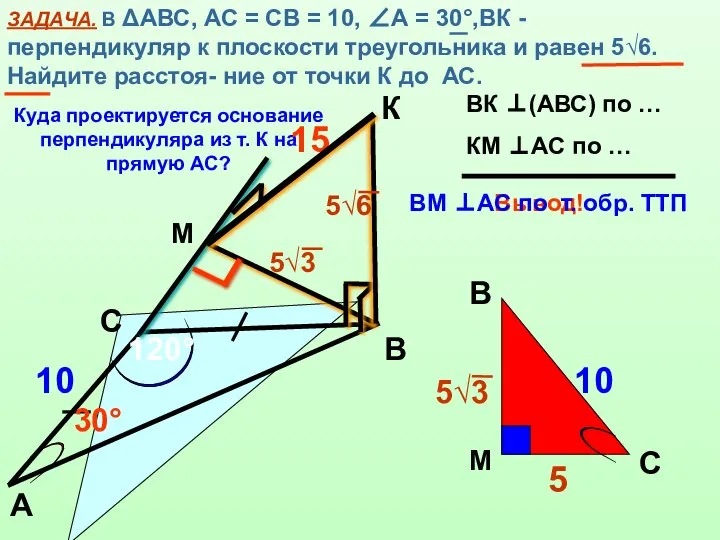
- 11. ЗАДАЧА. В ΔАВС, АС = СВ = 10, ∠А = 30°,ВК - перпендикуляр к плоскости треугольника
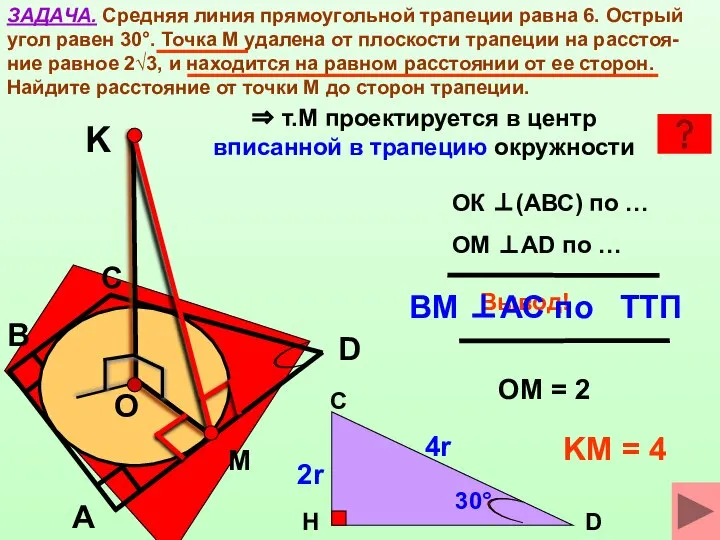
- 12. ЗАДАЧА. Средняя линия прямоугольной трапеции равна 6. Острый угол равен 30°. Точка М удалена от плоскости
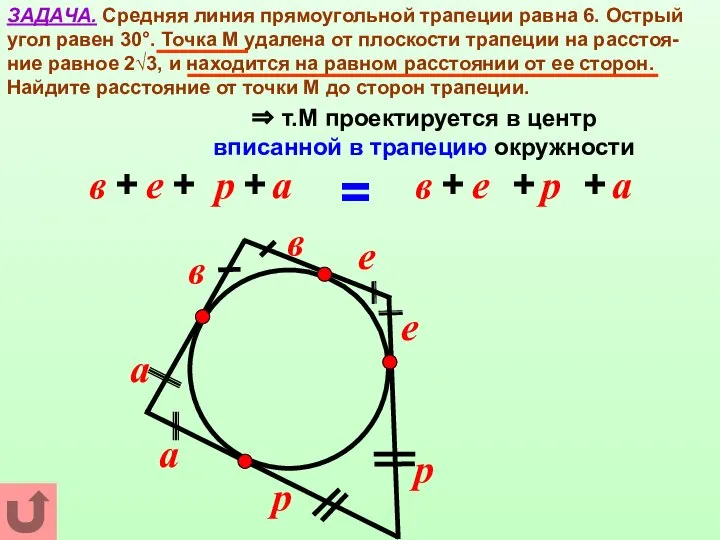
- 13. ЗАДАЧА. Средняя линия прямоугольной трапеции равна 6. Острый угол равен 30°. Точка М удалена от плоскости
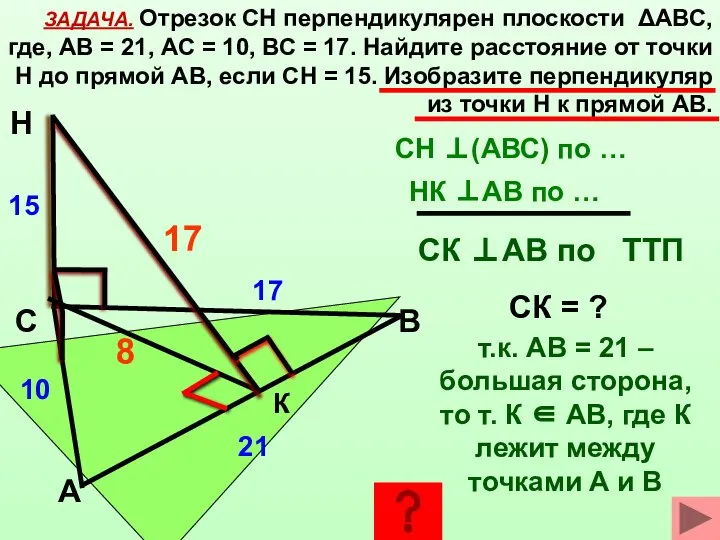
- 14. ЗАДАЧА. Отрезок СН перпендикулярен плоскости ΔАВС, где, АВ = 21, АС = 10, ВС = 17.
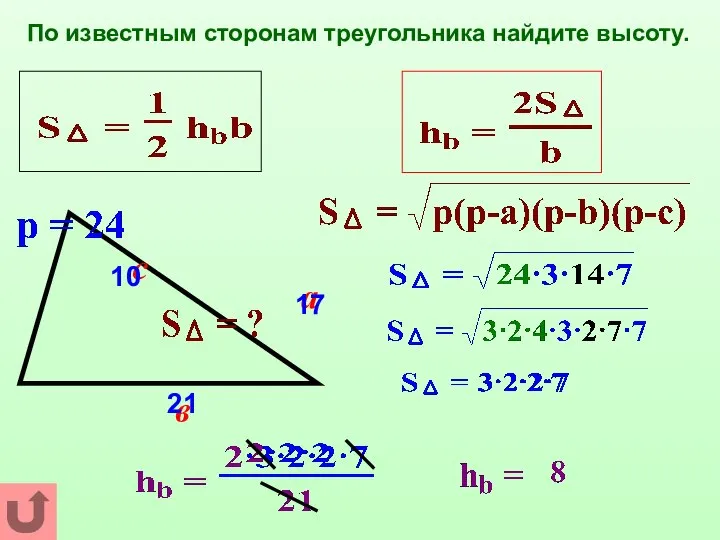
- 15. По известным сторонам треугольника найдите высоту. а с в 10 17 21
- 17. Скачать презентацию
 Задача на процкеты
Задача на процкеты Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Построение сечений
Построение сечений Функции и графики
Функции и графики Степенные функции
Степенные функции Моделирование на графах
Моделирование на графах Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед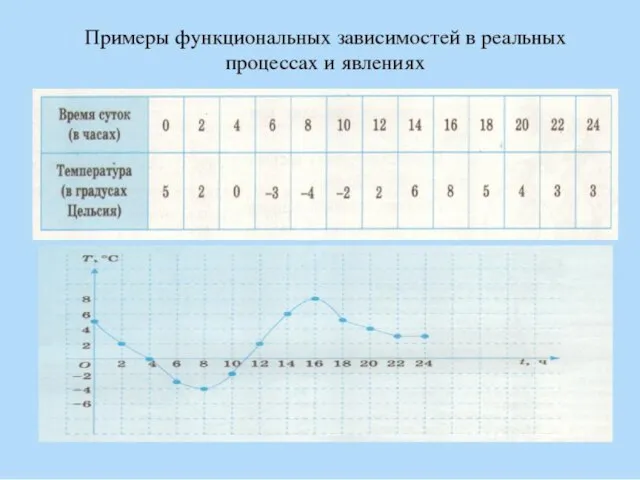 График функции. Примеры
График функции. Примеры В мире рациональных уравнений
В мире рациональных уравнений Возникновение слова “процент”. Древний Рим
Возникновение слова “процент”. Древний Рим Аксиомы планиметрии (часть 2)
Аксиомы планиметрии (часть 2) Квадратные корни
Квадратные корни Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики
Урок по учебнику Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков Алгебра 9 с углубленным изучением математики Делители и кратные
Делители и кратные Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Решение логических задач
Решение логических задач Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль) Признаки параллельности двух прямых
Признаки параллельности двух прямых Золотое сечение (продолжение)
Золотое сечение (продолжение) Сфера и шар. Уравнение сферы
Сфера и шар. Уравнение сферы Математика на кухне
Математика на кухне Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Усовершенствование навыков действий с рациональными числами
Усовершенствование навыков действий с рациональными числами Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Исследование функции
Исследование функции Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения