Теория множеств

Эпиграф
В любых делах при максимуме сложностей
Подход проблеме все-таки один:
Желанье – это множество возможностей,
А нежеланье – множество причин.
Эдуард Асадов

История появления
Теория множеств возникла в результате реализации программы стандартизации математики, разработанной немецким математиком Георгом Кантором (1845–1918).
Множество есть «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью»
Георг Кантор (1845–1918)

История появления
Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного», 1850). В этой работе рассматриваются произвольные (числовые) множества, и для их сравнения определено понятие взаимно-однозначного соответствия.
Бернард Больцано (1781–1848)

История появления
В XVIII веке Леонард Эйлер использовал круги в качестве наглядно-графическое изображение множества
Леонард Эйлер (1707–1783)
“…Эти круглые фигуры, или, вернее, пространства способны облегчить ход наших рассуждений, а также позволяют нам раскрыть все тайны, которыми похваляется логика. С помощью этих символов всё сразу бросается в глаза…”

История появления
Джон Венн (1834–1923)
В XIX веке сходное изображение множеств использовал английский логик Джон Венн.
Он изображал множества прямоугольниками, и использовал эти изображения для доказательства утверждений о множествах

Задание
Приведите житейские названия следующих множеств:
1) множество марок, принадлежащих одному человеку;
2) множество пчел, летящих вместе;
3) множество цветных карандашей в коробке;
4) множество военных, подчиняющихся одному командиру; 5) множество футболистов, собравшихся вместе для игры; 6) множество цветов, в руке первоклассницы.
Что во всех этих случаях вы понимаете под множеством?

Понятие множества
«Множество есть многое, мыслимое как единое целое»
Множество - совокупность объектов, определяемых некоторым свойством, присущим каждому из них.
Каждый объект, входящий в множество, называется его элементом, а свойство их объединяющее – характеристическим свойством множества.

Символы и обозначения
А, В, С, D, … – множества
a, b, с, d, … – элементы множества
При записи множества перечислением его элементов используют символ «{ }».
– символ принадлежности элемента множеству
– пустое множество

Мощность множества
Мощностью конечного множества называется количество его элементов.
Обозначение |A|.

1) перечисление всех его элементов.
A={студент А., рабочий Л., школьник М.}
2) указание общего свойства элементов
В - множество четных натуральных чисел.
В = {b| b = 2k, k — любое натуральное число}.
3) Символьное обозначение
N – множество натуральных чисел
Z – множество целых чисел
Q – множество рациональных чисел
R – множество действительных чисел
I – множество иррациональных чисел
4) Указание концов числового промежутка
[2; 8], (0; 6,5)
Способы задания множеств

1
0
–1
Способы задания множеств
Задайте множество всех целых чисел, удовлетворяющих неравенству :
a) перечислением элементов;
б) заданием характеристического свойства;
в) изображением на координатной прямой.
{–1; 0; 1}

Задание
Измените способ задания множества: а) А – множество всех цифр. б) В =
. в) С =
.

Задание

Отношения между множествами
Множества A и B называются равными, если они состоят из одних и тех же элементов. Обозначение: A=B.
{a, b, c, d} = {c, b, a, d}

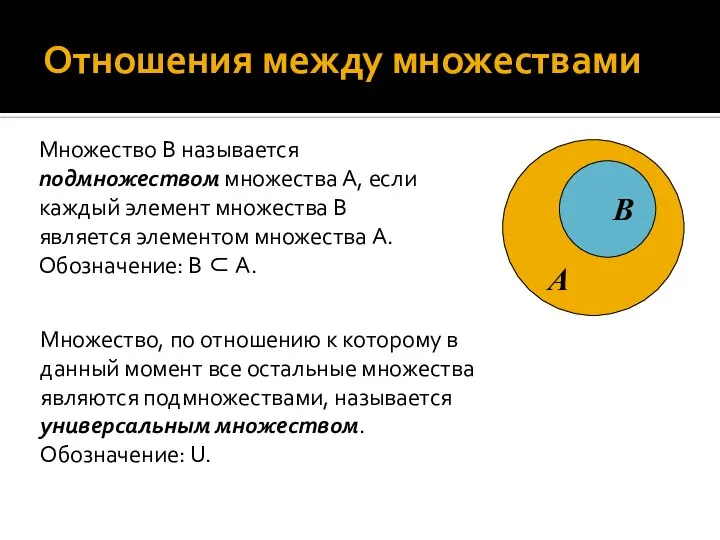
Отношения между множествами
Множество B называется подмножеством множества A, если каждый элемент множества B является элементом множества A. Обозначение: B ⊂ A.
В
А
Множество, по отношению к которому в данный момент все остальные множества являются подмножествами, называется универсальным множеством. Обозначение: U.

Задание

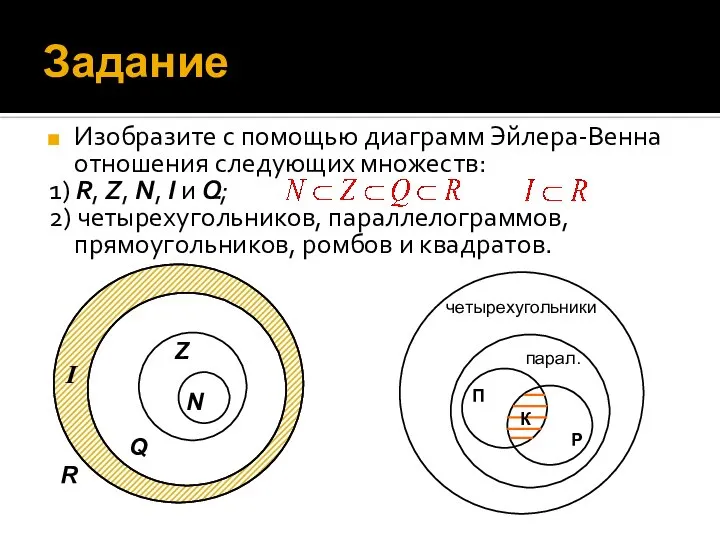
Задание
Изобразите с помощью диаграмм Эйлера-Венна отношения следующих множеств:
1) R, Z, N, I и Q;
2) четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов.
N
Z
Q
R
четырехугольники
парал.
П
Р
К

Задание
Установите соответствие между множествами и верными для них высказываниями.

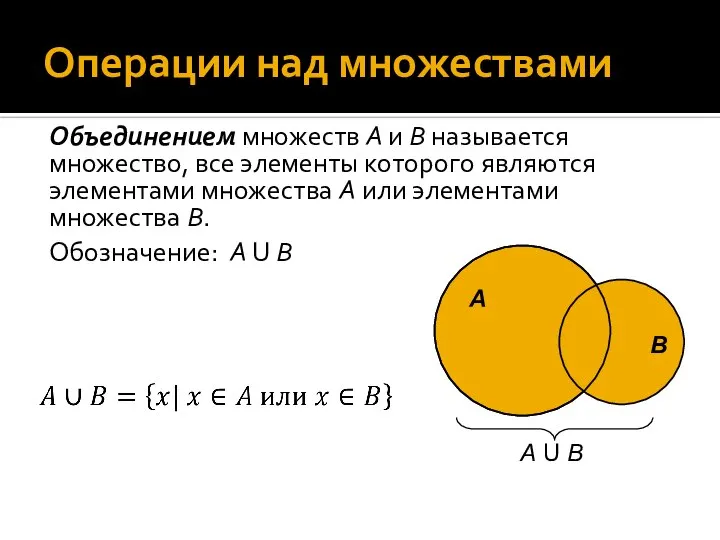
Операции над множествами
Объединением множеств А и В называется множество, все элементы которого являются элементами множества А или элементами множества В.
Обозначение: А U B
А
В
А U В

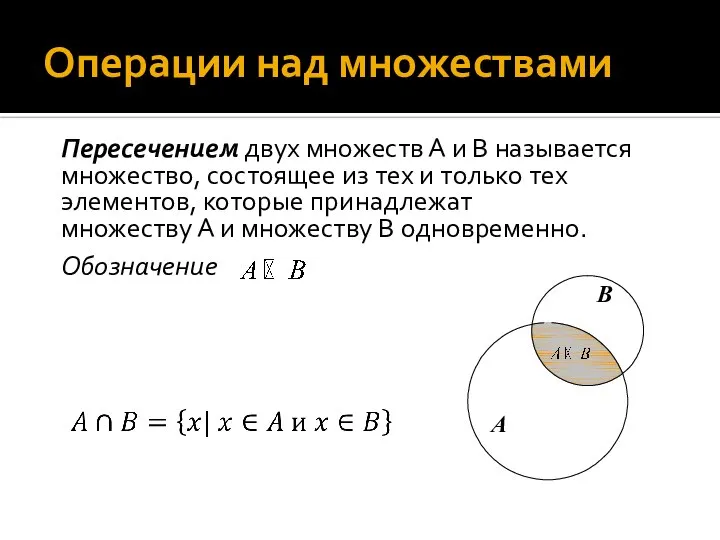
Операции над множествами
Пересечением двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат
множеству А и множеству В одновременно.
Обозначение

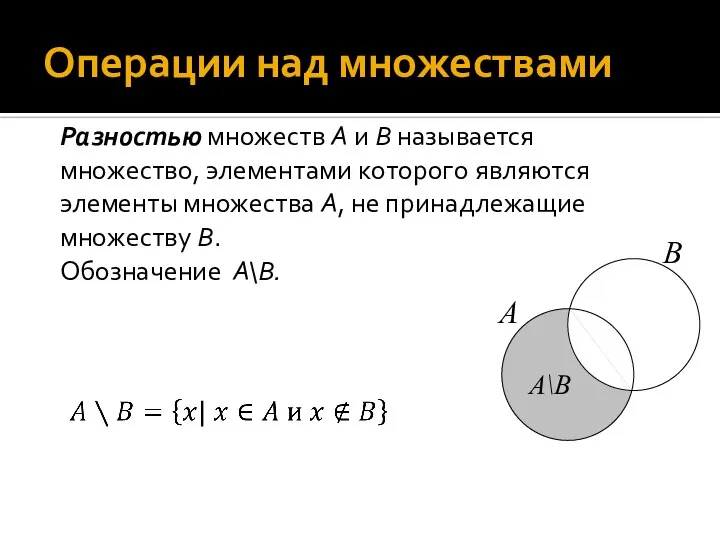
Операции над множествами
Разностью множеств А и В называется множество, элементами которого являются элементы множества А, не принадлежащие множеству В.
Обозначение А\В.
А\B
А
В

Операции над множествами
Дополнением к множеству A называется разность между универсальным множеством и множеством A.

Задание

Задание

Задание

Задание
В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на коньках и на лыжах?

Задание
Каждая из 30 невест, зарегистрированных
в клубе знакомств, красива, воспитана или умна. Воспитанных невест – 21, красивых – 18,
умных – 15. Красивых и воспитанных – 11,
умных и воспитанных – 9, умных и красивых – 7. Сколько невест обладает всеми тремя качествами?
В – множество воспитанных невест
К – множество красивых невест
У – множество умных невест

Решение
В – множество воспитанных невест
К – множество красивых невест
У – множество умных невест
У
В
К
15
21
18
|B|=21, |K|=18, |У|=15
х
21 + 18 + 15 – 9 – 11 – 7 + х = 30
11
9
7
|В ∪ К ∪ У| = 30
х + (9 – х) + (7 – х) + (11 – х) +
+ (15 – 7 – (9 – х)) + (18 – 11 – (7 – х)) + (21– 9 – (11 – х))
= 30
х = 3