История системы мер длины (часть 1)

… вначале было три параллельных процес-са:
создание универсальной системы мер длины
изучение секундного маятника
измерение размеров Земли с помощью триангуляций…
Но постепенно они стали сходиться вместе и тогда появился современный «метр»!

История термина «метр»
В 1675 г. в трактате «Misura Universale» Тито Ливио Бураттини (Tito Livio Burattini; 1617…81) предложил принять для всей Ев-ропы новый метрологический базис. Эту меру Бураттини назвал «метр» (metro cattolico, то есть «универсальная мера»).
8 мая 1790 г. Национальным собранием Франции было одобре-но предложение будущего всесильного дипломата Талейрана (Charles Maurice de Talleyrand-Périgord; 1754…1838) создать но-вую систему мер Революционной Франции по образу системы Бураттини.
Эталон новой системы мер назвали «метром» («mètre»).

История десятеричной системы мер
В 1675 г. в трактате «Misura Universale» Тито Ливио Бураттини предложил принять для всей Европы новую систему мер, в кото-рой все соседние меры соотносились бы друг с другом как 1:10.
8 мая 1790 г. Национальным собранием Франции было одобре-но предложение Талейрана создать новую систему мер Револю-ционной Франции по образу системы Бураттини.
30 марта 1791 г. Французское Национальное собрание с подачи Жана-Шарля де Борда (Jean-Charles, chevalier de Borda; 1733…99) решило поделить окружность на 400 «градов», по 100 в каждой четверти.

История математического маятника
На рубеже XVI и XVII вв. Галилео Галилей (Galileo Galilei; 1564…1642) разработал общие положения теории математичес-кого маятника.
В 1644 г. Марен Мерсенн (Marin Mersenne; 1588…1648) впер-вые определил длину секундного маятника (сегодня это 0,994 м при g = 9,80665 м/с2).
А в 1660 г. Лондонское королевское общество (академия наук) предложило использовать длину секундного маятника в качест-ве универсальной стандартной единицы длины.
В 1671 г. Жан Рише (Jean Richer; 1630…96) обнаружил, что в Кайенне (Cayenne; 4°56′ с. ш. 52°20′ з. д.) секундный маятник, настроенный в Париже, стал отставать на 2 мин. в сутки.
Его пришлось укорачивать (на 0,3%).

История математического маятника (продолжение)
В 1687 г. Исаак Ньютон (sir Isaac Newton; 1642…1727) высказал гипотезу о Полюсном сжатии: полюсный радиус планеты по-лучился у него на 1/230 короче экваториального (сейчас этот эф-фект оценивается в составляет 1/298, 257...). Ньютон считал, что таким образом объясняется эффект замедления секундного ма-ятника, обнаруженный Рише.
В дальнейшем наблюдения Рише и теория Ньютона были неод-нократно подтверждены наблюдениями других учёных.
8 мая 1790 г. Национальным собранием Франции было одобре-но предложение Талейрана приравнять метр секундному маят-нику.
В 1675 г. Тито Ливио Бураттини предложил принять приравнять metro cattolico секундному маятнику. Бураттини оценил длину metro cattolico в 4 пальмы Генуи (996,38 мм).

История математического маятника (окончание)
30 марта 1791 г. Французское Национальное собрание с подачи Жана-Шарля де Борда решило поделить окружность на 400 «градов», по 100 в каждой четверти.
На 1 град земного меридиана должно было идти ровно 100 000 метров (40 000 000 м на весь меридиан). От маятника отказа-лись!

История «геодезических» мер
Ещё средневековые арабы знали, что древнеримская миля, mille passuum, укладывалась в градус меридиана ровно 75 раз.
Эта оценка вполне подтверждается фактами, но как это удалось древним римлянам современная наука не знает!
Джироламо Кардано (Gerolamo Cardano; 1501…76), изучив све-дения о научных взглядах Пифагора, пришел к выводу, что абсо-лютно точные научные знания о форме и размерах Земли были известны ещё в Древнем Египте: египтяне якобы создали свои меры из природных констант и зафиксировали свои знания о размерах нашей планеты в Пирамиде Хеопса.

История «геодезических» мер (окончание)
30 марта 1791 г. Французское Национальное собрание с подачи Жана-Шарля де Борда решило поделить окружность на 400 «градов», по 100 в каждой четверти.
На 1 град земного меридиана должно было идти ровно 100 000 метров (40 000 000 м на весь меридиан).
Однако ещё в 1613 г. на карте Меркатора было указано, что «ми-ля Франции» (Miliaria Gallica communia) укладывается в градус меридиана ровно 20 раз!
В 1674 г. – по итогам градусного измерения Пикара – были уточнены протяженности французских путевых мер, сухопут-ного и морского льё: 25 и 20 в градусе меридиана соответствен-но.

История триангуляций
В 1530 г. Гемма Фризиус (Gemma Frisius; 1508…55) разработал теорию метода триангуляций.
Первые в современной истории градусные измерения выполнил в 1615 г. Виллеброрд Снелл (Снеллиус; Willebrord Snel van Roy-en; 1580…1626). Снелл триангулировал дугу меридиана в 1°11′30″ в Нидерландах между Берген-оп-Зомом и Алкмаром.
Полученная им оценка протяженности одного градуса мериди-ана была на 3,57% меньше современной.
В 1669…70 гг. Жан-Феликс Пикар (Jean-Felix Picard; 1620…82) измерил протяженность дуги меридиана между Парижем и Амь-еном (1°04′, 13 треугольников). Измерения Пикара были очень точными (сегодня их погрешность оценивается в 0,03% и даже в меньшую величину).

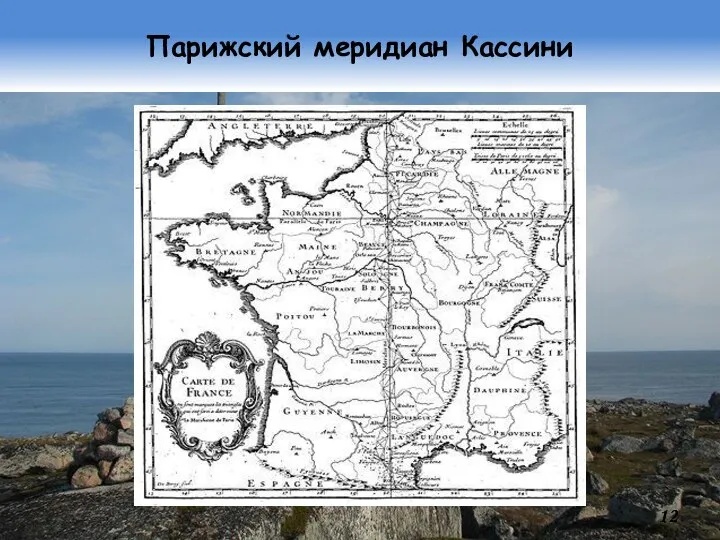
История триангуляций (продолжение)
В 1683 г. Джованни Доменико Кассини (ит. Giovanni Domenico Cassini; фр. Jean-Dominique Cassini; 1625…1712) продолжил ра-боту Пикара: триангуляцию Парижского меридиана предстояло продлить до Дюнкерка на севере и до побережья Средиземного моря на юге (всего 8°32′, 54 мерных треугольника).
Джованни Кассини не сумел завершить начатое – это сделал его сын Жак (Jacques Cassini; 1677…1756). Градусные измерения проходили с большими перерывами и были завершены только в 1718 г. Они дали очень странный результат…
Из данных Кассини следовало, что Земля вытянута к полюсам! Это противоречило теории Ньютона, но Кассини-младший не хотел признавать даже возможности ошибки в их с отцом рабо-те!

Парижский меридиан Кассини

История триангуляций (продолжение)
Новый эталон французского «королевского» фута (pied-de-roi) в 1732 г. поручили изготовить граверу Ланглуа (Claude Langlois), которому с тех пор было дано монопольное право производить измерительные линейки для научных работ во всей Франции.
Жак Кассини обвинил Пикара в использовании бракованного эталона меры длины, toise du Châtelet.
Ланглуа выбрал эталон таким, чтобы в кубе с длиной ребра в 1 pied-de-roi, содержалось 70 парижских ливров воды. Новый эта-лон был длиннее того, каким пользовался Пикар, примерно на 0,114%.
Были сформированы 2 экспедиции: одна – на экватор, в Перу, вторая – поближе к Полюсу, в Лапландию. Измерения в Перу (в 1735…42 гг.) и в Лапландии (в 1736 г.) убедительно доказали, что Земля имеет Полюсное сжатие.

История триангуляций (продолжение)
В 1739…41 гг. сын Жака Кассини, Цезарь Франсуа Кассини де Тюри (César-François Cassini de Thury; 1714…84), и Николя Ла-кайль (Nicolas-Louis De la Caille; 1713…62) повторили измере-ния, выполненные старшими Кассини. Прежние расчеты стар-ших Кассини и Пикара были скорректированы с учетом нового эталона. В измерениях старших Кассини было выявлено много мелких ошибок.
В 1750…54 гг., во время своей астрономической экспедиции в Южную Африку, Лакайль выполнил триангуляцию, которая показала, что в Южном полушарии Земля была более плоской, чем в Северном.
Эта ошибка была окончательно устранена только в 1838 г.

Торжество Пикара
К середине XX в. учёные всё же пришли к выводу, что работа Пикара была очень точной.
Если предположить, что Кассини приняли оценку протяженности «Дуги Пикара» без корректировок, то ошибку надо искать в изме-рениях дуги между Амьеном и Дюнкерком: примененный там туаз должен был отличаться от эталонного toise du Châtelet образ-ца 1667 г. на 0,37%, что дает его размер 1 956,26 мм. Отсюда раз-мер «королевского» фута должен был бы быть 326,04 мм.
В Дюнкерке Кассини использовали старый туаз?

История триангуляций (продолжение)
Но 1 августа 1793 г. Конвент принял «временный» эталон мет-ра на основе данных Кассини де Тюри и Лакайля, а работы Де-ламбра и Мишена были приостановлены до 7 апреля 1795 г.
Триангуляция Деламбра и Мешена дала размер метра, незначи-тельно, но отличающийся от уже утвержденного «эталона» (3 парижских фута и 11,296 линии против 3 футов и 11,44 линии, которые были получены из данных Кассини и Лакайля).
Корректировка размера метра была узаконена 10 декабря 1799 г.
В 1792 г. Деламбр (Jean-Baptiste Joseph Delam-bre; 1749…1822) и Мешен (Pierre François André Méchain; 1744…1804) стали пе-ремерять Парижский меридиан (от Дюнкерка до Барселоны).

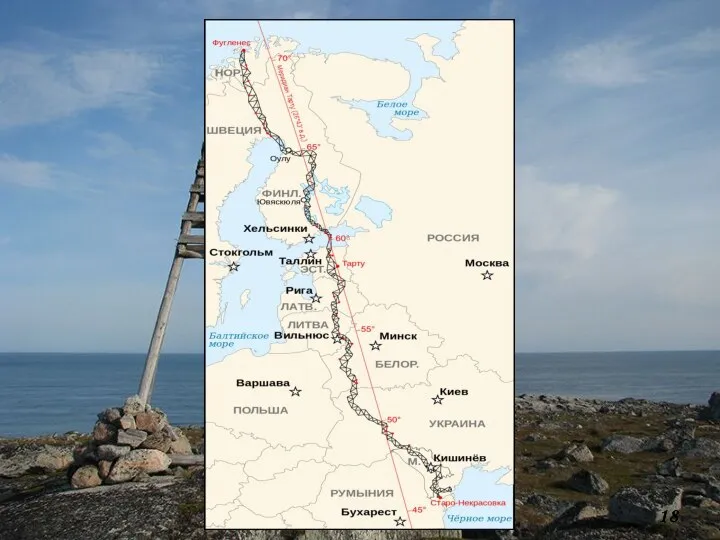
История триангуляций (продолжение)
Самой масштабной триангуляцией в мире долгое время была «Геодезическая дуга Струве»: ее прокладывали с 1816 по 1855 гг. (в течение 40 лет!!!) на протяжении 2 820 км (25°20′08″), от побережья Северного Ледовитого океана (мыс Фугленес, недалеко от мыса Норд-Кап в Норвегии (70°40′11″ с.ш.)), и до устья Дуная (с. Старая Некрасовка в Одесской области Украины (45°20′03″ с.ш.)) под руководством Фридриха Георга Вильгельма (Василия Яковлевича) Струве (1793…1864) и Карла Ивановича Теннера (1783…1860).
Суммарная ошибка этой триангуляции составила смешные… 50 м!

История триангуляций (окончание)
Самая масштабная триангуляция в мире была осуществлена в СССР в 1930…50 гг. под руководством Феодосия Николаевича Красовского (1878…1948): Государственной геодезической сетью триангуляции, была охвачена половина территории СССР, детализация сети сначала соответствовала масштабу 1 : 10 000, а затем была увеличена до 1 : 2 000.
По данным этой сети Александром Александровичем Изотовым (1907…88) в 1940 г. была разработана математическая модель поверхности Земли Референц-эллипсоид Красовского.

Злоключения метра
Для продвижения Метрической системы мер в сентябре 1798 г. был созван Международный конгресс (прибыли только предста-вители союзных Франции стран). Он завершил свою работу 25 мая 1799 г.
… однако осенью 1799 г. к власти пришел Наполеон, а ему но-вая система мер не нравилась…
Не нравилась она и большинству французов…
Потом Франции вообще стало не до «метра»…
Потом не стало самой Наполеоновской Франции…
В итоге метр окончательно утвердился в у себя на родине только в 1840 г. (закон от 4 августа 1837 г.).

Злоключения метра (продолжение)
В процессе разработки первой в истории современной науки ма-тематической модели Земного эллипсоида Ф.В. Бессель (Fried-rich Wilhelm Bessel; 1784…1846) в 1841 г. обнаружил ошибку в вычислениях Деламбра и Мишена.
В 1869 г. было признано, что «архивный» метр утратил «харак-тер естественной меры, который ему приписывался при его изготовлении, и в настоящее время он является просто произ-вольной и условной мерой».
Тем не менее, в 1870 г. в Париже собралась Международная метрическая комиссия (La Commission internationale du mètre), в основу работы которой были положены конструктивные пред-ложения, высказанные в Докладе РИАН в 1869 г.

Злоключения метра (окончание)
Разразившаяся в 1870 г. Франко-прусская война прервала работу Международной метрической комиссии на 2 года.
(В США метрическую систему так и не ввели до сих пор, а в Англии – только в 1995 г.)
Итогом работы Комиссии стала дипломатическая конференция, на которой 20 мая 1875 г. Представители 17 государств подпи-сали Метрическую конвенцию.
Изготовление эталонов метра и килограмма завершилось к 1889 году, когда на I Международной конференции мер и весов эти эталоны были распределены между странами по жребию (Рос-сия получила эталоны метра №28 (сегодня признаётся основ-ным) и №11, а килограмма – №12 (основной) и №26).

Судьба метра в России
04.06.1899 в Российской империи принято «Положение о мерах и весах» (за-кон). Оно разрешало применение в торговых и иных операциях наравне с российскими мерами, также и (по соглашению сторон) мер Метрической сис-темы.
30.04.1917 принят декрет Временного правительства об обязательном при-менении Метрической системы на территории России. По понятным причи-нам, он не был воплощен в жизнь…
Декрет СНК РСФСР от 11.09.1918 инициировал переход страны на Метри-ческую систему.
Декрет СНК РСФСР от 29.05.1922 актуализировал сроки этого перехода.
С 1 октября 1924 г. прекратилось изготовление мерного инвентаря старой русской системы мер.
С 1 января 1925 г. Метрическую систему начали вводить в Советских уч-реждениях.
С 1 января 1927 г. Метрическая система стала обязательной в СССР.

Прощай, триангуляция!
Модель Красовского и Изотова стала последней, полученной классическим наземным методом: в дальнейшем масштабные геодезические исследования стали осуществляться с помощью космических аппаратов.
И эти исследования, в частности, показали, что Референц-эллипсоид Крассовского оказался предельно точным: погрешность оценки его большой полуоси составила всего 1,7 * 10-5, а оценка сжатия полностью совпала с реальностью.