Содержание
- 2. Дифференциальные уравнения Определение Уравнение, связывающее независимую переменную x с неизвестной функцией y(x) и ее производными до
- 3. Дифференциальные уравнения ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ В ЧАСТНЫХ ПРОИЗВОДНЫХ искомая функция зависит от одной переменной искомая функция
- 4. Дифференциальные уравнения ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ n-ОГО ПОРЯДКА F – некоторая функция от n+2 переменных, x
- 5. Дифференциальные уравнения Определение Решением дифференциального уравнения (1) называется функция y(x), имеющая производные до n-ого порядка включительно,
- 6. Дифференциальные уравнения ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ Общее решение дифференциального уравнения зависит от произвольных постоянных,
- 7. Дифференциальные уравнения Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения График
- 8. Пример Из статистических данных известно, что для некоторого региона число новорожденных и число умерших за единицу
- 9. Решение Пусть y=y(t) – число жителей региона в момент времени t. Число родившихся в момент времени
- 10. Решение Переходя к пределу при , получим уравнение Решим это уравнение: C – постоянная, определяемая начальным
- 11. Дифференциальные уравнения Определение Отыскание частного решения дифференциального уравнения (1) n-ого порядка, удовлетворяющего n начальным условиям вида:
- 12. Дифференциальные уравнения 1 порядка ОБЩИЙ ВИД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 1-ОГО ПОРЯДКА (2) ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ОГО ПОРЯДКА, РАЗРЕШЕННОЕ
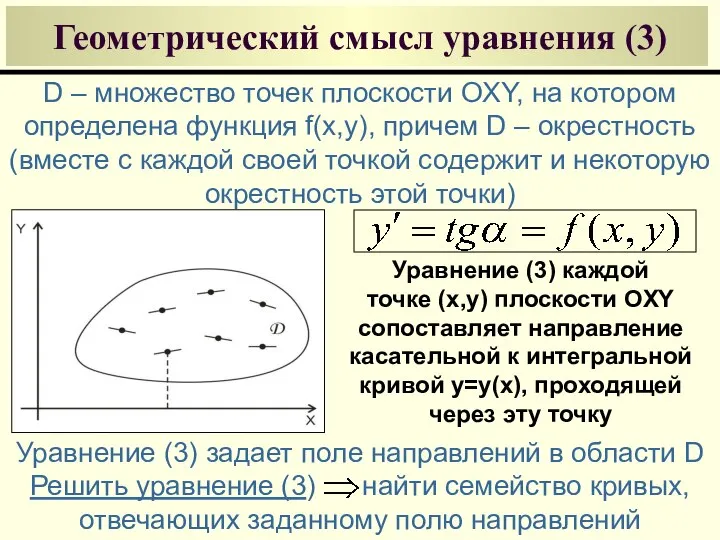
- 13. Геометрический смысл уравнения (3) D – множество точек плоскости OXY, на котором определена функция f(x,y), причем
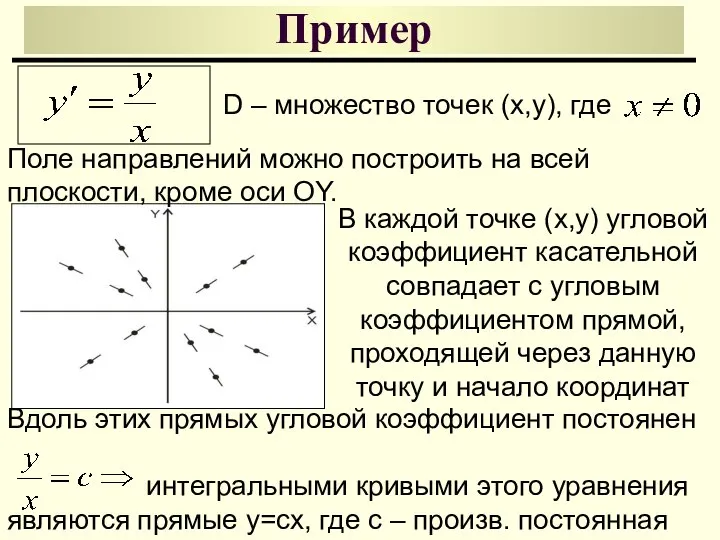
- 14. Пример D – множество точек (x,y), где В каждой точке (x,y) угловой коэффициент касательной совпадает с
- 15. Дифференциальные уравнения ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИМЕЕТ БЕСКОНЕЧНОЕ МНОЖЕСТВО РЕШЕНИЙ Задача о нахождении решений дифференциального уравнения (3), удовлетворяющих
- 16. Дифференциальные уравнения Теорема Если в уравнении функция f(x,y) и ее частная производная непрерывны в некоторой области
- 18. Скачать презентацию













 Чтобы найти целое, нужно сложить части
Чтобы найти целое, нужно сложить части Тригонометрические уравнения. Найди пару
Тригонометрические уравнения. Найди пару Новогодние приключения Маши и Вити. Вычислялки
Новогодние приключения Маши и Вити. Вычислялки Оценки параметров распределения
Оценки параметров распределения Презентация на тему Цифра 5, число 5, состав числа 5
Презентация на тему Цифра 5, число 5, состав числа 5  قدرمطلقی درجه اول
قدرمطلقی درجه اول Презентация на тему Знакомые и незнакомые единицы измерения площади
Презентация на тему Знакомые и незнакомые единицы измерения площади  Экзаменационные задания по теме вычисления (степени и корни)
Экзаменационные задания по теме вычисления (степени и корни)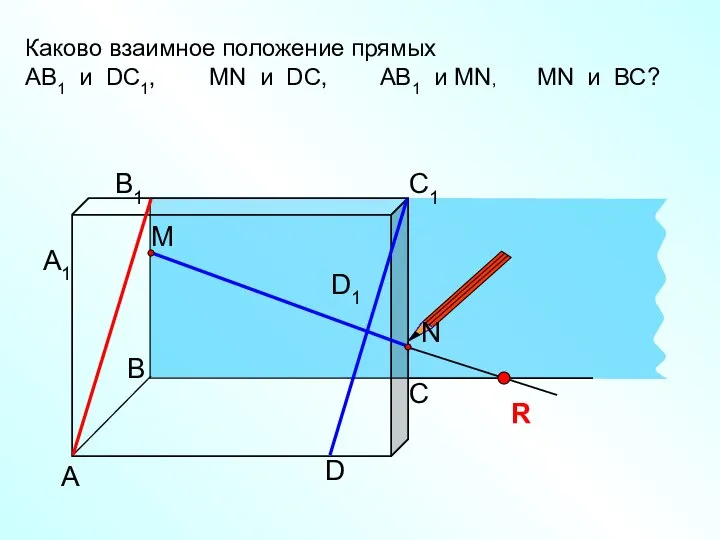 параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10 Объём. Начало геометрии
Объём. Начало геометрии Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Решение задач
Решение задач Исследование функции с помощью производной
Исследование функции с помощью производной Вписанная и описанная окружность
Вписанная и описанная окружность Аксиомы планиметрии (часть 1)
Аксиомы планиметрии (часть 1) Сокращение дробей
Сокращение дробей Сложная функция. Производная сложной функции
Сложная функция. Производная сложной функции Движение: скорость, время, расстояние
Движение: скорость, время, расстояние Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Центральная симметрия
Центральная симметрия Презентация на тему Геометрические фигуры и объекты
Презентация на тему Геометрические фигуры и объекты  Решение задач на проценты. Повторение, обобщение
Решение задач на проценты. Повторение, обобщение Математика.Управление социальными системами. Математический анализ. Функции. Пределы. Непрерывность
Математика.Управление социальными системами. Математический анализ. Функции. Пределы. Непрерывность Домашнее задание к занятию №3. 5 класс
Домашнее задание к занятию №3. 5 класс Презентация на тему Осевая и центральная симметрия (8 класс)
Презентация на тему Осевая и центральная симметрия (8 класс)  Презентация на тему Виды многогранников
Презентация на тему Виды многогранников