Слайд 2 Обучение школьников метапредметным знаниям требует консолидированного участия учителей математики и учителей-

предметников.
Сущность использования метода обучения состоит в варьировании сюжета, условий и предметного содержания задач, при сохранении ключевого понятия, заложенного в основу эвристического приема их решения.
Слайд 3КЛЮЧЕВЫЕ СЛОВА:
Развивающее обучение, метапредметные знания,
общенаучные понятия,
интеграция естественно-

научного и математического образования школьников.
Слайд 41.Химический профиль: задача о скорости химической реакции
Пусть некоторое вещество вступает в химическую

реакцию. Количество этого вещества, вступившее уже в реакцию к моменту времени t, обозначим через y(t). Таким образом, y есть функция времени, то за промежуток времени от момента t до момента t+Δt вступит в реакцию ещё некоторое количество вещества Δy=y(t+Δt)- y(t). Следовательно, отношение Δy/Δt выразит среднюю скорость химической реакции за промежуток времени Δt. Для характеристики скорости химической реакции в данный момент t следует рассмотреть предел этого отношения при Δt →0.
Слайд 52.Физический профиль: задача о мгновенной величине тока
Представим себе электрическую цепь с некоторым

источником тока. Обозначим через q=q(t) количество электричества (в кулонах), протекающее через поперечное сечение проводника за время t. Количество электричества есть функция времени, так как каждому значению времени t соответствует определённое значение количества электричества. Пусть Δt – некоторый промежуток времени, Δq=q(t+Δt)-q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента времени t до момента t+Δt. Тогда отношение Δq/Δt называют средней силой тока за промежуток времени Δt и обозначают Iср. Иначе говоря, средней силой тока называется количество электричества, протекающее по проводнику в единицу времени. В случае постоянного тока Iср будет постоянной. Если в цепи переменный ток, то Iср будет различна для различных промежутков времени. Поэтому для цепи переменного тока вводят понятие мгновенной силы тока, или силы тока в данный момент времени t.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, за которое произошло это приращение, при условии, что Δt → 0.
Слайд 63.Биологический профиль: задача о скорости роста популяции
Пусть p=p(t) – размер популяции

бактерий в момент t. Таким образом, p есть функция времени. За промежуток времени от момента t до момента t+Δt размер популяции бактерий изменится на некоторое значение Δp=p(t+Δt)- p(t). Следовательно, отношение Δp/Δt выразит среднюю скорость изменения численности бактерий в популяции. Для характеристики скорости изменения численности бактерий в популяции в данный момент t следует рассмотреть предел этого отношения при Δt → 0.
Слайд 74.Гуманитарный профиль: задача о скорости чтения текста.
Представим себе человека, читающего некий

текст. Обозначим через y=y(t) количество букв, прочитываемое им за время t. Количество букв y есть функция времени, так как каждому значению времени t соответствует определённое значение количества букв. Пусть Δt – некоторый промежуток времени, Δy=y(t+Δt)-y(t) – количество букв, прочитанное человеком за промежуток времени от момента времени t до момента t+Δt. Тогда отношение Δy/Δt называют средней скоростью чтения за промежуток времени Δt. Чтобы узнать скорость чтения текста в момент времени t, следует рассмотреть предел отношения Δy/Δt, при условии, что Δt → 0.
Слайд 85. Экономический профиль: задача о предельных издержках производства
Издержки производства y будем

рассматривать как функцию количества выпускаемой продукции x. Пусть Δt – прирост продукции, тогда Δy – приращение издержек производства. Отношение Δy/Δx выражает среднее приращение издержек производства на единицу продукции. Предел отношения Δy/Δx, при условии, что Δt → 0, покажет предельные издержки производства и будет характеризовать приближённо дополнительные затраты на производство единицы дополнительной продукции.







 Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄ Решение задач 11 класс
Правила дифференцирования (f(x)+g(x))΄ и (c f(x))΄ Решение задач 11 класс Презентация на тему Понятие движения
Презентация на тему Понятие движения  Решение задач на межпредметные связи
Решение задач на межпредметные связи Множество. Элемент множества
Множество. Элемент множества Площадь трапеции
Площадь трапеции Тригонометрия. Сумма и разность синуса, косинуса
Тригонометрия. Сумма и разность синуса, косинуса Презентация на тему Деление и дроби (5 класс)
Презентация на тему Деление и дроби (5 класс)  Конструирование из геометрических фигур
Конструирование из геометрических фигур Математическое моделирование. Контурно-графический анализ
Математическое моделирование. Контурно-графический анализ Кенгуру – математика для всех
Кенгуру – математика для всех Теория вероятности в жизни пчел
Теория вероятности в жизни пчел Неравенства и их системы
Неравенства и их системы Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Сравнение натуральных чисел
Сравнение натуральных чисел Задачи на проценты
Задачи на проценты Цифры в буквах
Цифры в буквах Математические станции
Математические станции Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Симметрия. Симметричные объекты. Платоновы тела
Симметрия. Симметричные объекты. Платоновы тела Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аксиомы стереометрии
Аксиомы стереометрии Тригонометрические функции
Тригонометрические функции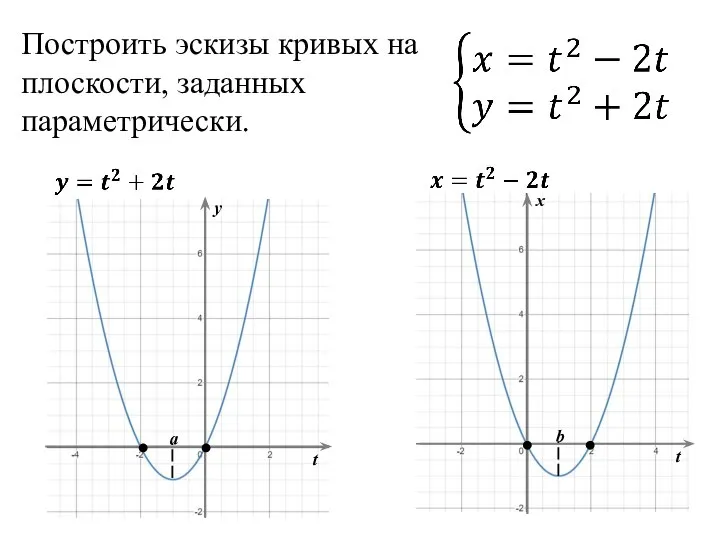 Построить эскизы кривых на плоскости, заданных параметрически
Построить эскизы кривых на плоскости, заданных параметрически Свойства логарифмов
Свойства логарифмов Информационные технологии образовании
Информационные технологии образовании Прямая. Ортогональные проекции прямой линии
Прямая. Ортогональные проекции прямой линии