Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)

1. Понятие статистического моделирования случайных процессов.
2. Статистическое моделирование случайных величин.
Учебные вопросы

Литература
1.Асанин А.В., Войцеховский В.Ф. Основы теории оптимальной фильтрации: Учебное пособие. Химки. АГЗ, 2020.
2.Войцеховский В.Ф., Григорьева Е.Д. Основы теории оптимальной фильтрации: Учебное пособие. Химки. АГЗ, 2017.
3.Войцеховский В.Ф. Основы статистической теории радиоэлектронных систем: Учебное пособие. Химки. АГЗ, 2013.
1

1-ый учебный вопрос
«Понятие статистического моделирования случайных процессов»

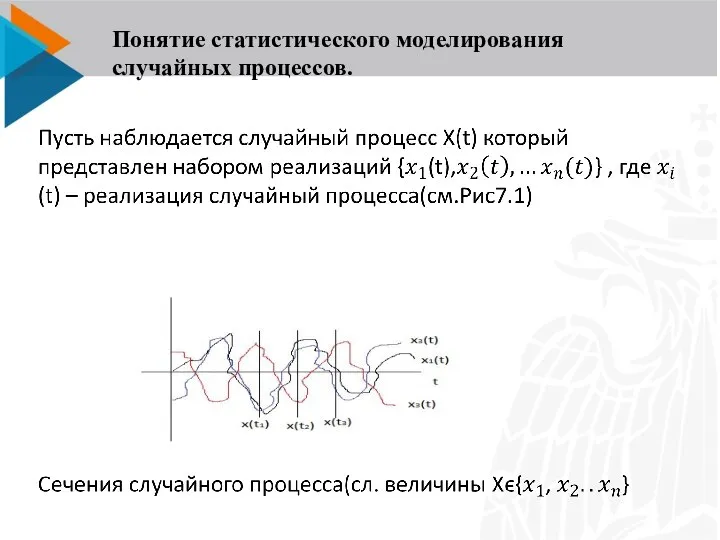
Понятие статистического моделирования случайных процессов.

Сечение случайного процесса представляет собой случайную величину появляющуюся с определенной вероятностью, т.е. мы можем представить случайную величину в виде определенных этапов ( сечений СП). Моделирование случайного процесса X(t) можно осуществить методом моделирования случайных величинах на каждом этапе. Совокупность дает нам модель реализации случайного процесса.

2-ой учебный вопрос
«Статистическое моделирование случайных величин»

Статистическое моделирование случайных величин
Так как сечения случайного процесса представляют собой случайные величины то очевидно моделирование каждого этапа, это моделирование случайной величины. В качестве инструмента моделирования используют генераторы (датчики) случайных чисел.
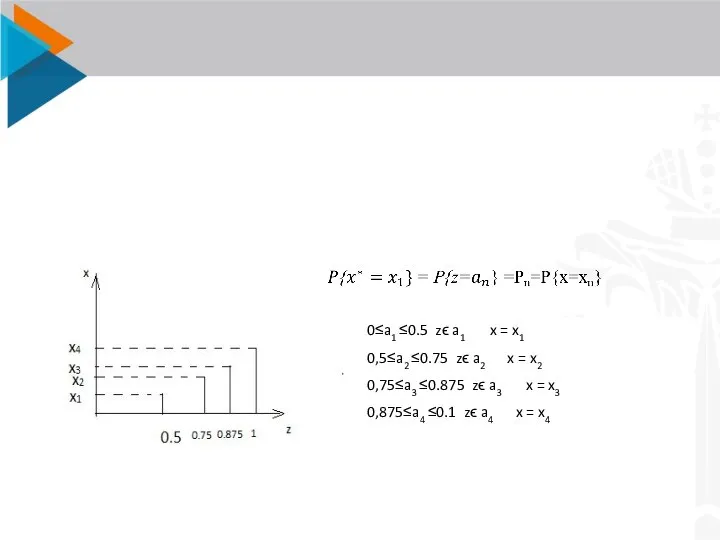
Рассмотрим пример розыгрыша случайной величины, которая задана рядом вероятностей. (см.Табл1)

Можно использовать круг , где соответствующая площадь соответствует определенной части от общей площади. На основе этого датчика случайных чисел, можно получить, распределение дискретных случайных величин распределенных по заданному закону. В данном примеры рассмотрен простейший способ розыгрыша случайной величины .

0≤a1 ≤0.5 zϵ a1 x = x1
0,5≤a2 ≤0.75 zϵ a2 x = x2
0,75≤a3 ≤0.875 zϵ a3 x = x3
0,875≤a4 ≤0.1 zϵ a4 x = x4

Моделирование непрерывной СВ .
(преобразование равномерного закона распределения в заданный)
Дано: X – непрерывная СВ с известным законом распределения.
Требуется разыграть эту случайную величину X с заданным законом распределения,p(х) на основе преобразование случайных чисел Z, распределенных равномерно, на интервале от 0 до 1.
Рис 2 Плотность вероятностей случайной величины z .

Равномерный закон для Х и Z.

Пример