Примеры использования OpenMP. Вычисление определенного интеграла

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Метод прямоугольников

Последовательность выполнения
Последовательная версия.
Базовая реализация алгоритма интегрирования
Эффект применения компилятора
Использование предварительных вычислений сложных функций
Алгоритмическая оптимизация
Параллельная версия.
Варианты распараллеливание базового алгоритма
Распараллеливание оптимизированного алгоритма

Базовый алгоритм
Должен содержать код, несколько раз запускающий тестируемую реализацию алгоритма вычислений.
Должен вычислять минимальное, максимальное и среднее времена ее работы.
Должен представлять результаты вычислений.
Параметры вычислений задаются в программе.
Провести анализ использования разных режимов компиляции.

Распараллеливание базового алгоритма
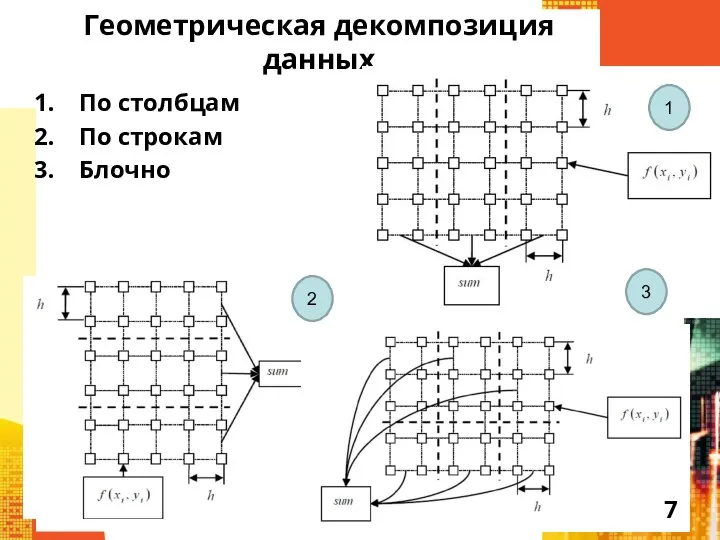
Геометрическая декомпозиция данных (разделение данных на части и применение к ним одного и того же алгоритма).
Локализация данных.
Анализ результатов (гонка данных).

Геометрическая декомпозиция данных
По столбцам
По строкам
Блочно
1
2
3

Оптимизация базового алгоритма
Предварительное вычисление сложных математических функций (sin, cos, exp и др.).
Алгоритмическая оптимизация (исключение многократного вычисления одних и тех же данных, предварительные расчеты).
Буферизация.

Распараллеливание оптимизированного алгоритма
Распараллеливание с учетом уже полученных результатов:
В данной задаче наилучшие результаты дает распараллеливание с разделением сетки интегрирования по столбцам (внешний цикл).
Распараллелить основные вычислительные циклы.

Пример выполнения вычислений

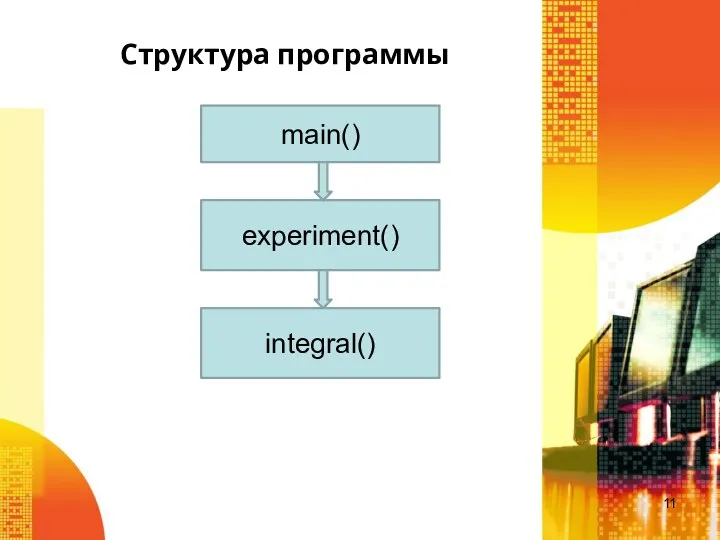
Структура программы
main()
experiment()
integral()

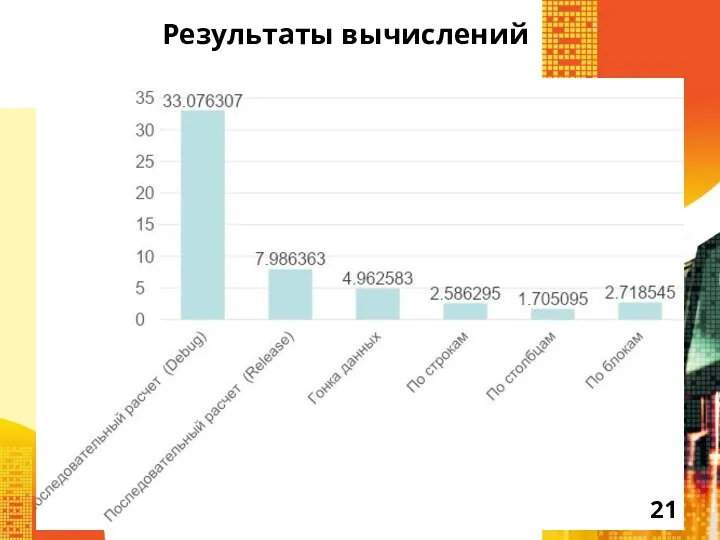
Пример выполнения вычислений
Базовый алгоритм

Основная программа
int main () {
int i;
double time, res, min_time, max_time, avg_time;
int numbExp = 10;
min_time = max_time = avg_time = experiment(&res);
for(i = 0; i < numbExp - 1; i ++) {
time = experiment(&res);
avg_time += time;
if(max_time < time) max_time = time;
if(min_time > time) min_time = time; }
printf(“Интеграл равен: %lf; \n", res);
printf(«Время выполнения: %lf; %lf; %lf \n",
avg_time / numbExp, min_time, max_time);
return 0;
}

Функция experiment
double experiment(double *res)
{
double stime, ftime;
double a1 = 0.0 ;
double a1 = a2 = 0.0 ;
double b1 = 16.0;
double b2 = 16.0;
double h = 0.001;
stime = omp_get_wtime( );
integral(a1, b1, a2, b2, h, res);
ftime = omp_get_wtime( );
return (ftime - stime);
}

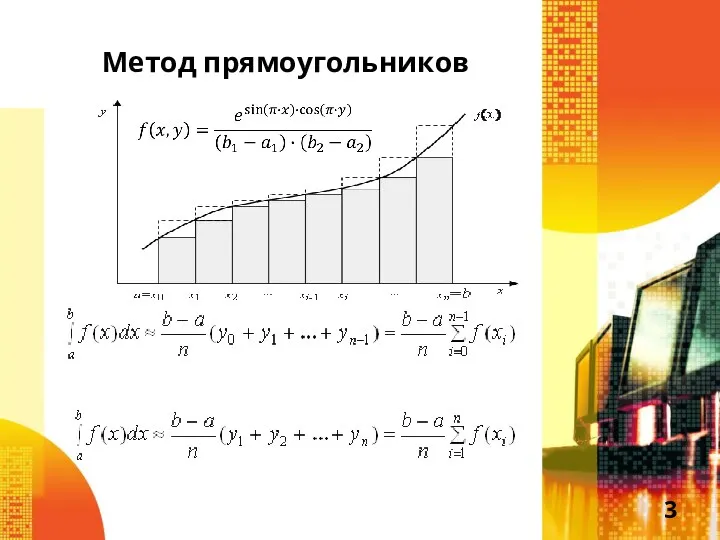
Функция integral
void integral(const double a1, const double b1,
const double a2, const double b2, const double h,
double *res){
int i, j, n1, n2; double sum, x, y;
n1 = (int)((b1 - a1) / h); n2 = (int)((b2 - a2) / h);
sum = 0.0;
for( i = 0; i < n1; i++) {
for(j = 0; j < n2; j++) {
x = a1 + i * h + h / 2;
y = a2 + j * h + h / 2;
sum += ((exp(sin(x * PI) * cos(y * PI)) + 1) / ((b1 - a1) * (b2 - a2))) * h * h; } }
*res = sum;
}

Пример выполнения вычислений
Базовый алгоритм - распараллеливание

Распараллеливание по столбцам
#pragma omp parallel for
for(i = 0; i < n1; i++)
{
for(j = 0; j < n2; j++)
{
x = a1 + i * h + h / 2;
y = a2 + j * h + h / 2;
sum += ((exp(sin(x * PI) * cos(y * PI)) + 1) / ((b1 - a1) *
(b2 - a2))) * h * h;
}
}

Распараллеливание по столбцам с учетом data race
#pragma omp parallel for private (x, y, j)
reduction(+: sum)
for(i = 0; i < n1; i++)
{
for(j = 0; j < n2; j++)
{
x = a1 + i * h + h / 2;
y = a2 + j * h + h / 2;
sum += ((exp(sin(x * PI) * cos(y * PI)) + 1) / ((b1 - a1) *
(b2 - a2))) * h * h;
}
}

Распараллеливание по строкам
for(i = 0; i < n1; i++)
{
#pragma omp parallel for private (x, y)
reduction(+: sum)
for(j = 0; j < n2; j++)
{
x = a1 + i * h + h / 2;
y = a2 + j * h + h / 2;
sum += ((exp(sin(x * PI) * cos(y * PI)) + 1) / ((b1 - a1) *
(b2 - a2))) * h * h;
}
}

Блочное разделение данных
omp_set_nested(true);
#pragma omp parallel for
for (i = 0; i < n1; i++)
{
#pragma omp parallel for private (x, y)
reduction(+: sum)
for(j = 0; j < n2; j++)
{
x = a1 + i * h + h / 2;
y = a2 + j * h + h / 2;
sum += ((exp(sin(x * PI) * cos(y * PI)) + 1) /
((b1 - a1) * (b2 - a2))) * h * h;
}
}

Результаты вычислений

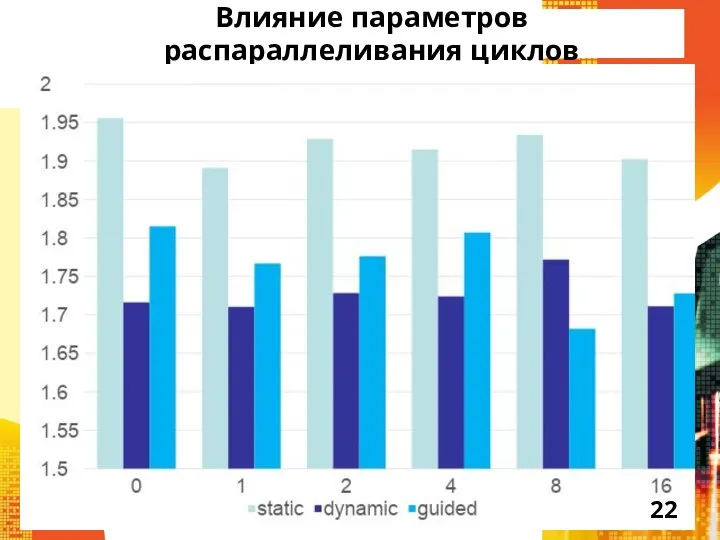
Влияние параметров распараллеливания циклов

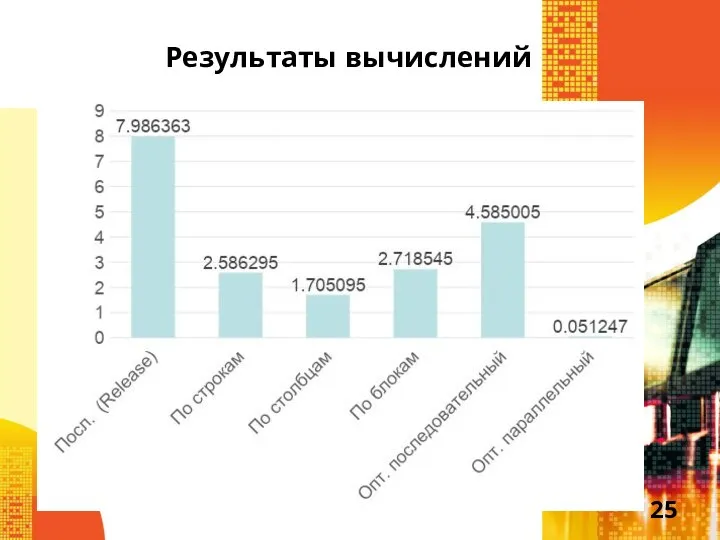
Пример выполнения вычислений
Оптимизированный алгоритм –
распараллеливание

Использование предварительных вычислений сложных функций
void integral(const double a1, const double b1,
const double a2, const double b2, const double h, double *res) { int i, j, n1, n2; double sum, x, y, *sinx, *cosy; n1 = (int)((b1 - a1) / h);
n2 = (int)((b2 - a2) / h); sum = 0.0;
sinx = new double [n1]; cosy = new double [n2];
for(i = 0; i < n1; i++)
{ x = a1 + i * h + h / 2; sinx[i] = sin(x * PI); }
for(j = 0; j < n2; j++)
{ y = a2 + j * h + h / 2; cosy[j] = cos(y * PI); }
for(i = 0; i < n1; i++)
{ for(j = 0; j < n2; j++) {sum += ((exp(sinx[i] * cosy[j]) + 1) / ((b1 - a1) * (b2 - a2))) * h * h; } } *res = sum;
delete [] sinx; delete [] cosy; }

Результаты вычислений

Загрузка ядер процессора
Последовательный алгоритм
Оптимизированный параллельный алгоритм
Параллельный алгоритм

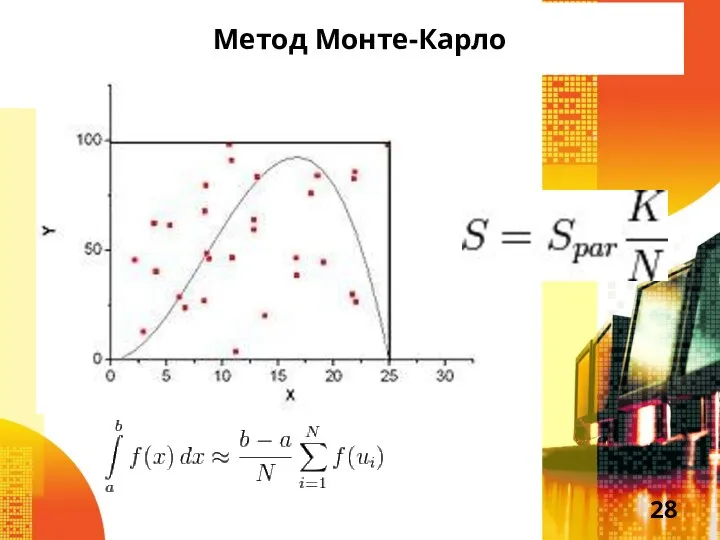
Пример выполнения вычислений
Вычисление интеграла методом Монте-Карло

Метод Монте-Карло

Функция integral
void integral(const double a1, const double b1, const double a2, const double b2, const double h, double *res) {
int n=0; double sum, x, y, f;
for(long int i=1;i<= nMax;i++) { x=abs((double)(rand()%((int)(b1 - a1)*Mrand))) /Mrand;
y=abs((double)(rand()% ((int)(b2 - a2)*Mrand)))/Mrand;
f=abs((double)(rand()% ((int)(Fmax*Mrand))))/Mrand;
if(func(x+a1, y+a2, a1, b1, a2, b2) <= f) n++; }
sum=(b1 - a1)*(b2 - a2)*(Fmax)*n/nMax;
*res = sum;
}