Геометрия. Что значит это слово? часть 1

Планиметрия
«плано»
плоскость
Из каких разделов состоит геометрия?
Стереометрия
«Stereos»
Телесный,
объемный, пространственный
?
?

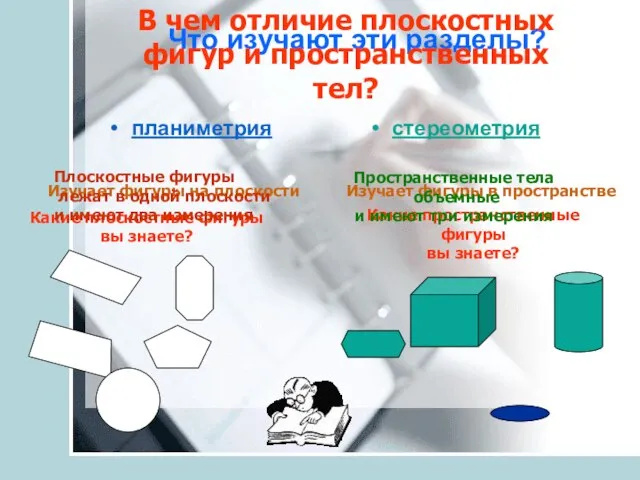
Что изучают эти разделы?
планиметрия
стереометрия
Изучает фигуры на плоскости
Изучает фигуры в пространстве
Какие плоскостные фигуры
вы знаете?
Какие пространственные фигуры
вы знаете?
В чем отличие плоскостных фигур и пространственных тел?
Плоскостные фигуры
лежат в одной плоскости
и имеют два измерения
Пространственные тела
объемные
и имеют три измерения

Машиностроении

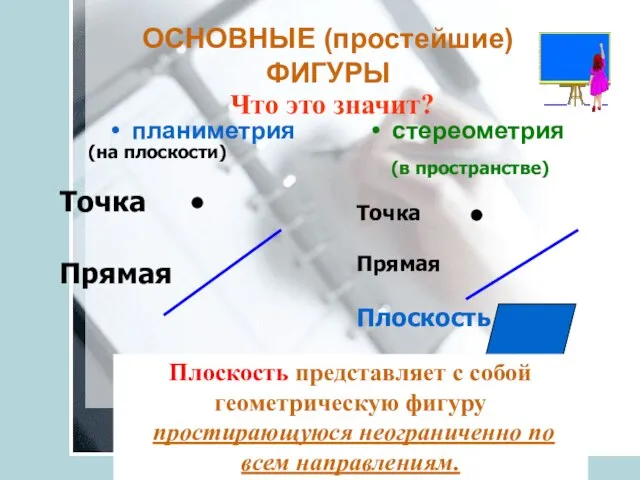
ОСНОВНЫЕ (простейшие) ФИГУРЫ
планиметрия
стереометрия
(на плоскости)
Точка
Прямая
(в пространстве)
Точка
Прямая
Плоскость
Плоскость представляет с собой геометрическую фигуру
простирающуюся неограниченно по всем направлениям.
Что это значит?

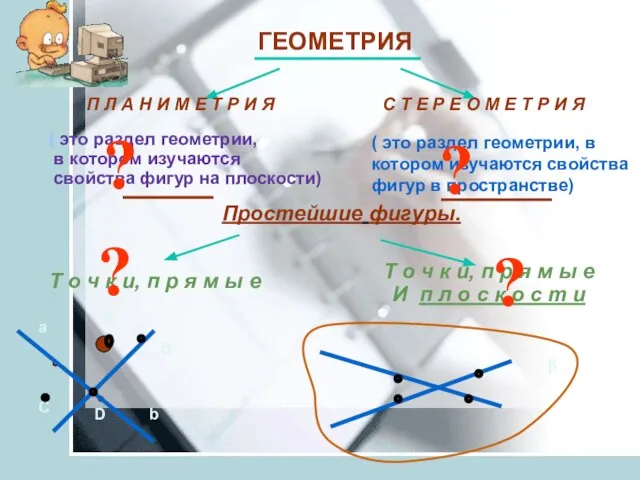
ГЕОМЕТРИЯ
П Л А Н И М Е Т Р И Я
С Т Е Р Е О М Е Т Р И Я
( это раздел геометрии,
в котором изучаются
свойства фигур на плоскости)
( это раздел геометрии, в котором изучаются свойства фигур в пространстве)
Простейшие фигуры.
Т о ч к и, п р я м ы е
А
В
С
D
a
b
Т о ч к и, п р я м ы е
И п л о с к о с т и
β
?
?
?
?

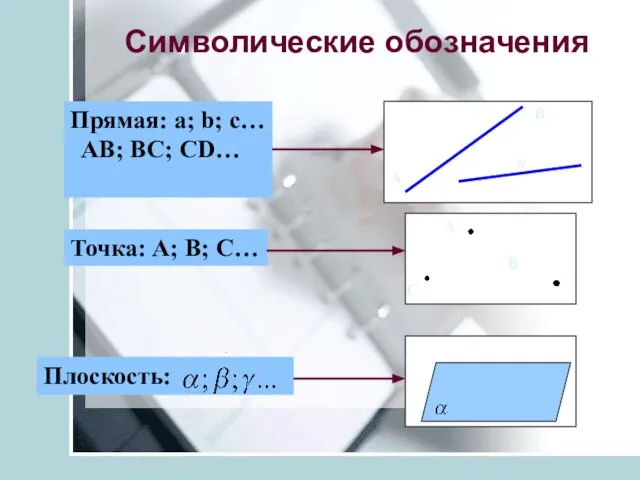
Символические обозначения
Точка: A; B; C…
Прямая: a; b; c…
AB; BC; CD…
Плоскость:
C
A
B

Обозначения
Принадлежит, лежит
Не принадлежит, не лежит
пересекается
содержится

П р о ч т и ч е р т е ж
С
А

П р о ч т и ч е р т е ж
b
c
B
С

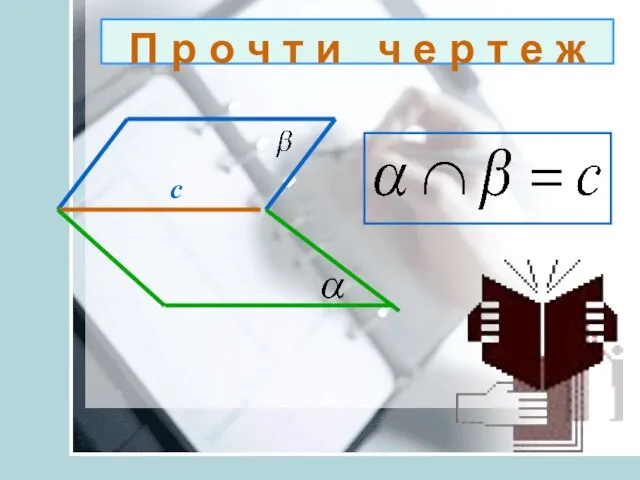
П р о ч т и ч е р т е ж
с

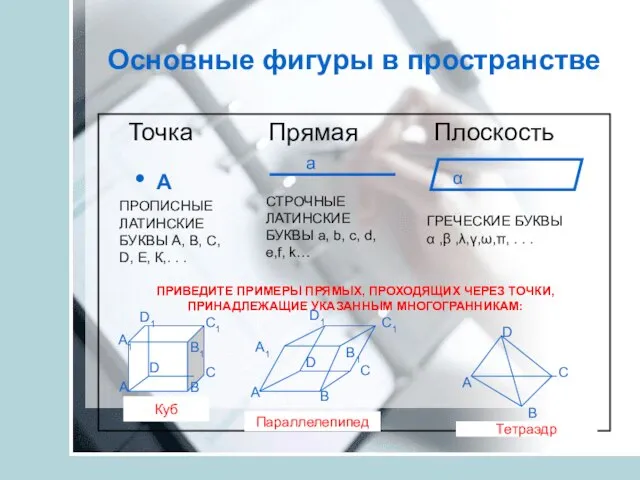
Основные фигуры в пространстве
Точка Прямая Плоскость
• А
a
α
ПРОПИСНЫЕ ЛАТИНСКИЕ БУКВЫ А, В, С, D, Е, К,. . .
СТРОЧНЫЕ ЛАТИНСКИЕ БУКВЫ a, b, c, d, e,f, k…
ГРЕЧЕСКИЕ БУКВЫ α ,β ,λ,γ,ω,π, . . .
ПРИВЕДИТЕ ПРИМЕРЫ ПРЯМЫХ, ПРОХОДЯЩИХ ЧЕРЕЗ ТОЧКИ, ПРИНАДЛЕЖАЩИЕ УКАЗАННЫМ МНОГОГРАННИКАМ:
А
В
С
С1
D1
А
В
С
D
D
А1
А
В
С
А1
С1
D1
D
В1
В1
Куб
Параллелепипед
Тетраэдр

А к с и о м а
(от греч. “a x i ό m a” принимаемое без доказательства)
Исходное положение
научной теории
принимаемое без
доказательства

некоторые
Аксиомы планиметрии
Какова бы ни была прямая.
Существуют точки,
Принадлежащие этой прямой,
и точки, не принадлежащие ей
Через любые две точки
можно провести прямую
и только одну
Из трех точек прямой
Одна и только одна
Лежит между двумя
другими
Каждый отрезок имеет
Определенную длину,
большую нуля
Длина отрезка равна
Сумме длин частей,
на которые он разбивается
Любой его точкой
Прямая, принадлежащая плоскости,
Разбивает эту плоскость
На две полуплоскости

Аксиома
С
А
Какова бы ни была плоскость,
существуют точки,
принадлежащие этой плоскости,
и точки, не принадлежащие ей

А1. Через любые три точки,
не лежащие на одной прямой,
проходит плоскость,
и притом только одна
A
B
C

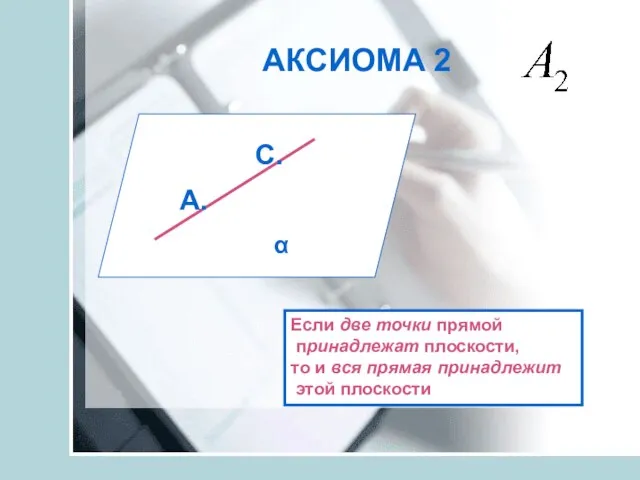
АКСИОМА 2
А.
С.
α
Если две точки прямой
принадлежат плоскости,
то и вся прямая принадлежит
этой плоскости

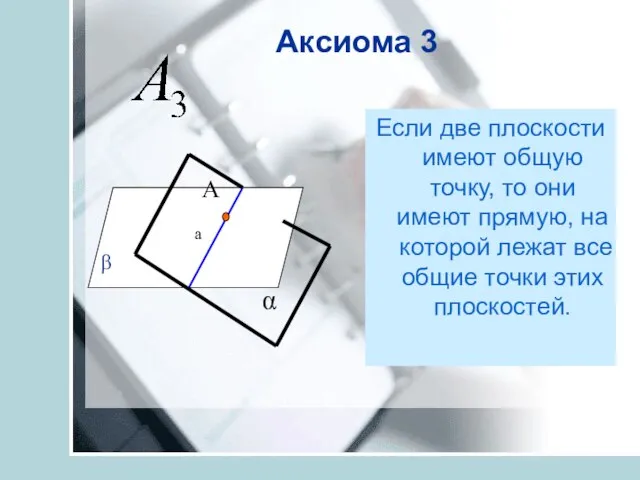
Аксиома 3
Если две плоскости имеют общую точку, то они имеют прямую, на которой лежат все общие точки этих плоскостей.

Точка, лежащая на линии пересечения двух плоскостей, лежит на каждой из этих плоскостей
Точка, лежащая на двух каких-нибудь плоскостях, лежит на линии пересечения этих плоскостей

Аксиомы стереометрии
Сформулируйте аксиомы А1, А2, А3.
Прокомментируйте их с помощью приведенных рисунков.
А, В,С – произвольные точки,
не лежащие на одной прямой.
Через точки А, В, С проходит
единственная плоскость α.

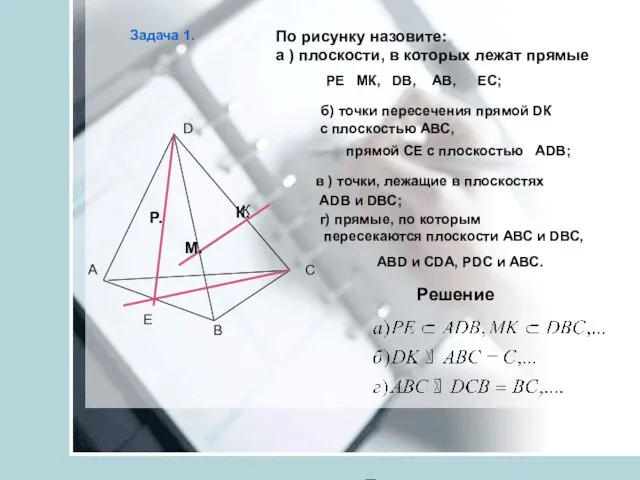
А
В
С
D
Е
К
К.
М.
Р.
Решение
Задача 1.
По рисунку назовите:
a ) плоскости, в которых лежат прямые
РЕ
МК,
DВ,
АВ,
ЕС;
б) точки пересечения прямой DК
с плоскостью АВС,
прямой СЕ с плоскостью АDВ;
в ) точки, лежащие в плоскостях
АDВ и DВС;
г) прямые, по которым
пересекаются плоскости АВС и DВС,
АВD и СDА, РDС и АВС.