Назначение и описание критерия Фишера

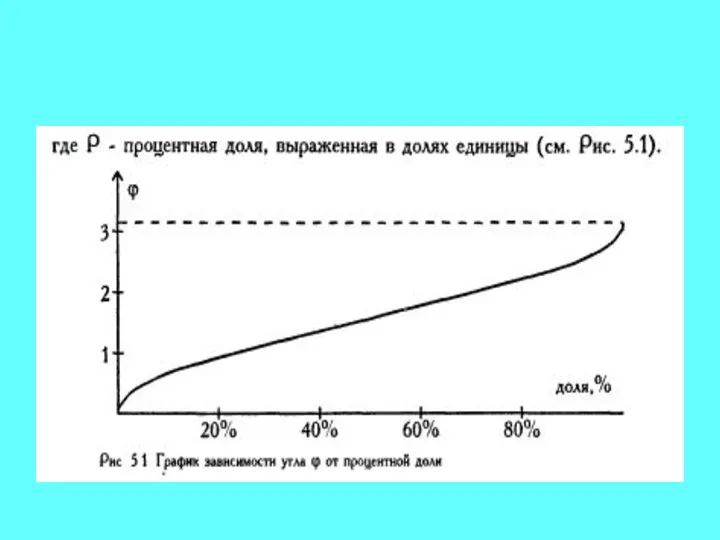
Большей процентной доле будет соответствовать больший угол φ, а меньшей доле - меньший угол, но соотношения здесь не линейные: φ = 2*arcsin(√Р), где P - процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.

Графическое представление критерия
Метод углового преобразования несколько более абстрактен, чем остальные критерии.
Формула, которой придерживается Е.В. Гублер при подсчете критерий φ*,предполагает , что 100% составляют угол φ=3,142 , т.е. округленную величину Пи= 3,14159… Это позволяет нам представить сопоставляемые выборки в виде двух полукругов. Каждый из которых символизирует 100% численности своей выборки. Процентные доли испытуемых с «Эффектом» будут представлены как секторы, образованные разными углами φ

Ограничения критерия Фишера
1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным (Гублер Е.В., 1978, с. 86).
2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими.

Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:
а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30: n1=2 -> n2≥30;
б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7: n1=3 -> n2≥7;
в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5: n1=4 -> n2≥5;
г) при n1, n2≥5 возможны любые сопоставления.

Гипотезы критерия Фишера
H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.

Допустим, нас интересует, различаются ли две группы студентов по успешности решения новой экспериментальной задачи. В первой группе из 20 человек с нею справились 12 человек, а во второй выбор­ке из 25 человек - 10. В первом случае процентная доля решивших за­дачу составит 12/20·100%=60%, а во второй 10/25·100%=40%. Дос­товерно ли различаются эти процентные доли при данных n1 и n2?
Казалось бы, и "на глаз" можно определить, что 60% значительно выше 40%. Однако на самом деле эти различия при данных n1, n2 недостоверны.
Проверим это. Поскольку нас интересует факт решения задачи, будем считать "эффектом" успех в решении экспериментальной задачи, а отсутствием эффекта - неудачу в ее решении.

Сформулируем гипотезы.
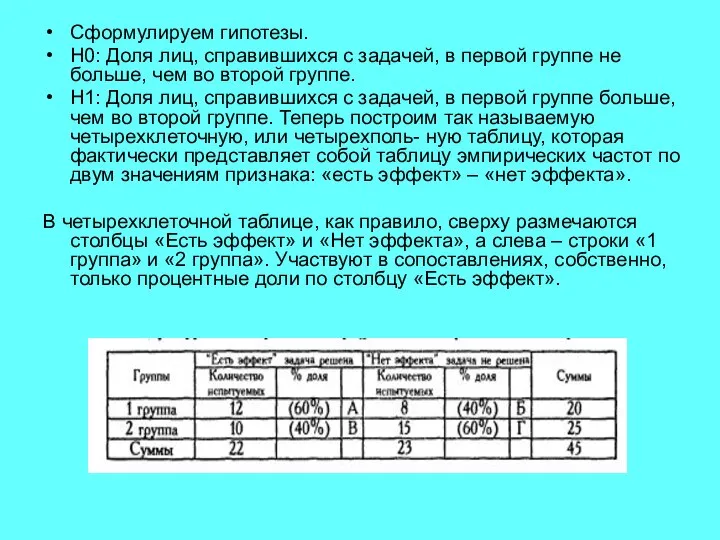
H0: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.
Н1: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе. Теперь построим так называемую четырехклеточную, или четырехполь- ную таблицу, которая фактически представляет собой таблицу эмпирических частот по двум значениям признака: «есть эффект» – «нет эффекта».
В четырехклеточной таблице, как правило, сверху размечаются столбцы «Есть эффект» и «Нет эффекта», а слева – строки «1 группа» и «2 группа». Участвуют в сопоставлениях, собственно, только процентные доли по столбцу «Есть эффект».