Слайд 2Теория вероятностей.
Определения:
Событием называется всякий факт, который может произойти или не произойти

в результате опыта;
События называются несовместными, если появление одного из них исключает появление других. Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте);
Слайд 3Полной группой событий называется совокупность всех возможных результатов опыта;
Достоверным событием называется событие,

которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Слайд 4Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется

невозможным, если оно никогда не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Слайд 5Вероятностью события А называется математическая оценка возможности появления этого события в результате

опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.
Слайд 6Пример. В коробке находится 10 шаров. 3 из них красные, 2 –

зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара - событие А, появление зеленого - событие В, появление белого –С.
Тогда в соответствием с записанными выше формулами получаем:
Слайд 7Относительной частотой события А называется отношение числа опытов, в результате которых произошло

событие А к общему числу опытов.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:
Слайд 8Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих

событий
P(A+B)=P(A)+P(B)
Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Слайд 9Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна

произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Если события независимые, то, и теорема умножения вероятностей принимает вид:
P(AB)=P(A)P(B).
Слайд 10Если в результате испытания может появиться п событий, независимых в совокупности, то

вероятность появления хотя бы одного из них равна
Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?
Вероятность выпадения 6 очков при одном броске кости равна 1/6.Вероятность того, что не выпадет 6 очков – 5/6. Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна 1-125/216=91/216/









 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Тест. Равенство треугольников
Тест. Равенство треугольников Логарифм числа
Логарифм числа Презентация по математике "Сложение и вычитание в пределах 1000" -
Презентация по математике "Сложение и вычитание в пределах 1000" -  Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сложение с числом 10
Сложение с числом 10 Линейная корреляция
Линейная корреляция Проецирование – это процесс получения
Проецирование – это процесс получения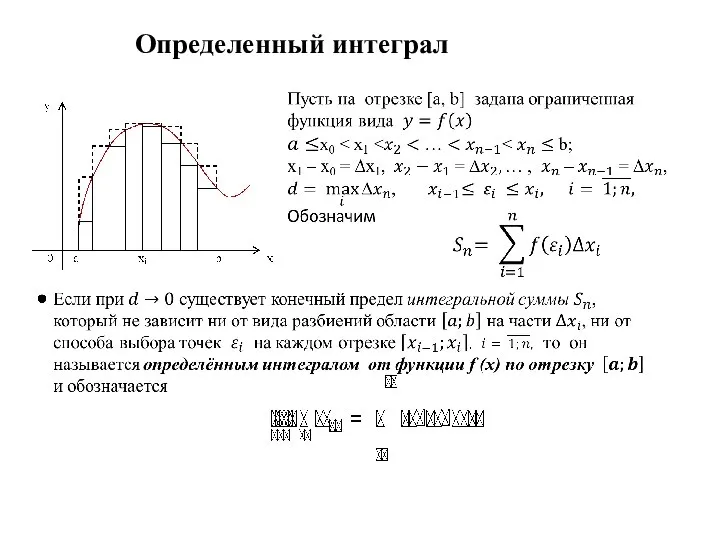 Определённый интеграл
Определённый интеграл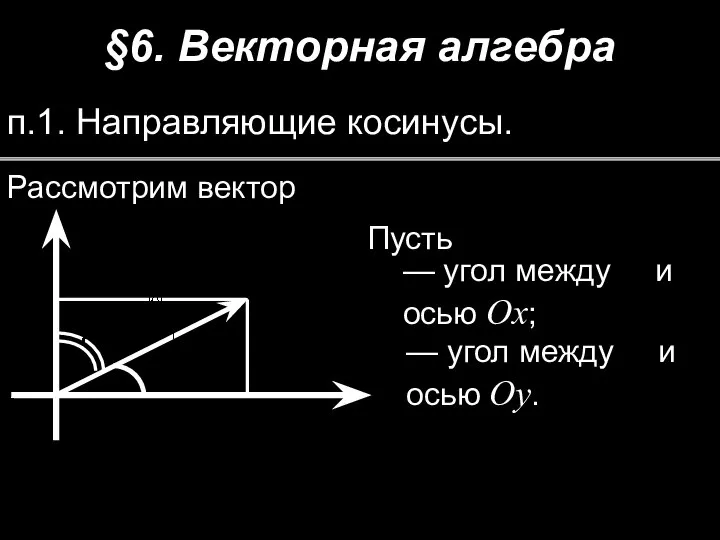 2.3. Векторная алгебра
2.3. Векторная алгебра Признаки параллельности прямых
Признаки параллельности прямых Решение задач. Урок математики
Решение задач. Урок математики Сложение вида + 1, вычитание вида -1
Сложение вида + 1, вычитание вида -1 Подготовка к ЕГЭ
Подготовка к ЕГЭ Цифры - прописи. Анимированный плакат
Цифры - прописи. Анимированный плакат Лекция 5. Трехмерные преобразования
Лекция 5. Трехмерные преобразования Кратные чисел. 5 класс
Кратные чисел. 5 класс 2020.09.03 Десятичная система записи натуральных чисел
2020.09.03 Десятичная система записи натуральных чисел Pervoobraznaya
Pervoobraznaya Итоговой тест по геометрии. 9 класс
Итоговой тест по геометрии. 9 класс Приведение уравнений фигур к каноническому виду при помощи квадратичных форм
Приведение уравнений фигур к каноническому виду при помощи квадратичных форм Решение треугольников
Решение треугольников Треугольник. Виды треугольников
Треугольник. Виды треугольников Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов Сплайн интерполяция. Отчёт по домашней работе №3
Сплайн интерполяция. Отчёт по домашней работе №3 Иррациональные числа
Иррациональные числа Тест 3 по математике
Тест 3 по математике