Содержание
- 2. Результат теста Верно: 14 Ошибки: 0 Отметка: 5 Время: 1 мин. 51 сек. ещё
- 3. Вариант 1 а) V=S∙ℓ∙sin? в) V=S∙ℓ∙tg? 1. Боковое ребро наклонной призмы длиной ℓ составляет с плоскостью
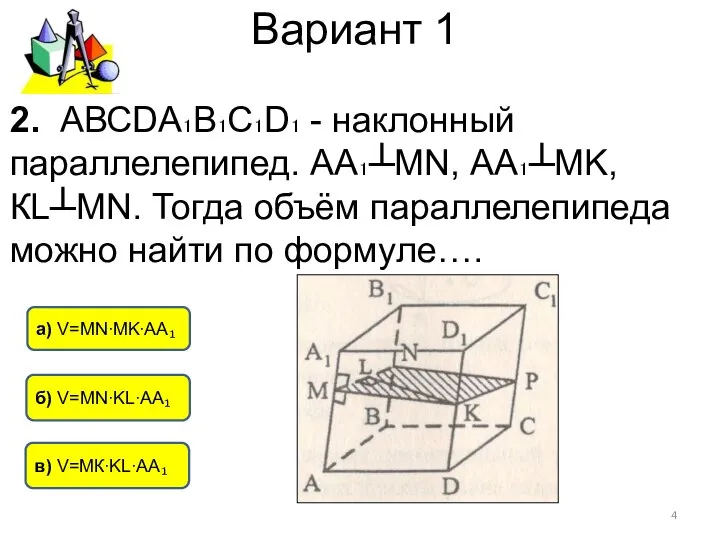
- 4. Вариант 1 б) V=МN∙KL∙АА₁ а) V=МN∙MK∙АА₁ в) V=МК∙KL∙АА₁ 2. АВСDА₁В₁С₁D₁ - наклонный параллелепипед. АА₁┴MN, АА₁┴MK, КL┴MN.
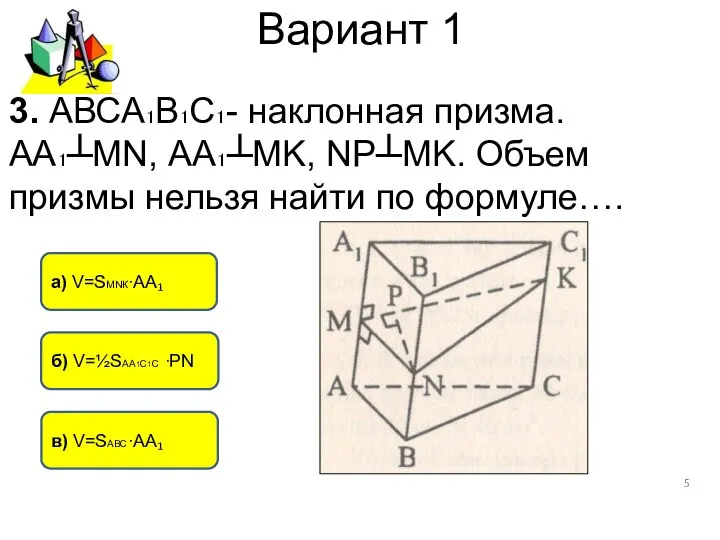
- 5. Вариант 1 в) V=SАВС∙АА₁ а) V=SMNК∙АА₁ б) V=½SАА1С1С ∙РN 3. АВСА₁В₁С₁- наклонная призма. АА₁┴MN, АА₁┴MK, NP┴MK.
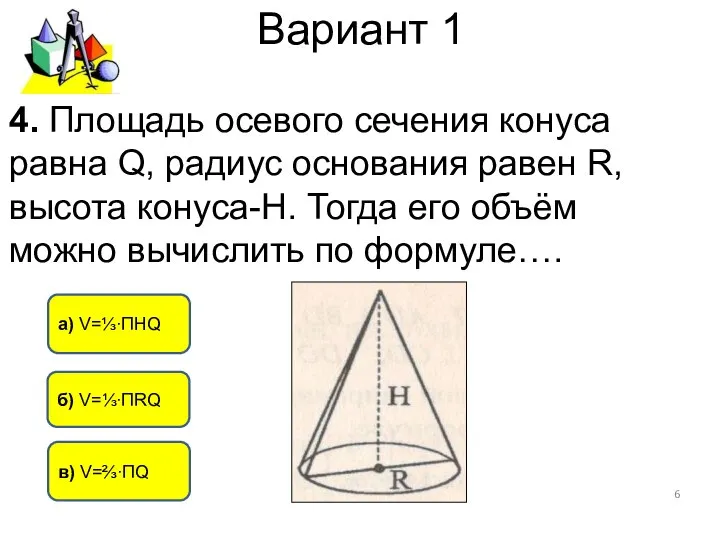
- 6. Вариант 1 б) V=⅓∙ПRQ в) V=⅔∙ПQ а) V=⅓∙ПНQ 4. Площадь осевого сечения конуса равна Q, радиус
- 7. Вариант 1 в) V=4/3∙Пℓ²Н, где ℓ- образующая конуса а) V=1/9∙ПН³, где Н – высота конуса 5.
- 8. Вариант 1 в) V=1/12∙ПН(d₁²+d₂²+d₁d₂), где d₁ и d₂ - диаметры оснований б) V=⅓∙H(M+N+MN), где M и
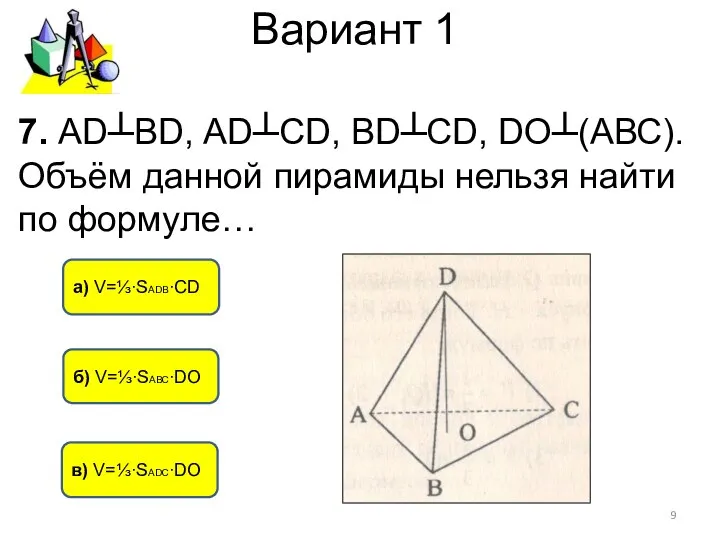
- 9. Вариант 1 в) V=⅓∙SАDС∙DО а) V=⅓∙SАDВ∙CD б) V=⅓∙SАВС∙DО 7. АD┴BD, АD┴СD, BD┴CD, DO┴(АВС). Объём данной пирамиды
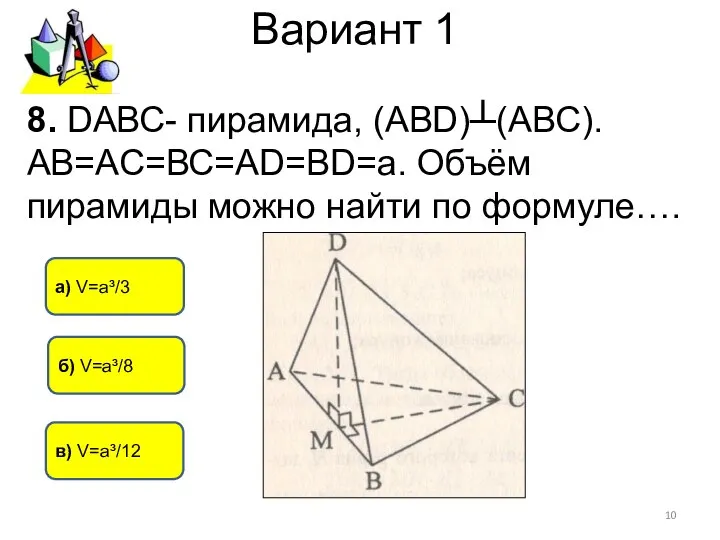
- 10. Вариант 1 б) V=а³/8 в) V=а³/12 а) V=а³/3 8. DАВС- пирамида, (АВD)┴(АВС). АВ=АС=ВС=АD=BD=а. Объём пирамиды можно
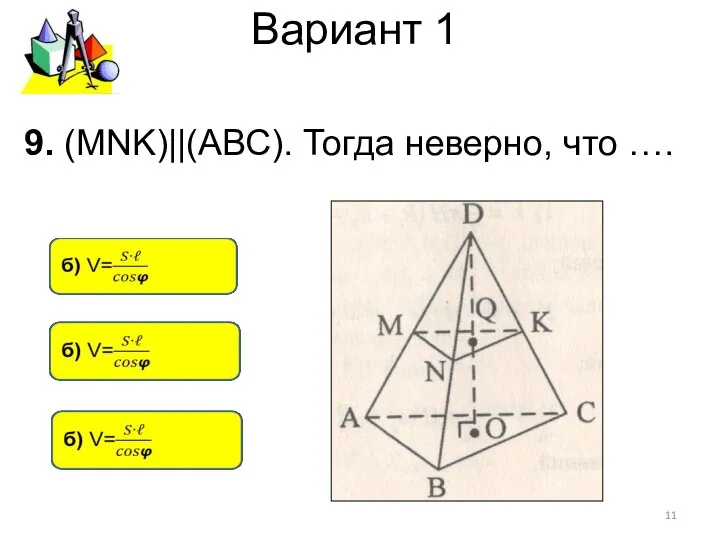
- 11. Вариант 1 9. (MNK)||(АВС). Тогда неверно, что ….
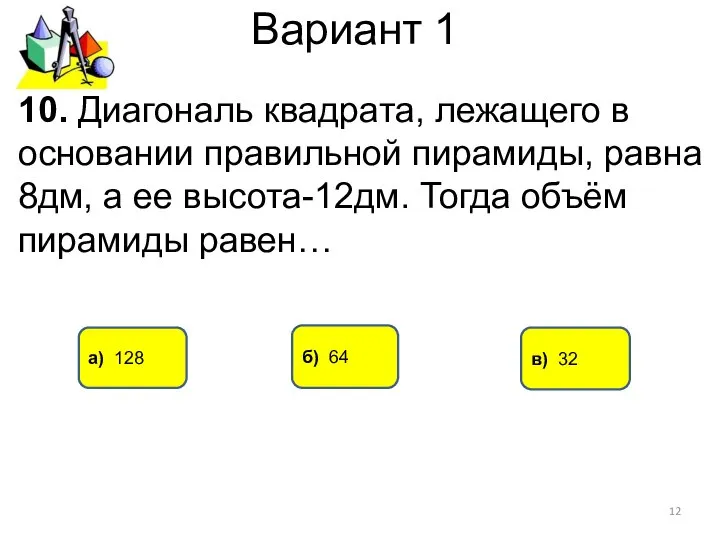
- 12. Вариант 1 а) 128 в) 32 10. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8дм,
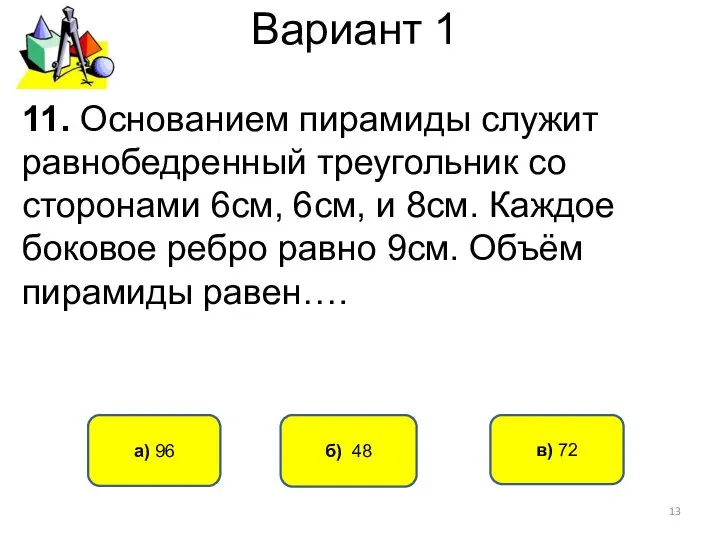
- 13. Вариант 1 б) 48 а) 96 11. Основанием пирамиды служит равнобедренный треугольник со сторонами 6см, 6см,
- 14. Вариант 1 б) 9 а) 18 12. Основанием пирамиды является ромб со стороной 6см. Каждый из
- 15. Вариант 1 в) 2000П а) 1600П б) 2000 13. Радиус основания конуса равен 20см, расстояние от
- 16. Вариант 1 а) 30 б) 15 в) 10 14. В наклонной призме основание – прямоугольный треугольник,
- 18. Скачать презентацию






 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Математический диктант. 6 класс
Математический диктант. 6 класс Числовые ряды
Числовые ряды Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Диофантово уравнение
Диофантово уравнение Векторы
Векторы Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Числовые головоломки
Числовые головоломки 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Regresní a korelační analýza
Regresní a korelační analýza Предел функции (часть 2)
Предел функции (часть 2)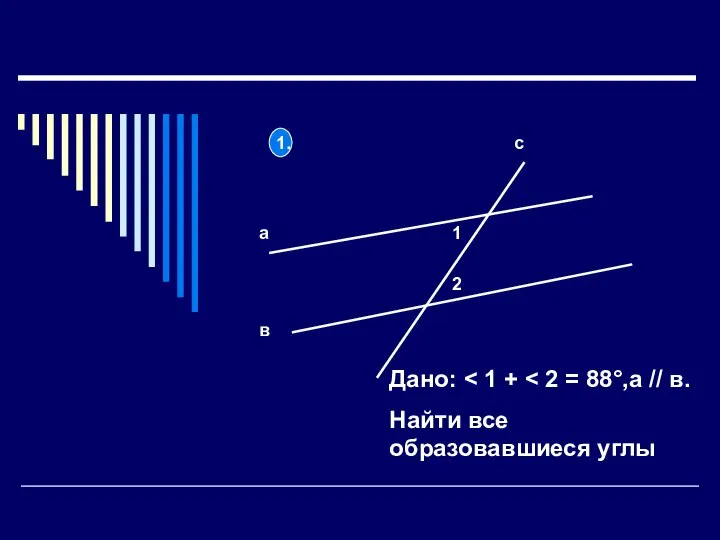 Признаки равенства треугольников
Признаки равенства треугольников Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Теорема Виета. Устная работа
Теорема Виета. Устная работа Минимизация переключательных функций
Минимизация переключательных функций Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС Сложение десятичных дробей
Сложение десятичных дробей