Тетраэдр параллелепипед. 10 класс

Тетраэдр и параллелепипед
Тетраэдр
Параллелепипед
Практика

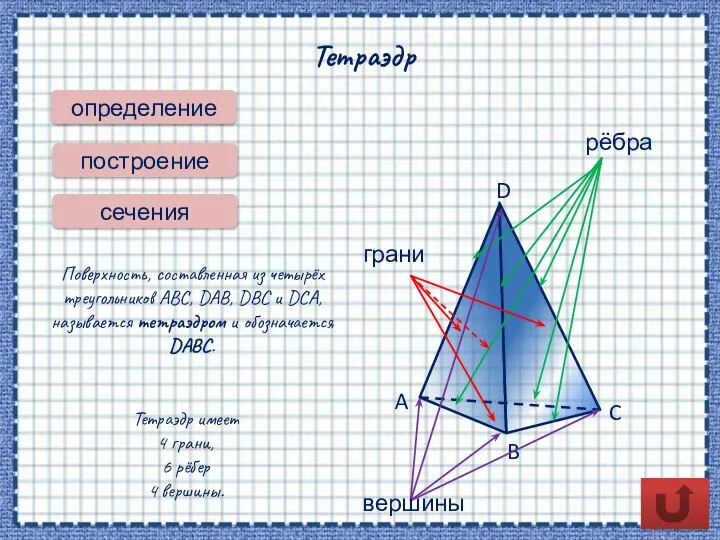
Тетраэдр
определение
сечения
Поверхность, составленная из четырёх треугольников ABC, DAB, DBC и DCA, называется тетраэдром и обозначается DABC.
D
A
B
C
грани
рёбра
вершины
Тетраэдр имеет
4 грани,
6 рёбер
4 вершины.
построение

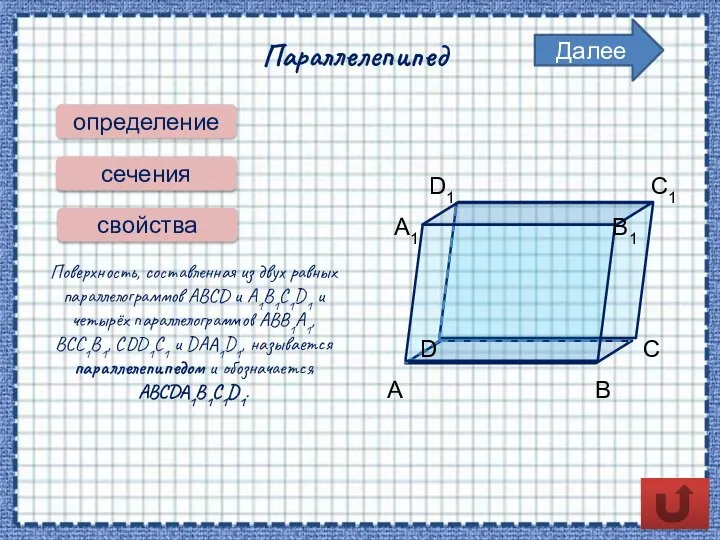
Параллелепипед
определение
сечения
Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырёх параллелограммов ABB1A1, BCC1B1, CDD1C1 и DAA1D1, называется параллелепипедом и обозначается ABCDA1B1C1D1.
свойства
D1 C1
A1 B1
D C
A B
Далее

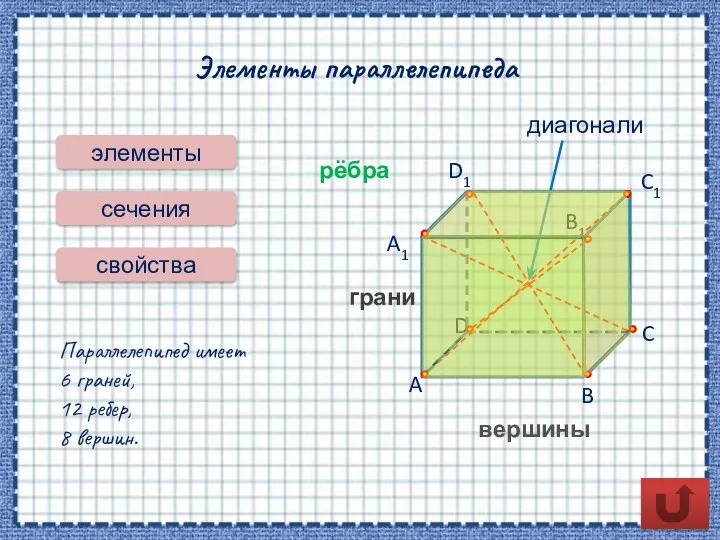
Элементы параллелепипеда
элементы
сечения
A
B
C
D
A1
D1
C1
B1
диагонали
свойства
грани
рёбра
вершины
Параллелепипед имеет
6 граней,
12 ребер,
8 вершин.

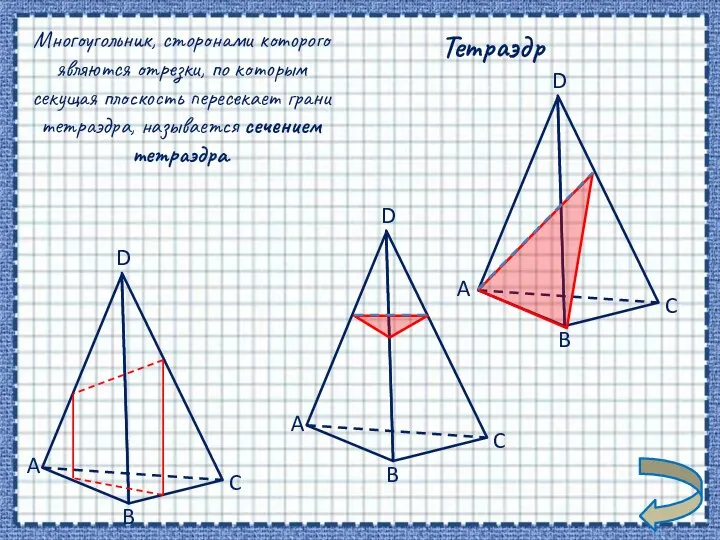
Тетраэдр
C
A
D
B
Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани тетраэдра, называется сечением тетраэдра.

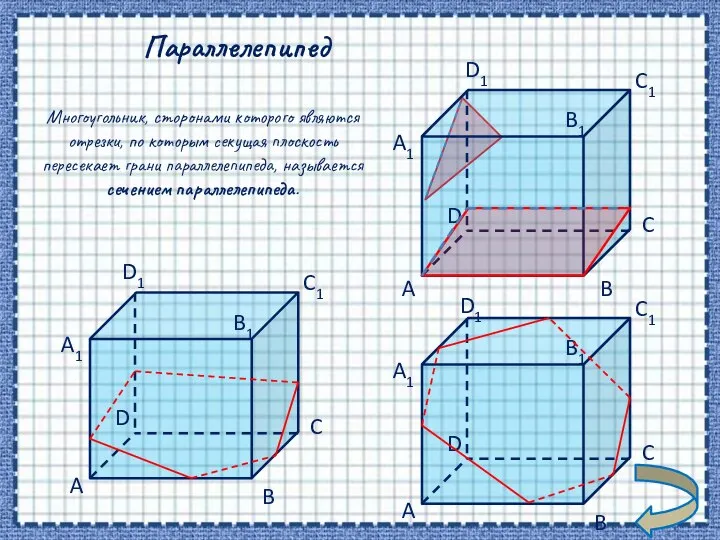
Параллелепипед
Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани параллелепипеда, называется сечением параллелепипеда.
D1

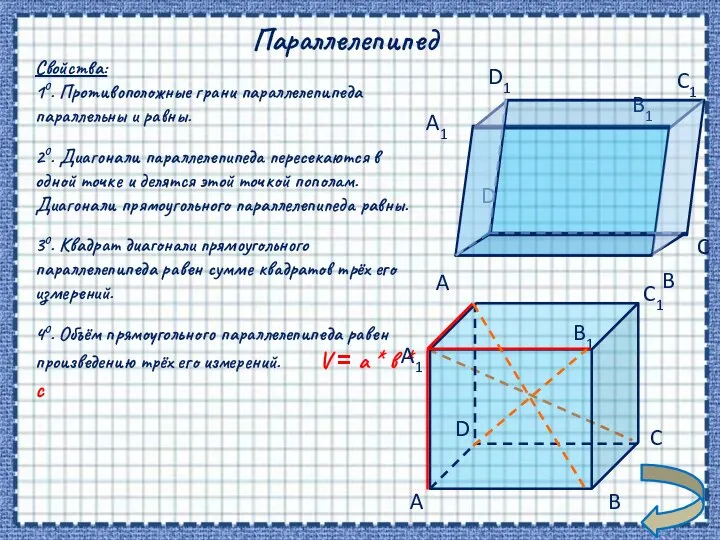
Параллелепипед
Свойства:
10. Противоположные грани параллелепипеда параллельны и равны.
20. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Диагонали прямоугольного параллелепипеда равны.
30. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
40. Объём прямоугольного параллелепипеда равен
произведению трёх его измерений. V = а * в * с
A1
A
B1
C1
D
B
C
D1

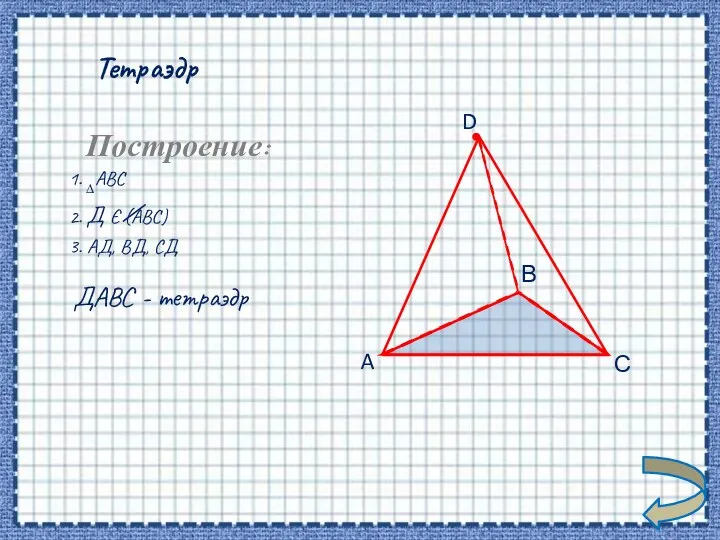
Тетраэдр
Построение:
1. ∆АВС
2. Д Є (АВС)
A
В
С
D
3. АД, ВД, СД
ДАВС - тетраэдр

Решение задач
№ 68 (устно)
№ 69
№ 70
№ 74
№ 79
№ 80