TOChEChNAYa_I_INTERVAL_NAYa_OTsENKA_SLUChAJNOJ_VELIChINY (1)

Одной из задач математической статистики, является определение параметров большого массива по исследованию его части.
Два вида оценки:
Точечная оценка случайной величины;
Интервальная оценка случайной величины.
ОЦЕНКИ ПАРАМЕТРОВ В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Рассмотрим изучение некоторого количественного признака X. Его распределение в генеральной совокупности характеризуется параметрами, называемыми числовыми характеристиками генеральной совокупности. К ним относятся генеральная средняя, генеральная дисперсия и генеральное среднее квадратическое отклонение.
Определение. Генеральной средней хг называется среднее арифметическое всех значений изучаемого признака в генеральной совокупности:

где N - объем генеральной совокупности; xi - значения признака для различных объектов генеральной совокупности с присвоенными им номерами i = 1, 2, N.
Можно показать, что генеральная средняя равна математическому ожиданию, но для определенности дальше мы будем пользоваться генеральной средней.
Как отмечалось ранее, рассчитать генеральную среднюю практически сложно или невозможно из-за большого объема генеральной совокупности, сложности измерений и проч. Поэтому для изучения генеральной совокупности из нее извлекают выборку относительно небольшого объема.
Определение. Выборочной средней хв называется среднее арифметическое всех значений изучаемого признака в выборке:

где n - объем выборки; xi - значения признака. Если некоторые значения xi встречаются несколько раз (т. е. соответствующие частоты mi > 1), то в сумму их следует подставлять столько же раз.
В математической статистике показывается, что в случае репрезентативной выборки математическое ожидание выборочной средней (для разных выборок) равно генеральной средней:
Для оценки генеральной средней, считается, что неизвестная генеральная средняя приблизительно равна рассчитанной выборочной средней:
Это точечная оценка генеральной средней. Точечной она называется потому, что характеризуется одним числом - точкой на числовой оси.

Определение. Генеральной дисперсией называется среднее арифметическое квадратов отклонений всех значений изучаемого признака X в генеральной совокупности от генеральной средней:
где xi - значения признака; хг - генеральная средняя.
Генеральная дисперсия характеризует среднее отклонение значений признака в генеральной совокупности относительно генеральной средней.
Рассчитать генеральную дисперсию практически очень сложно. Поэтому для ее оценки вычисляют соответствующие характеристики в выборке.

Определение. Выборочной дисперсией называется среднее арифметическое квадратов отклонений всех значений изучаемого признака в выборке относительно выборочной средней:
где xi - значение признака; хв - выборочная средняя. Если некоторые значения xt встречаются несколько раз (т. е. соответствующие частоты mi > 1), то в сумму их следует подставлять столько же раз.
Выборочная дисперсия характеризует среднее отклонение значений признака в выборке относительно выборочной средней.
Если данные представлены в виде интервального ряда распределения, то выборочную среднюю и выборочную дисперсию можно приближенно вычислить по следующим формулам:

Определение. Генеральным средним квадратическим отклонением σг, называется квадратный корень из генеральной дисперсии:
Определение. Выборочным средним квадратическим отклонением σв называется квадратный корень из выборочной дисперсии:

ИНТЕРВАЛЬНАЯ ОЦЕНКА. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ.
При достаточно большом объеме выборки можно сделать вполне надежные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема (n<30). При небольшом объеме выборки пользуются интервальными оценками. В этом случае указывается интервал (доверительный интервал).
Доверительный интервал – интервал, в котором с заданной доверительной вероятностью находится истинное значение случайной величины (среднее значение генеральной совокупности).
Доверительная вероятность – вероятность, с которой в заданном интервале (доверительном интервале) находится истинное значение случайной величины (среднее значение генеральной совокупности). Обычно в медико-биологических исследованиях доверительную вероятность принимают равной 0,95.

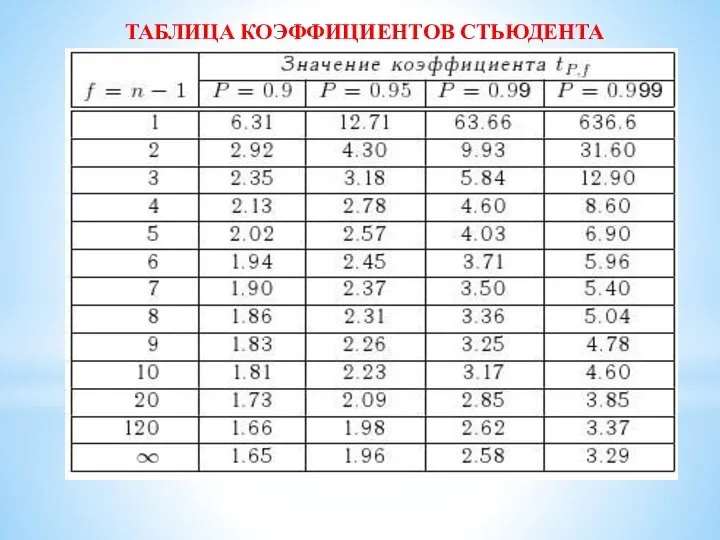
ТАБЛИЦА КОЭФФИЦИЕНТОВ СТЬЮДЕНТА

ЗАДАЧИ
Задача № 1 . При оценке жизненной емкости легких спринтеров был получен следующий вариационный ряд: (Xi, л) - 5, 6, 7, 8, 9; mi – 1, 2, 4, 3, 2. Найдите дисперсию данной случайной величины, если ее выборочное среднее равно 7,25 л.

Задача № 2. При исследования частоты дыхания гимнастов было установлено, что среднее квадратическое отклонение равно 1,1. Найдите выборочную дисперсию данного показателя.
Задача № 3. При исследования двигательных функциий каратистов было установлено, что выборочная дисперсия показателя теппинг-теста равна 1,69. Найдите среднее квадратическое отклонение данного показателя.
Решение:

Задача № 4. При исследовании скорости распространения механической волны на поражённых участках кожи у больных псориазом в регрессирующей стадии были получены следующие результаты, м/с: 38, 39, 41,41, 38, 43, 40, 40, 42, 38, 38, 39, 38, 41, 42, 41, 42, 41, 39, 43, 42, 43, 40, 39, 40, 38, 43, 42, 39, 42.
Дать точечную оценку распределения (рассчитать математическое ожидание, дисперсию, среднее квадратическое отклонение);
Дать интервальную оценку данного показателя на уровне доверительной вероятности α = 0,95.