Содержание
- 2. Дано: а⋂b ∠1=124 ° Решение: ∠1 и ∠2 – вертикальные, значит ∠1 = ∠2 = 124
- 3. Дано: ∠1 и ∠2 смежные ∠2 на 28 ° меньше ∠1 Решение: Пусть ∠1 = х°,
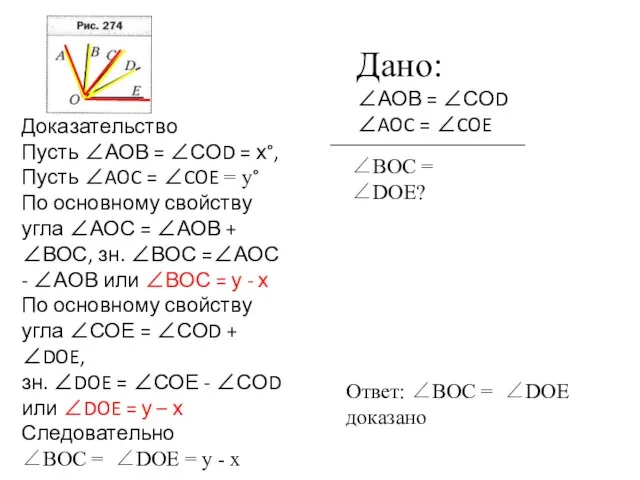
- 4. Дано: ∠АОВ = ∠СОD ∠AOC = ∠COE Доказательство Пусть ∠АОВ = ∠СОD = х°, Пусть ∠AOC
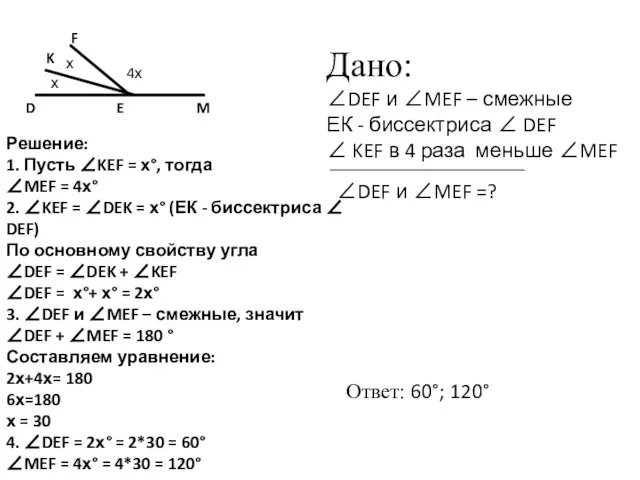
- 5. Дано: ∠DEF и ∠MEF – смежные ЕК - биссектриса ∠ DEF ∠ KEF в 4 раза
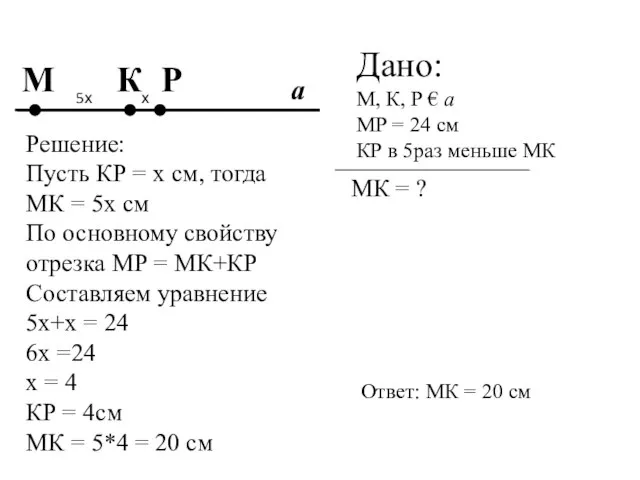
- 6. М Р К Дано: М, К, Р € а МР = 24 см КР в 5раз
- 8. Скачать презентацию


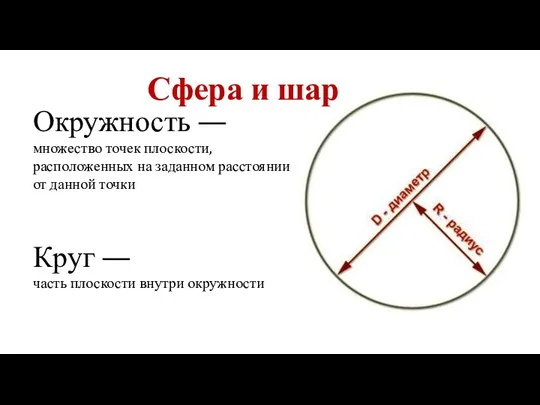 Сфера и шар
Сфера и шар Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Деление. Неправильные дроби
Деление. Неправильные дроби Геометрия в живописи
Геометрия в живописи Угол между прямой и плоскостью
Угол между прямой и плоскостью Задачи на прогрессию
Задачи на прогрессию Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Степенная функция
Степенная функция Уравнение Бернулли
Уравнение Бернулли Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Площадь поверхности цилиндра
Площадь поверхности цилиндра Параллельные прямые
Параллельные прямые Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики B7
B7 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2)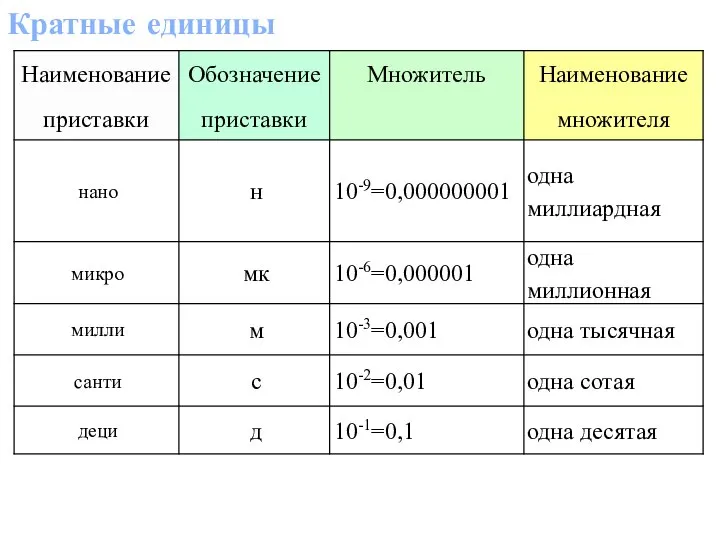 Кратные единицы
Кратные единицы Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Треугольники, задача
Треугольники, задача Прямоугольник
Прямоугольник Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Естественно балансирующееся общество
Естественно балансирующееся общество ریاضی جزوه کامل
ریاضی جزوه کامل Таблица Шульте
Таблица Шульте Понятие производной
Понятие производной Почти все об углах
Почти все об углах