Содержание
- 2. Метрология (метрон–мера, логос–учение (греч.)) – наука об измерениях, методах и средствах обеспечения их единства и способах
- 3. Основные задачи метрологии установления единиц измерений физических величин обеспечение единства измерений и единообразных средств измерений разработка
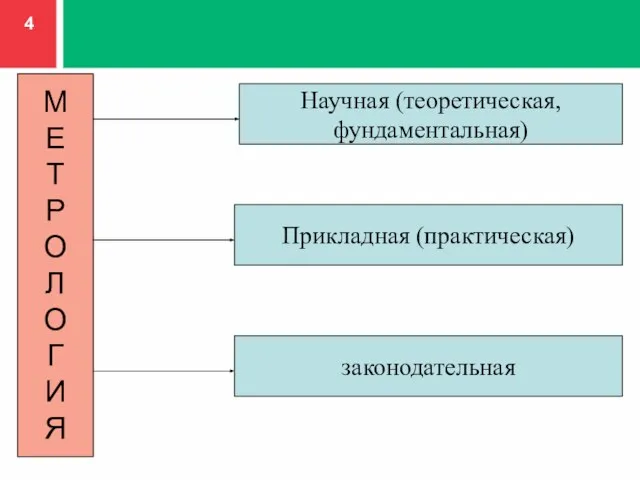
- 4. М Е Т Р О Л О Г И Я Прикладная (практическая) Научная (теоретическая, фундаментальная) законодательная
- 5. НАУЧНАЯ (теоретическая) Научная метрология занимается вопросами фундаментальных исследований, созданием систем единиц измерений, физических постоянных, разработкой новых
- 6. ПРИКЛАДНАЯ (практическая) Прикладная метрология занимается вопросами практического применения в различных сферах деятельности человека результатов теоретических исследований,
- 7. ЗАКОНОДАТЕЛЬНАЯ Законодательная метрология включает в себя совокупность взаимообусловленных правил и норм, направленных на обеспечение единства измерений,
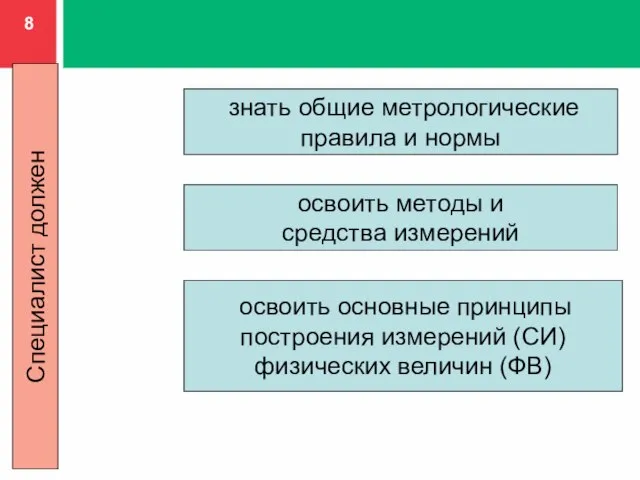
- 8. знать общие метрологические правила и нормы освоить методы и средства измерений освоить основные принципы построения измерений
- 9. Основные термины и определения Основные термины и определения к ним даны в официально задействованном на территории
- 10. Предметом метрологии является извлечение количественной информации о свойствах физических объектов и процессов с заданной точностью и
- 11. Все физические объекты окружающего нас материального мира отличаются друг от друга характерными им свойствами. Свойство есть
- 12. Для количественного описания различных свойств физических объектов вводится понятие величина. Величина есть свойство чего-либо, что может
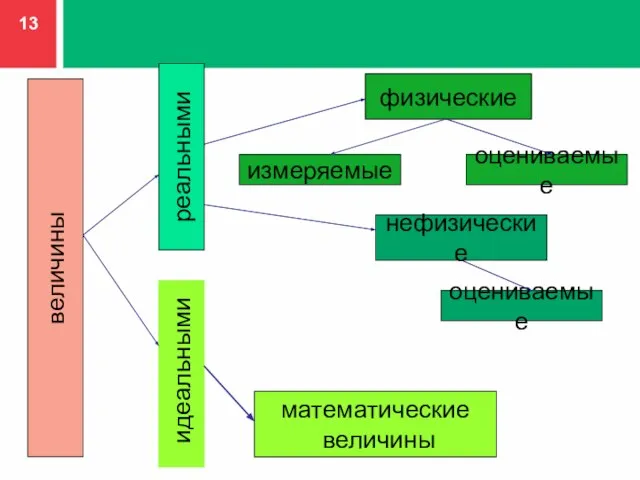
- 13. величины реальными идеальными нефизические физические математические величины измеряемые оцениваемые оцениваемые
- 14. Физическая величина определяется как величина, свойственная материальным объектам (веществам, изделиям, услугам, процессам и т.д.), изучаемым в
- 15. К нефизическим величинам относят величины, характеризующие общественно-гуманитарные науки (философия, филология, социология, история и т.д.) К идеальным
- 16. По рекомендации РМГ 29-99 физической величиной называется одно из свойств физического объекта (вещества, изделия, процесса, работ,
- 17. Согласно МИ 2247 – 93 Измерение ФВ – совокупность операций по применению технического средства, хранящего единицу
- 18. Физическая величина, подлежащая измерению, измеряемая или измеренная в соответствии с основной целью измерительной задачи ИЗМЕРЯЕМАЯ ФИЗИЧЕСКАЯ
- 19. Количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу РАЗМЕР ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ
- 20. это оценка ее размера в виде некоторого числа принятых для нее единиц измерений. ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ
- 21. отвлеченное число, выражающее отношение значения величины к соответствующей единице измерения данной физической величины. ЧИСЛОВОЕ ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ
- 22. Выражение вида Q= q[Q] называют основным уравнением измерения. q – число, полученное измерением; [Q] – ЕИ
- 23. Значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину. Примечание
- 24. Значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной
- 25. Физическая величина, оказывающая влияние на размер измеряемой величины и (или) результат измерений ВЛИЯЮЩАЯ ФИЗИЧЕСКАЯ ВЕЛИЧИНА
- 26. Совокупность физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимают за независимые, а
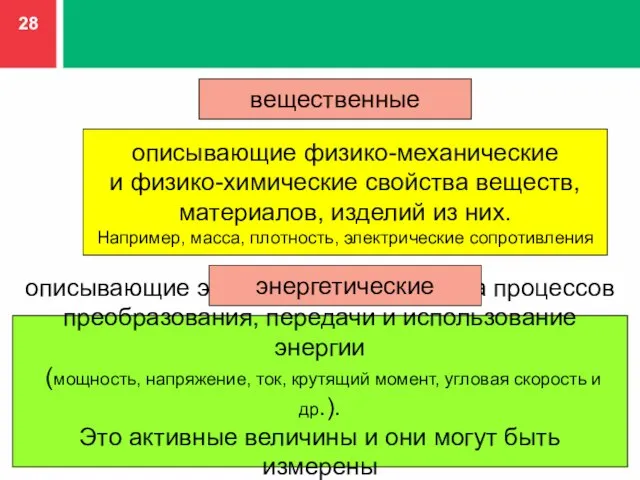
- 27. вещественные энергетические величины, характеризующие протекание процессов во времени. С целью изучения метрологических особенностей физические величины подразделяют
- 28. описывающие физико-механические и физико-химические свойства веществ, материалов, изделий из них. Например, масса, плотность, электрические сопротивления описывающие
- 29. величины, характеризующие протекание процессов во времени. к ним относятся корреляционные функции, показатели спектрального анализа веществ и
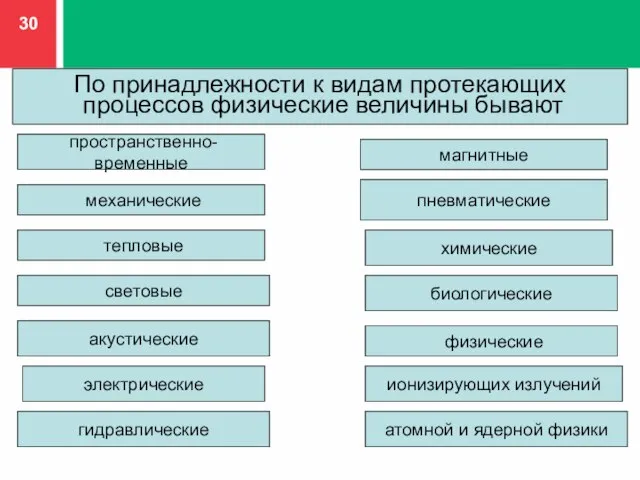
- 30. По принадлежности к видам протекающих процессов физические величины бывают пространственно-временные механические тепловые световые акустические электрические гидравлические
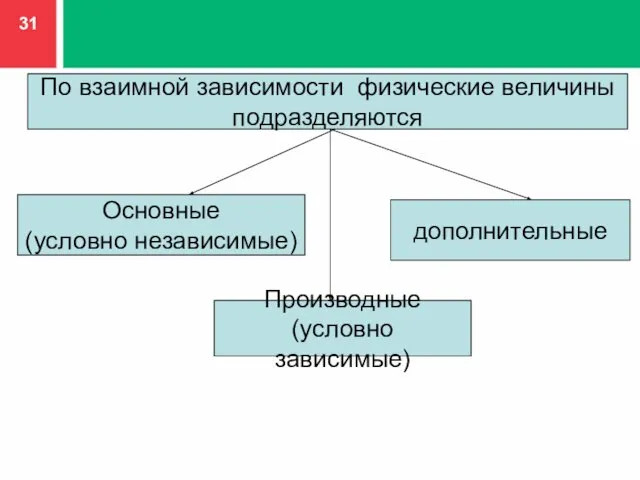
- 31. По взаимной зависимости физические величины подразделяются Основные (условно независимые) Производные (условно зависимые) дополнительные
- 32. ОСНОВНАЯ ФВ Физическая величина, входящая в систему величин и условно принятая в качестве независимой от других
- 33. Физическая величина, входящая в систему величин и определяемая через основные величины этой системы. ПРОИЗВОДНАЯ ФВ скорость
- 34. ДОПОЛНИТЕЛЬНЫЕ Термин "дополнительная единица" был введен в 1960 г. Дополнительными единицами являлись "радиан" и "стерадиан". XIX
- 35. РАЗМЕРНОСТЬ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ Выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в
- 36. Примечания 1. Степени символов основных величин, входящих в одночлен, в зависимости от связи рассматриваемой физической величины
- 37. 2. В соответствии с международным стандартом ИСО 31/0, размерность величин следует обозначать знаком dim (dimension). В
- 38. ПОКАЗАТЕЛЬ РАЗМЕРНОСТИ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ Показатель степени, в которую возведена размерность основной физической величины, входящая в размерность
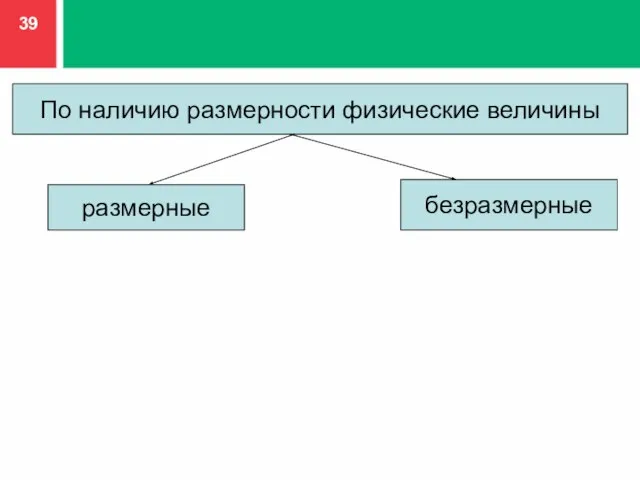
- 39. По наличию размерности физические величины размерные безразмерные
- 40. РАЗМЕРНАЯ Физическая величина, в размерности которой хотя бы одна из основных физических величин возведена в степень,
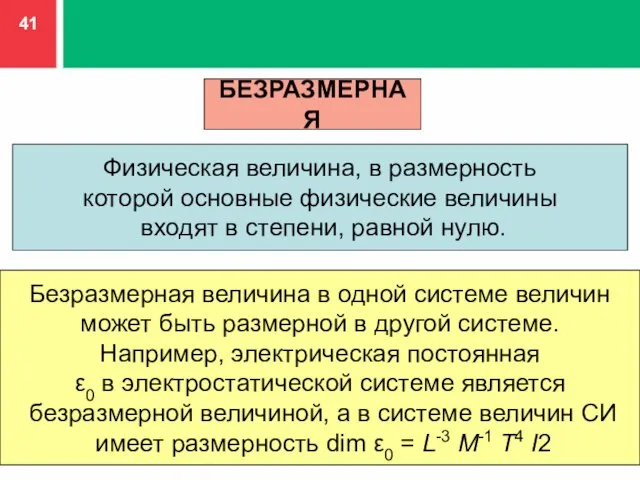
- 41. БЕЗРАЗМЕРНАЯ Физическая величина, в размерность которой основные физические величины входят в степени, равной нулю. Безразмерная величина
- 42. Совокупность, основных, дополнительных и производных единиц измерений ФВ, образованная в соответствии с принятыми принципами называется системой
- 43. До настоящего времени во всех странах мира cоздавались и применялись различные системы измерений ФВ (СГС, МКГСС,
- 44. Генеральные конференции по мерам и весам, международные конференции представителей стран- участниц Метрической конвенции , созываемые не
- 45. К 1970 состоялось 13 конференций, на них был принят ряд важных решений. 1-я конференция (1889) установила
- 46. На 7-й конференции (1927) установлено соотношение между метром и длиной световой волны красной линии кадмия и
- 47. 11-я конференция (1960) утвердила Международную систему единиц - СИ, приняла определение метра через длину световой волны
- 48. ШКАЛЫ ИЗМЕРЕНИЙ Упорядоченная совокупность значений физической величины, служащая исходной основой для измерений данной величины Международная температурная
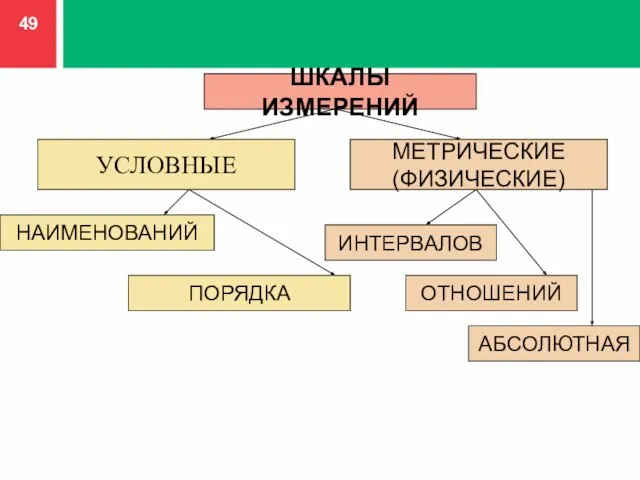
- 49. ШКАЛЫ ИЗМЕРЕНИЙ УСЛОВНЫЕ МЕТРИЧЕСКИЕ (ФИЗИЧЕСКИЕ) НАИМЕНОВАНИЙ ПОРЯДКА ИНТЕРВАЛОВ ОТНОШЕНИЙ АБСОЛЮТНАЯ
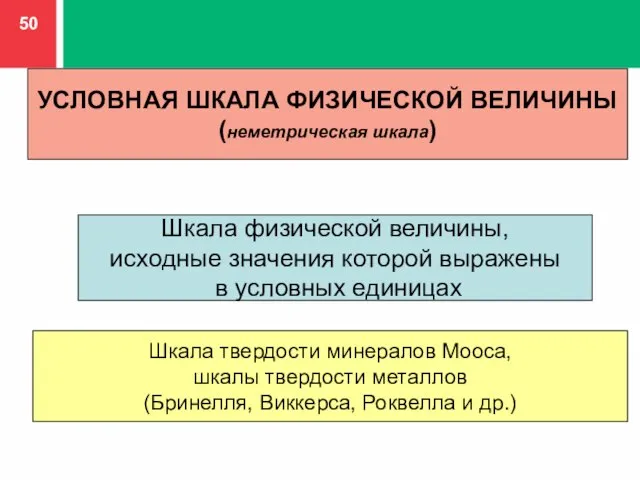
- 50. Шкала физической величины, исходные значения которой выражены в условных единицах УСЛОВНАЯ ШКАЛА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ (неметрическая шкала)
- 51. ШКАЛА НАИМЕНОВАНИЙ характеризуется только отношением эквивалентности различных качественных свойств ФВ. Такие шкалы не имеют начала отсчета,
- 52. ШКАЛА ПОРЯДКА описывает свойства физических величин, как отношением эквивалентности, так и отношением порядка по возрастанию или
- 53. Отправным (реперным) точкам ранжированного ряда могут быть поставлены цифры, называемые баллами и тогда появится возможность оценки,
- 54. По таким шкалам до сих пор оцениваются интенсивность сейсмических волн при землетрясениях, морское волнение, твердость минералов,
- 55. описывает свойства ФВ не только с помощью отношений эквивалентности и порядка, но и с применением суммирования
- 56. Примерами шкал интервалов являются шкалы температур. На температурной шкале Цельсия за начало отсчета разности температур принята
- 57. Результаты измерений по шкале интервалов можно складывать друг с другом и вычитать друг из друга, т.е.
- 58. ШКАЛА ОТНОШЕНИЙ представляет собой интервальную шкалу с естественным началом. Если, например, за начало температурной шкалы принять
- 59. В общем случае, при сравнении между собой двух величин значения п образуют шкалу отношений. Она охватывает
- 60. АБСОЛЮТНАЯ ШКАЛА. Она обладает всеми признаками шкал отношений, но дополнительно имеет естественное однозначной определение единицы измерения
- 61. Практическая реализация шкал измерений осуществляется путем стандартизации самих шкал и единиц измерений.
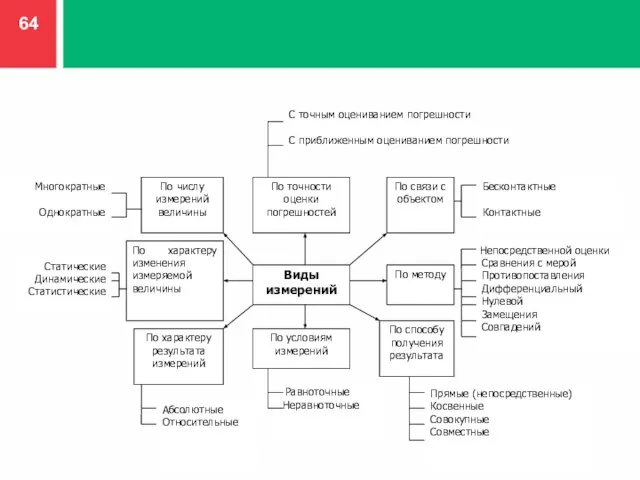
- 62. Измерения, как экспериментальные процедуры, разнообразны и классифицируются по разным признакам (РМГ 29-99): ВИДЫ ИЗМЕРЕНИЙ И ИХ
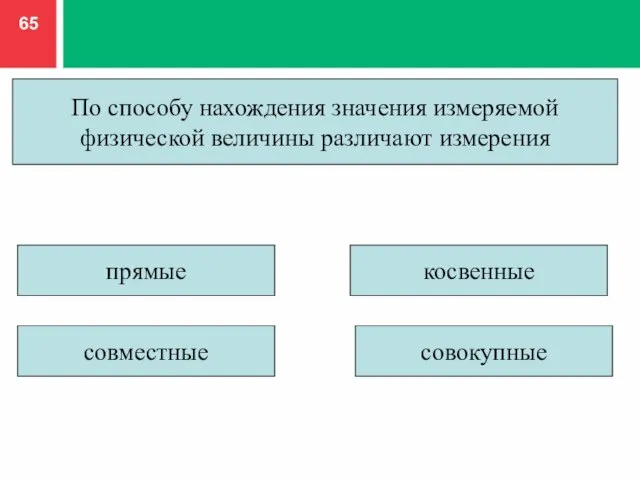
- 65. По способу нахождения значения измеряемой физической величины различают измерения прямые совместные совокупные косвенные
- 66. ПРЯМОЕ ИЗМЕРЕНИЕ это измерение, при котором искомое значение физической величины находят непосредственно по показаниям СИ.
- 67. КОСВЕННОЕ ИЗМЕРЕНИЕ измерение, при котором искомое значение физической величины находят расчетом на основании известной функциональной зависимости
- 68. СОВМЕСТНЫЕ ИЗМЕРЕНИЯ одновременные измерения двух или нескольких разнородных физических величин для установления функциональной зависимости между ними.
- 69. СОВОКУПНЫЕ ИЗМЕРЕНИЯ производимые одновременно нескольких одноименных величин, при которых искомые значения физической величины находят решением системы
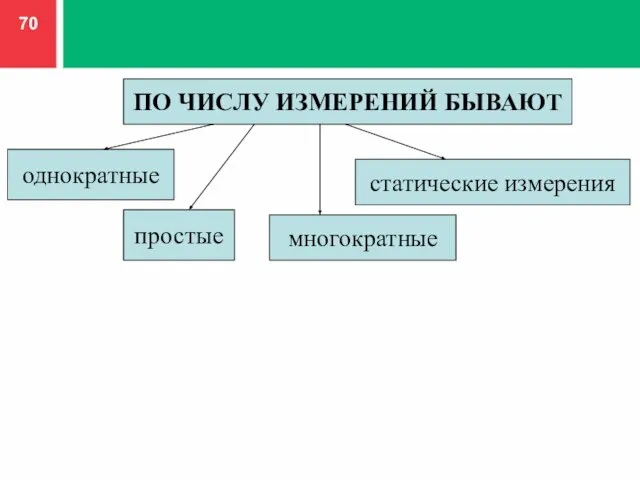
- 70. ПО ЧИСЛУ ИЗМЕРЕНИЙ БЫВАЮТ однократные статические измерения простые многократные
- 71. Любое СИ, как материальная система, обладает определенной инерционностью (механической, тепловой, электрической и т.д.) и, следовательно, не
- 72. Поэтому при измерении переменной физической величины инерционность СИ приводит к некоторому отставанию показаний СИ от истинного
- 73. Очевидно, что это отставание будет зависеть не только от инерционных свойств СИ, но и от скорости
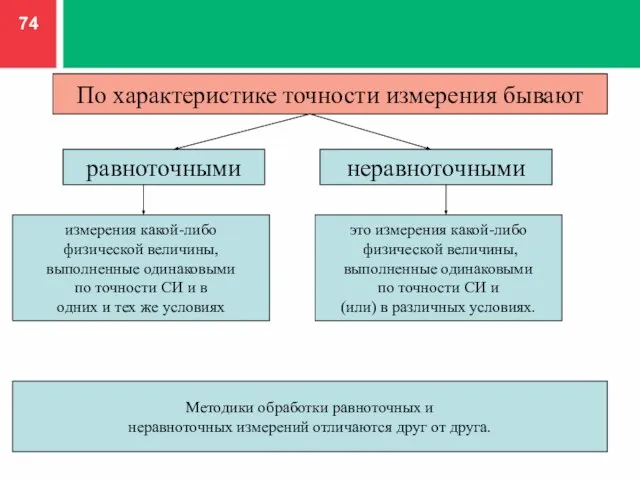
- 74. Методики обработки равноточных и неравноточных измерений отличаются друг от друга. По характеристике точности измерения бывают равноточными
- 75. По зависимости от метрологического назначения измерения ТЕХНИЧЕСКИЕ МЕТРОЛОГИЧЕСКИЕ
- 76. Метрологические измерения выполняют с помощью эталонных СИ с целью воспроизведения единицы измерения физической величины для передачи
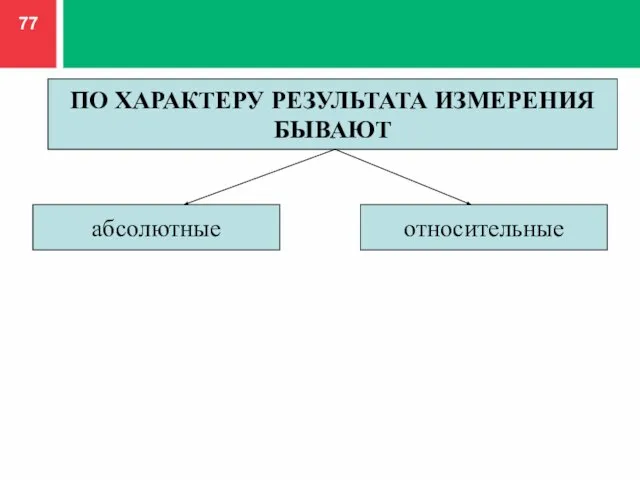
- 77. ПО ХАРАКТЕРУ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ БЫВАЮТ абсолютные относительные
- 78. АБСОЛЮТНОЕ ИЗМЕРЕНИЕ есть измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании
- 79. ОТНОСИТЕЛЬНОЕ ИЗМЕРЕНИЕ измерение отношения величины к одноименной величине, играющей роль единицы измерения, или измерения величины по
- 80. КОНТАКТНЫЙ основан на том, чувствительный элемент прибора приводится в контакт с объектом измерения. Например, контроль температуры
- 81. БЕСКОНТАКТНЫЙ ВИД основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения. Например,
- 82. Выбор того или иного метода измерений определяется назначением их результатов, требованиями к точности и быстроте реализации
- 83. Могут быть применены еще и нетрадиционные виды измерений в случаях, когда приходится использовать уникальные наблюдения за
- 84. Такие методы используют при физико-химических исследованиях быстропротекающих процессов взаимодействия элементарных частиц в ядерной реакции составляет около
- 85. МЕТОДЫ ИЗМЕРЕНИЙ Методом измерений называется прием или совокупность использованных приемов сравнения измеряемой физической величины с ее
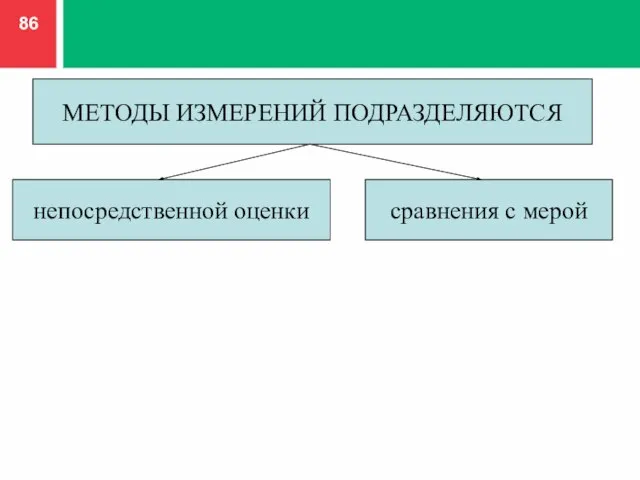
- 86. МЕТОДЫ ИЗМЕРЕНИЙ ПОДРАЗДЕЛЯЮТСЯ непосредственной оценки сравнения с мерой
- 87. Использование метода непосредственной оценки позволяет определить значения физической величины непосредственно по отсчетному устройству показывающего СИ (амперметр,
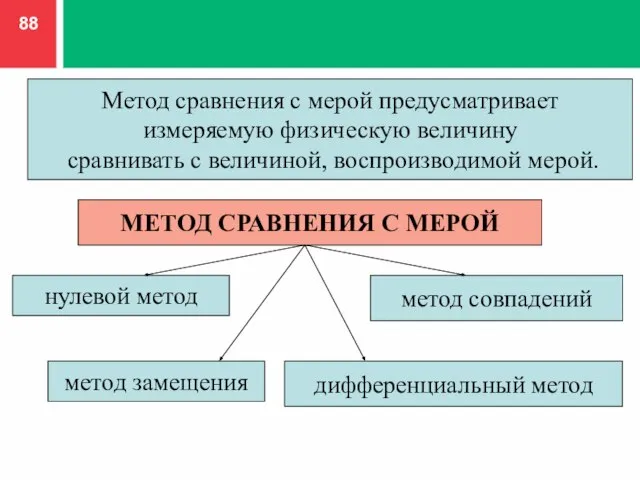
- 88. Метод сравнения с мерой предусматривает измеряемую физическую величину сравнивать с величиной, воспроизводимой мерой. МЕТОД СРАВНЕНИЯ С
- 89. НУЛЕВОЙ МЕТОД (МЕТОД ПОЛНОГО УРАВНОВЕШИВАНИЯ) метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой физической
- 90. ПРИ ДИФФЕРЕНЦИАЛЬНОМ МЕТОДЕ ПОЛНОЕ УРАВНОВЕШИВАНИЕ НЕ ПРОИЗВОДЯТ, А РАЗНОСТЬ МЕЖДУ ИЗМЕРЯЕМОЙ ВЕЛИЧИНОЙ И ВЕЛИЧИНОЙ, ВОСПРОИЗВОДИМОЙ МЕРОЙ,
- 91. Например, измерение массы на равноплечих весах, когда воздействие массы mx на весы частично уравновешивается массой гирь
- 92. метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. МЕТОД ЗАМЕЩЕНИЯ Например,
- 93. В МЕТОДЕ СОВПАДЕНИЙ разность между измеряемой величиной и величиной, воспроизводимой мерой, определяют, использую совпадения отметок шкал.
- 94. ПОГРЕШНОСТИ Погрешность измерения – отклонение результата измерения, которым является измеренное значение физической величины, от истинного (действительного)
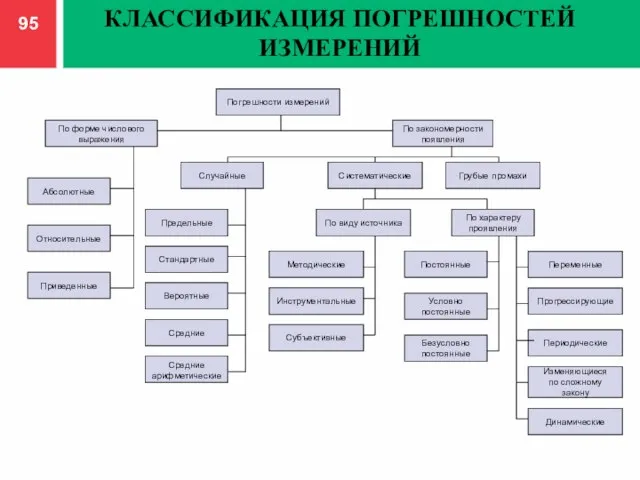
- 95. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
- 96. Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины:
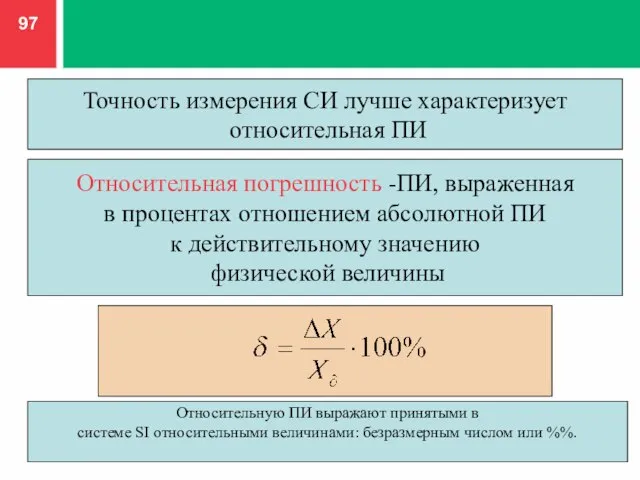
- 97. Точность измерения СИ лучше характеризует относительная ПИ Относительная погрешность -ПИ, выраженная в процентах отношением абсолютной ПИ
- 98. Приведенная ПИ есть отношение абсолютной ПИ к нормирующему значению Нормирующее значение измеряемой физической величины есть значение,
- 99. Практически используемой при производстве измерений и наиболее точно характеризующей несовершенство СИ является точность измерения. Точность измерения
- 100. Будучи важнейшей характеристикой результата измерения, определяющей степень доверия к нему, ПИ должна быть обязательно оценена. В
- 101. есть составляющая ПИ, изменяющаяся случайным образом, причем, случайно в вероятностно-статистическом смысле, при повторных измерениях одной и
- 102. Основными источниками случайных ПИ являются конструктивное несовершенство СИ, применяемого при измерении, принятие определенных числовых значений измеренных
- 103. МЕТОДИЧЕСКАЯ ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ составляющая погрешности измерений, Обусловленная несовершенством метода измерений. К ней относят погрешности, обусловленные отличием
- 104. Примерами методических погрешностей измерений являются: • погрешности изготовления цилиндрического тела (отличие от идеального круга) при измерении
- 105. • погрешность измерений вследствие кусочно-линейной аппроксимации нелинейной калибровочной зависимости СИ при вычислении результата измерений; • погрешность
- 106. ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ составляющая погрешности измерения, обусловленная несовершенством применяемого СИ: отличием реальной функции преобразования прибора от
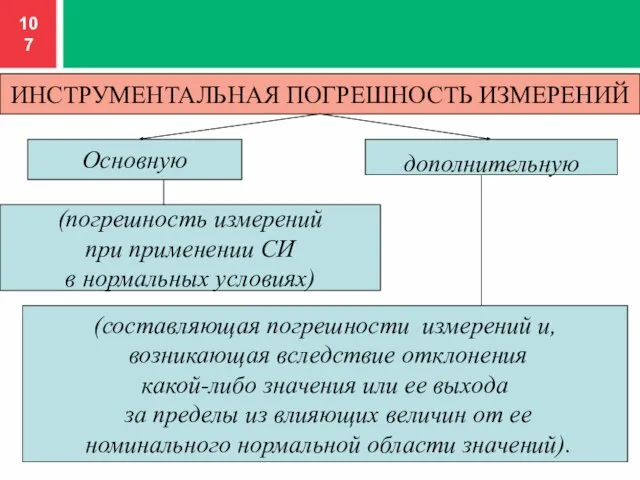
- 107. ИНСТРУМЕНТАЛЬНАЯ ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ Основную дополнительную (погрешность измерений при применении СИ в нормальных условиях) (составляющая погрешности измерений
- 108. Субъективная (личная) погрешность измерения составляющим погрешности измерения, обусловленная индивидуальными особенностями оператора, т. е. погрешность отсчета оператором
- 109. Характеристики субъективной погрешности измерений определяют с учетом способности «среднего оператора» к интерполяции в пределах цены деления
- 110. ПРОГРЕССИРУЮЩАЯ (ДРЕЙФОВАЯ) ПОГРЕШНОСТЬ это непредсказуемая погрешность, медленно меняющаяся во времени. Отличительные особенности прогрессирующих погрешностей: они могут
- 111. Прогрессирующая погрешность — это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не
- 112. ДИНАМИЧЕСКАЯ ПОГРЕШНОСТЬ это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной
- 113. СТАТИЧЕСКАЯ ПОГРЕШНОСТЬ это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.
- 114. ПРОМАХИ Промахами (грубыми ПИ) называют ПИ, существенно превышающие ожидаемые при данных условиях систематические и случайные ПИ.
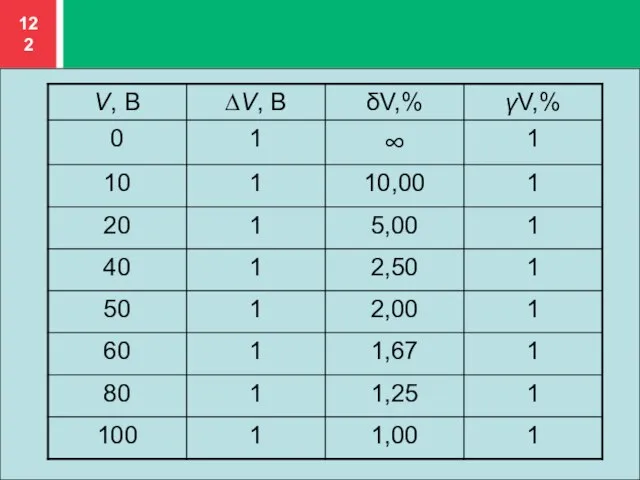
- 115. Вольтметром со шкалой (0…100) В, имеющим абсолютную погрешность ∆V =1 В, измерены значения напряжения 0; 10;
- 116. Решение. Для записи результатов формируем таблицу (табл. 1.1), в столбцы которой будем записывать измеренные значения V,
- 117. При V = 0 В получаем При V = 10 В получаем
- 118. Значения относительной погрешности для остальных измеренных значений напряжения рассчитываются аналогично. Полученные таким образом значения относительной Погрешности
- 119. Предварительно определим нормирующее значение VN. Так как диапазон измерений вольтметра – (0…100) В, то шкала вольтметра
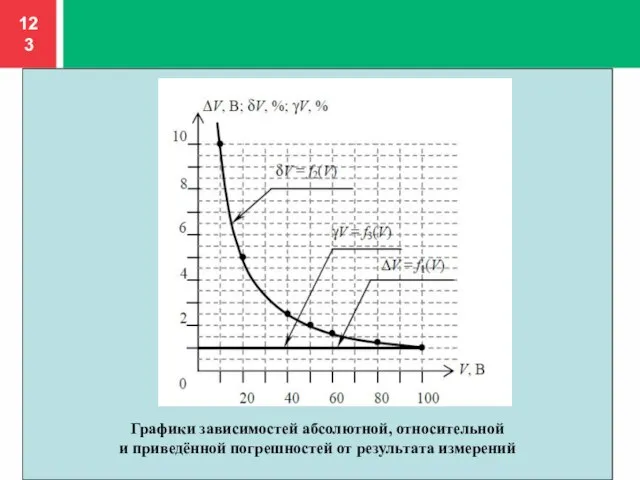
- 120. Это значение заносим во все ячейки четвёртого столбца. По данным табл. строим графики зависимостей абсолютной ∆V,
- 121. так как диапазон измерений прибора – (0…100) В, то за пределы этого диапазона построенные графики не
- 123. Графики зависимостей абсолютной, относительной и приведённой погрешностей от результата измерений
- 124. Задача 1. Омметром со шкалой (0...1000) Ом измерены значения 0; 100; 200; 400; 500; 600; 800;
- 125. Задача 2. Амперметром со шкалой (0…50) А, имеющим относительную погрешность δI = 2%, измерены значения силы
- 126. Задача 3. Вольтметром со шкалой (0…50) В, имеющим приведенную погрешность γV = 2%, измерены значения напряжения
- 127. Задача 4. Кислородомером со шкалой (0...25) % измерены следующие значения концентрации кислорода: 0; 5; 10; 12,5;
- 128. Задача 5. Расходомером со шкалой (0…150) м3/ч, имеющим относительную погрешность δQ = 2%, измерены значения расхода
- 129. Задача 6. Уровнемером со шкалой (5…10) м, имеющим приведенную погрешность γH = 1%, измерены значения уровня
- 130. Задача 7. Омметром со шкалой (0...20) кОм измерены значения 0; 1; 4; 5; 10; 12; 17;
- 131. Задача 8. Амперметром со шкалой (0…150) А, имеющим относительную погрешность δI = 4%, измерены значения силы
- 132. Задача 9. Вольтметром со шкалой (0…100) мВ, имеющим приведённую погрешность γV = 2%, измерены значения напряжения
- 133. Задача 10. Кислородомером со шкалой (0...50) % измерены следующие значения концентрации кислорода: 0; 5; 10; 15;
- 134. Задача 11. Расходомером со шкалой (0…230) м3/ч, имеющим относительную погрешность δQ = 6%, измерены значения расхода
- 135. Задача 12. Уровнемером со шкалой (1…20) м, имеющим приведённую погрешность γH = 1%, измерены значения уровня
- 136. Задача 13. Мегомметром со шкалой (0...150) МОм измерены следующие значения сопротивления: 0; 15; 30; 45; 60;
- 137. Задача 14. Амперметром со шкалой (0…50) А, имеющим приведённую погрешность γI = 0,2%, измерены значения силы
- 138. Задача 15. Вольтметром со шкалой (–50…50) В, имеющим приведенную погрешность γV = 2%, измерены значения напряжения
- 139. Задача 16. Кислородомером со шкалой (0...25) % измерены следующие значения концентрации кислорода: 0; 5; 10; 12,5;
- 140. Задача 17. Расходомером со шкалой (0…50) м3/ч, имеющим абсолютную погрешность ∆Q = 1 м3/ч, измерены значения
- 141. Задача 18. Уровнемером со шкалой (0…10) м, имеющим приведённую погрешность γH = 4%, измерены значения уровня
- 142. Задача 19. Омметром со шкалой (0...5000) Ом измерены значения 0; 500; 800; 1000; 1500; 2500; 3500;
- 143. Задача 20. Термометром со шкалой (–50…70) °С, имеющим абсолютную погрешность DТ = 1 °С, измерены значения
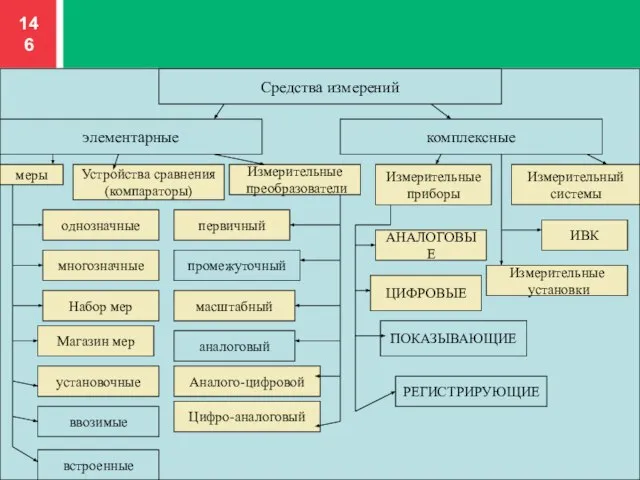
- 144. Средства измерений. Классификация средств измерений техническое средство, предназначено для измерений, имеющее нормированные метрологические характеристики, воспроизводящее или
- 145. Под метрологической характеристикой СИ понимают такие показатели, которые позволяют судить об их пригодности для измерений в
- 146. Средства измерений элементарные комплексные меры Устройства сравнения (компараторы) Измерительные преобразователи однозначные многозначные Набор мер Магазин мер
- 147. Мера - это средство измерений, предназначенное для воспроизведения физической величины заданного размера. Многозначная мера Мера, воспроизводящая
- 148. Набор мер Специально подобранный комплект мер, применяемый не только по отдельности, но и в различных сочетаниях
- 149. Магазин мер это набор мер, конструктивно объединенных в единое устройство, в котором имеются приспособления для их
- 150. Установочная мера физической величины мера физической величины, предназначенная: - для приведения показания или выходного сигнала средства
- 151. Средство сравнения Техническое средство или специально созданная среда, посредством которых возможно выполнять сравнение друг с другом
- 152. Измерительный прибор - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного
- 153. Измерительный преобразователь - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи,
- 154. Первичный измерительный преобразователь конструктивно оформленный как обособленное средства измерений с нормированной функцией преобразования, называется датчиком Датчик
- 155. АЦП служит для измерения напряжения, т.е. преобразования аналоговой информации в цифру. ЦАП представляет собой преобразователь входной
- 156. Цифровой измерительный прибор Измерительный прибор, автоматически вырабатывающий дискретные сигналы измерительной информации, показания которого представлены в цифровой
- 157. Масштабный преобразователь измерительный преобразователь, предназначенный для изменения величины в заданное число раз.
- 158. Измерительная установка - совокупность функционально объединенных средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств,
- 159. Измерительная система - совокупность средств измерений и вспомогательных устройств, соединенных между собой каналами связи, предназначенная для
- 160. Измерительно – вычислительный комплекс Функционально объединённая совокупность средств измерений, ЭВМ и вспомогательных устройств, предназначенная для выполнения
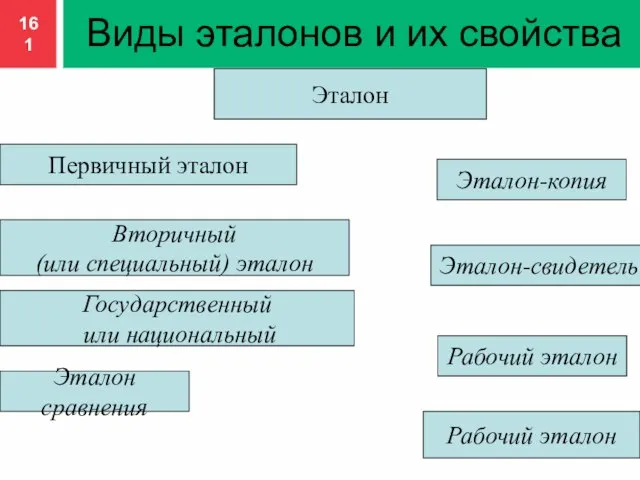
- 161. Виды эталонов и их свойства Эталон Первичный эталон Рабочий эталон Эталон сравнения Эталон-копия Эталон-свидетель Государственный или
- 162. Первичный эталон - эталон, обеспечивающий воспроизведение единицы с наивысшей в стране (по сравнению с другими эталонами
- 163. Вторичные эталоны по своему назначению делятся на эталоны сравнения эталоны-копии эталоны-свидетели и рабочие эталоны
- 164. Государственный или национальный - это первичный или специальный эталон, официально утвержденный в качестве исходного для страны.
- 165. Эталон-копия предназначен для передачи размеров единиц рабочим эталонам. Он не всегда является физической копией государственного эталона.
- 167. Скачать презентацию

















![Выражение вида Q= q[Q] называют основным уравнением измерения. q – число, полученное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/872618/slide-21.jpg)


























































































































 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов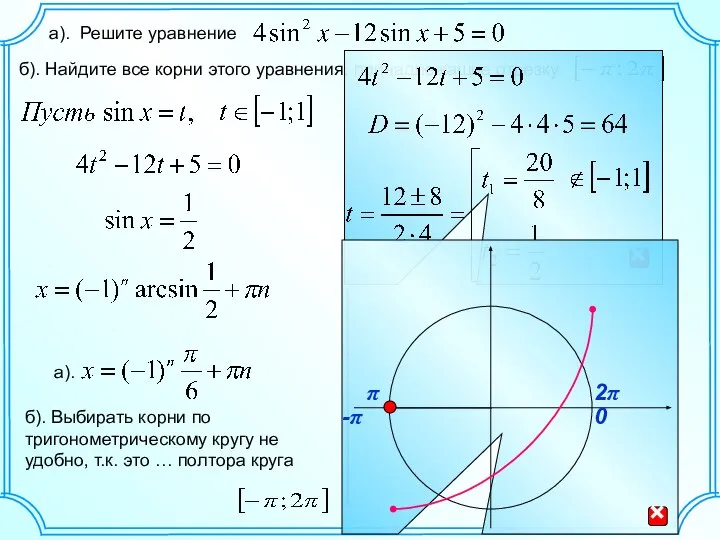 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители