Плоскость в пространстве

Общее уравнение плоскости
Если в пространстве фиксирована произвольная декартова система координат Oxyz, то всякое уравнение первой степени с тремя переменными x y z определяет относительно этой системы плоскость.
A; B; C; D – некоторые постоянные, причем из чисел A; B; C хотя бы одно отлично от нуля.
(1)
Общее уравнение плоскости
Пусть точка М0(x0; y0; z0) принадлежит плоскости:
(2)
Вычтем из уравнения (1) тождество (2):
(3)
Общее уравнение плоскости

Общее уравнение плоскости
Произвольная точка М(x; y; z) лежит на плоскости, если ее координаты удовлетворяют уравнению (3):
М0
М
Уравнение (3) является условием перпендикулярности двух векторов:
и
Таким образом, точка М лежит в плоскости, если
Нормальный вектор плоскости
Общее уравнение плоскости называется полным, если все коэффициенты А; B; C; D отличны от нуля.
В противном случае уравнение называется неполным.

Общее уравнение плоскости
1)
Виды неполных уравнений:
2)
3)
4)
5)
Плоскость проходит через точку О.
6)
7)
8)
9)
10)

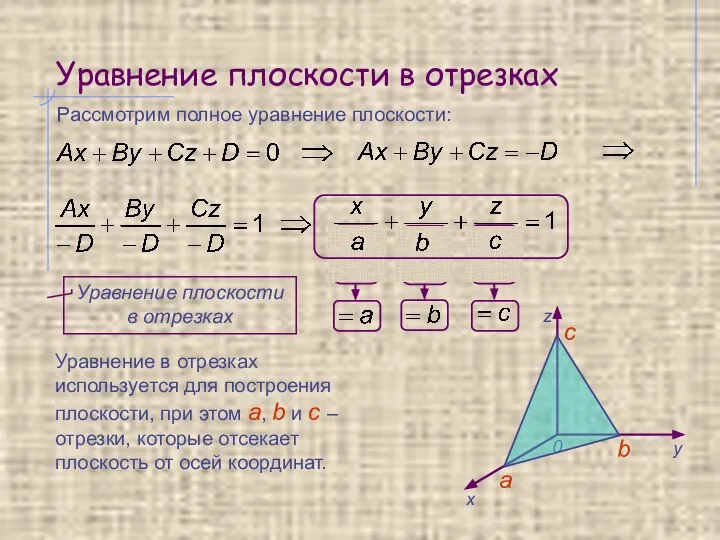
Уравнение плоскости в отрезках
Рассмотрим полное уравнение плоскости:
Уравнение в отрезках используется для построения плоскости, при этом a, b и с – отрезки, которые отсекает плоскость от осей координат.
Уравнение плоскости в отрезках
a
b
с

Уравнение плоскости, проходящей через три точки
Пусть точки М1(х1 ; у1 ; z1 ), М2(х2 ; у2 ; z2 ) и М3(х3 ; у3 ; z3 ) не лежат на одной прямой.
Тогда векторы:
и
не коллинеарны.
М1
М2
М3
М
Точка М(х ; у ; z ) лежит в одной плоскости с точками М1 , М2 и М3 только в том случае, если векторы:
и
компланарны.
Уравнение плоскости, проходящей через 3 точки

Угол между двумя плоскостями
Пусть две плоскости заданы общими уравнениями:
Углом между этими плоскостями называется угол между нормальными векторами к этим плоскостям.

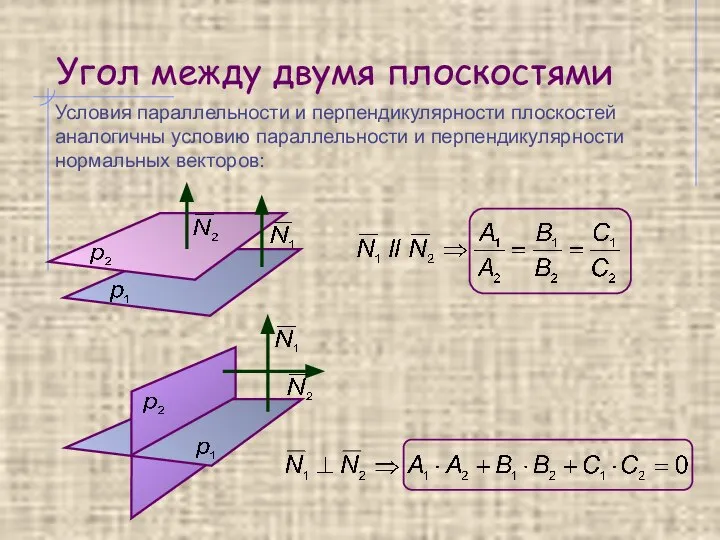
Угол между двумя плоскостями
Условия параллельности и перпендикулярности плоскостей аналогичны условию параллельности и перпендикулярности нормальных векторов:

Расстояние от точки до плоскости
Пусть точка М1(x1; y1; z1) – основание перпендикуляра, опущенного из точки М0(x0; y0; z0) на плоскость
М1
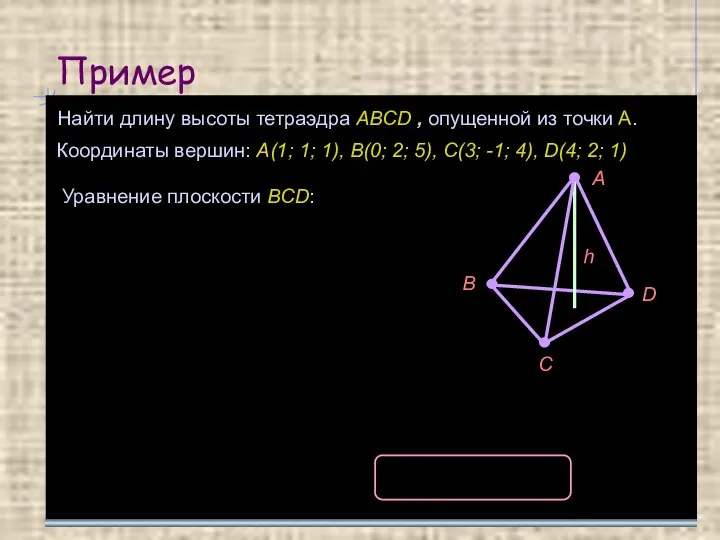
М0

Пример
Найти длину высоты тетраэдра ABCD , опущенной из точки A.
Координаты вершин: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2; 1)
Уравнение плоскости BCD:
A
B
С
D
h