Содержание
- 2. Тупиковая ДНФ Отношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия.
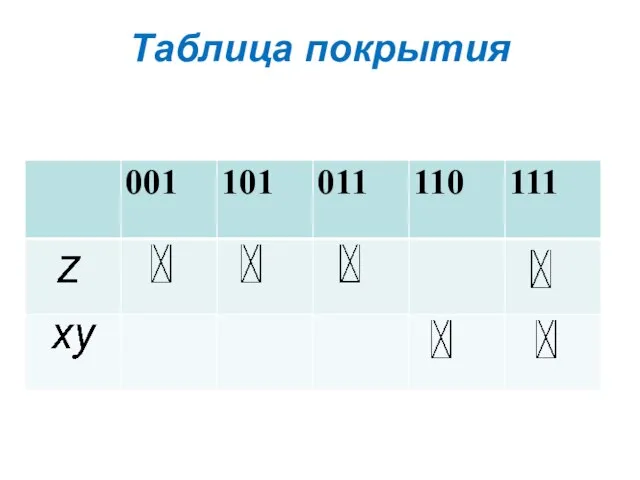
- 3. Таблица покрытия Строки таблицы соответствуют конъюнкциям ДНФ, столбцы – элементам единичного множества. На пересечении строки и
- 4. Пример Пусть ДНФ функции имеет вид: Тогда ее единичное множество может быть представлено в виде: Построим
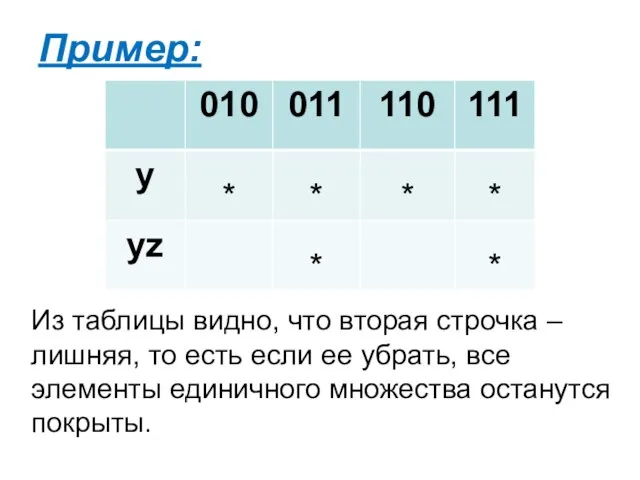
- 5. Пример: Из таблицы видно, что вторая строчка – лишняя, то есть если ее убрать, все элементы
- 6. Значит, импликант yz – лишний импликант. Пример Таким образом, ДНФ можно упростить, убрав лишний импликант. Эта
- 7. Тупиковая ДНФ Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой.
- 8. Замечание 1 Чтобы с помощью таблицы покрытия получить тупиковую ДНФ, необходимо сначала получить сокращенную ДНФ (скрДНФ)
- 9. Замечание 2 У функции может быть несколько тупиковых ДНФ. Чтобы найти их необходимо построить сокращенную ДНФ,
- 10. Метод Блейка-Порецкого – метод получения сокращенной ДНФ, содержащей все простые импликанты. Пусть дана СДНФ функции. 1.
- 11. Метод Блейка-Порецкого 3. Допишем к списку полученных конъюнкций те, которые не участвовали в склеивании (их номера
- 12. Пример 1 Дана СДНФ вида: Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
- 13. Метод Блейка-Порецкого П. 1. ; П. 2, 3. ; П.4 .
- 14. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-Порецкого Построим таблицу покрытия:
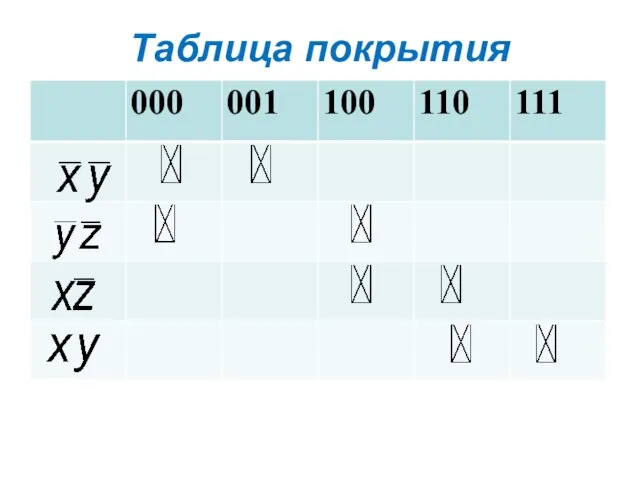
- 15. Таблица покрытия
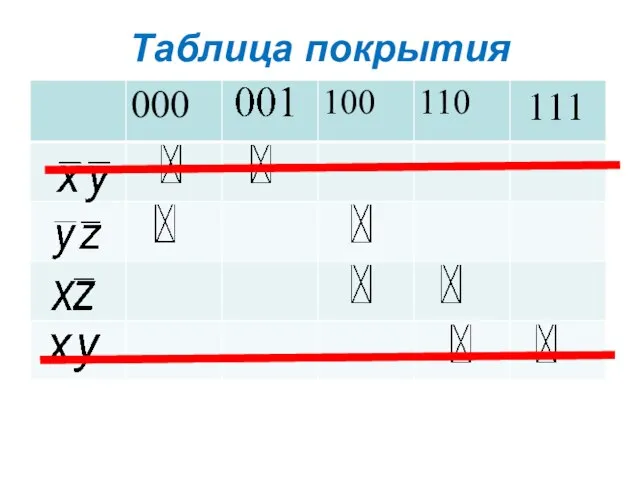
- 16. Таблица покрытия
- 17. Таблица покрытия
- 18. Таблица покрытия
- 19. Пример 2 Дана СДНФ вида: Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
- 20. Метод Блейка-Порецкого П. 1. П. 2, 3. П.4.
- 21. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-Порецкого Построим таблицу покрытия:
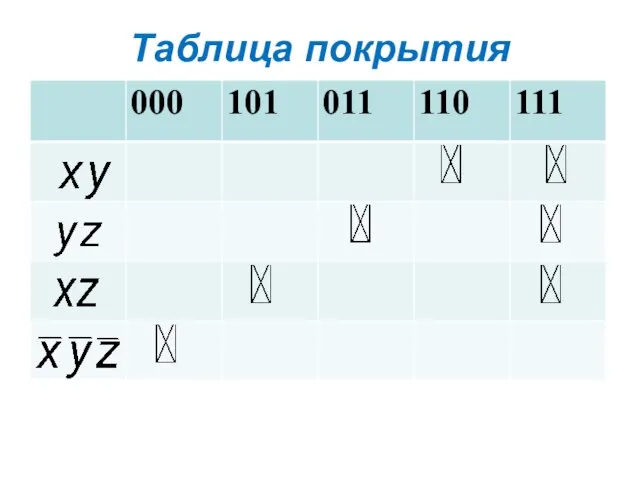
- 22. Таблица покрытия
- 23. Таблица покрытия
- 24. Пример 3 Дана СДНФ вида: Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.
- 25. Метод Блейка-Порецкого П. 1. П. 2, 3. П.4. l
- 26. Метод Блейка-Порецкого П. 1. П. 2, 3. П.4. l
- 27. Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Метод Блейка-Порецкого Построим таблицу покрытия:
- 28. Таблица покрытия
- 30. Скачать презентацию






















 Человек и число
Человек и число Презентация на тему Обыкновенные дроби
Презентация на тему Обыкновенные дроби  Прямые. Преобразование чертежа прямой. Две прямые
Прямые. Преобразование чертежа прямой. Две прямые Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша) Смысл умножения. Тренажер
Смысл умножения. Тренажер Скалярное произведение векторов
Скалярное произведение векторов Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику Решаем задачи на логику. Занятие 5
Решаем задачи на логику. Занятие 5 Вычисление объемов многогранников
Вычисление объемов многогранников Золотое сечение в архитектуре
Золотое сечение в архитектуре Дискретные случайные величины
Дискретные случайные величины Формулы приведения
Формулы приведения Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции
Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции Площадь круга и секторов
Площадь круга и секторов Перпендикулярность прямых, прямой и плоскости
Перпендикулярность прямых, прямой и плоскости Первообразная и интеграл
Первообразная и интеграл Связь между компонентами и результатом умножения. Чётные и нечётные числа
Связь между компонентами и результатом умножения. Чётные и нечётные числа Логика действий
Логика действий Сложение и вычитание десятичных дробей. Электронный урок
Сложение и вычитание десятичных дробей. Электронный урок Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Подготовка к ГИА. Модуль Геометрия
Подготовка к ГИА. Модуль Геометрия Интеграл
Интеграл Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Планиметрия. От углов до многоугольников. Повторение материала
Планиметрия. От углов до многоугольников. Повторение материала Правильные многогранники
Правильные многогранники Устная работа
Устная работа Пирамида. Применение логических законов в решении логических содержательных задач
Пирамида. Применение логических законов в решении логических содержательных задач Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ
Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ