Углы треугольника

Повторение (подсказка)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
Если треугольники подобны, то высоты, проведенные к сходственным сторонам, пропорциональны.

Повторение (2)
Найти расстояние от проектора С до экрана В.
А
В
180 см
90 см
240 см
С
H₁
H
Луч проектора АН₁⍊ экранам А и В.
∆CAE и ∆СВF подобны по двум углам (∠С общий, ∠САЕ=
∠ABF как соответственные при АЕ ⃦BF и секущей СВ).
F
Е
⇒
⇒

Повторение (подсказка)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
Если треугольники подобны, то сходственные стороны пропорциональны.

Повторение (2)
Человек ростом 1,7м стоит на некотором расстоянии от столба, на котором висит фонарь на высоте 5,1м, при этом длина его тени – 10м. Найдите расстояние от человека до фонаря (в метрах).
E
C
D
B
А
∆АВC и ∆ADF подобны по двум углам (∠A - общий, ∠СAB=
=∠ADF=90⁰).
⇒
Стороны ВC и DF – сходственные.
Так как DF=3ВС,
то АD=3АВ=3∙10=30м.

Повторение (подсказка)
Сумма острых углов прямоугольного треугольника равна 90⁰
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то треугольники равны
В равных треугольниках соответственные стороны равны

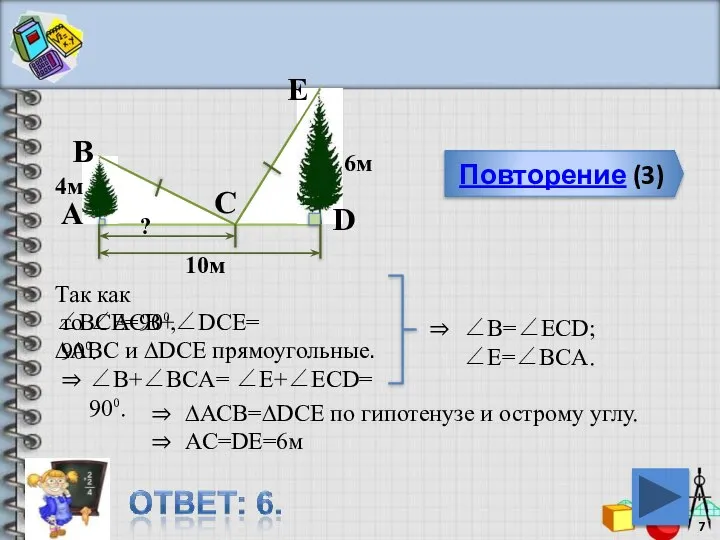
Повторение (3)
E
C
D
B
А
4м
?
6м
10м
Так как ∠ВСЕ=90⁰,
∆АВC и ∆DСЕ прямоугольные.
⇒
то ∠АСВ+∠DCE= 90⁰.
∠В+∠ВCА= ∠Е+∠ЕCD= 90⁰.
⇒
∠В=∠ЕCD; ∠Е=∠ВCА.
⇒
∆АСВ=∆DCE по гипотенузе и острому углу.
⇒
АС=DE=6м

Повторение (подсказка)
Если отрезок разделен на части, то его длина равна сумме длин частей отрезка.

Повторение (1)
48м
18м
?
1) 48 – 18 = 30 (м) расстояние между крайними столбами.
2) 30 : 2 = 15 (м) расстояние соседними столбами.
3) 18 + 15 = 33(м) расстояние между средним столбом и
дорогой.

Повторение (подсказка)
Прямоугольным называется треугольник, у которого есть прямой угол.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Повторение (2)
Лестница длиной 12,5 м приставлена к стене так, что расстояние от ее нижнего конца до стены равно 3,5 м. На какой высоте от земли находится верхний конец лестницы?
Ответ дайте в метрах.
С
В
А
∆АВС – прямоугольный,
⇒
по теореме Пифагора
3,5м
12,5м

Повторение (подсказка)
Площадь прямоугольника равна произведению длины на ширину.

Повторение (2)
Длина футбольного поля в форме прямоугольника в 1,5 раза больше ширины. Sполя = 7350м². Найдите ширину поля.
Пусть х м – ширина поля,
тогда 1,5х м – длина поля,
х ∙ 1,5х = 7350
х² = 7350 : 1,5
х₂ = -70
х₁ = 70;
Корень уравнения х₂ = -70 не удовлетворяет условию задачи.
b
а

Повторение (подсказка)
Объем прямоугольного параллелепипеда равен произведению его измерений. V=a*b*c
Если одна величина больше другой в n раз, то другая величина в n раз меньше первой.

Повторение (2)
Длина гаража в 2 раза больше его ширины и в 3 раза больше его высоты. Объем гаража равен 121,5 м³. Найдите высоту гаража.
C
B
А
D
Гараж имеет форму прямоугольного параллелепипеда,
⇒
где х м – длина гаража,
⇒
х = 9,
⇒
9м – длина гаража,
3м – высота гаража.

Повторение (подсказка)
Круг составляет 360⁰