Содержание
- 3. Умножим тройку на число α: Не является подпространством векторного пространства. 2. Проверим свойство умножения на число.
- 4. 4. Проверим свойства умножения на число и суммы двух векторов: Является подпространством векторного пространства. 5. Проверим
- 5. Тест 2-4. Задача № 2 См. лекцию 2.4.5 Пересечение и сумма подпространств. Часть 1
- 6. Тест 2-4. Задача № 3 См. лекцию 2.4.6 Пересечение и сумма подпространств. Часть 2
- 7. Тест 2-4. Задача № 4 -1 Проекция вектора на вектор в матричном виде выглядит как: (
- 8. Тест 2-4. Задача № 4 -2 Проекция вектора на вектор в матричном виде выглядит как: (
- 9. Нам известно, что: ( Лекция 2.4.4 Проецирование вектора на подпространство. Часть 2) Найдем матрицу проецирования М:
- 11. Тест 2-4. Задача 6.
- 12. Способ № 1 Будем минимизировать функцию: Составляем систему двух уравнений с двумя неизвестными: Тест 2-4. Задача
- 14. Способ № 2. Лекция 2.4.8 Примеры проецирования. МНК Составим нормальную систему уравнений (см. лекцию 2.4.4., 2.4.6):
- 15. Нормальная система уравнений :
- 16. Система в матричной форме записывается как: Где Тест 2-4. Задача 8.
- 17. Составим нормальную систему уравнений:
- 18. В результате умножения двух векторов, получается вектор, перпендикулярный перемножаемым векторам. Воспользуемся этим свойством. Найдем векторное произведение
- 20. Скачать презентацию








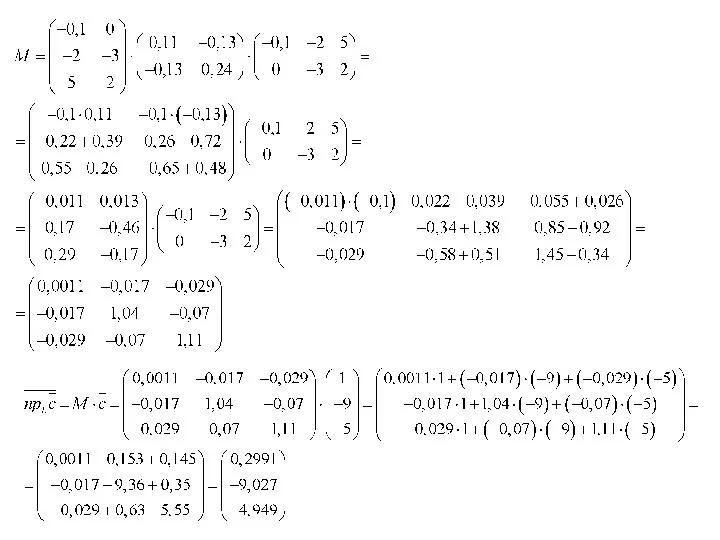








 Смешанные числа (часть 1)
Смешанные числа (часть 1) Математика. Лекция
Математика. Лекция Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Способы задания функции
Способы задания функции Четные и нечетные функции. Периодичность функций
Четные и нечетные функции. Периодичность функций Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Презентация на тему МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ  К уроку математики
К уроку математики Теория принятия решений. Вопросы к экзамену
Теория принятия решений. Вопросы к экзамену Reshenie_sistem_logicheskikh_uravneniy_vse_metody
Reshenie_sistem_logicheskikh_uravneniy_vse_metody Умножение 7, 8, 9, 10 (Закрепление)
Умножение 7, 8, 9, 10 (Закрепление) Перетворення подібності. Гомотерапія
Перетворення подібності. Гомотерапія Числа второго десятка
Числа второго десятка Квадратные уравнения и знаки его корней
Квадратные уравнения и знаки его корней Задачи по стереометрии. Подготовка к ЕГЭ
Задачи по стереометрии. Подготовка к ЕГЭ ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Обыкновенные дифференциальные уравнения. (Лекция 5)
Обыкновенные дифференциальные уравнения. (Лекция 5) Сечения, их назначение и применение
Сечения, их назначение и применение Площадь криволинейной трапеции с помощью интеграла
Площадь криволинейной трапеции с помощью интеграла Двойственные задачи линейного программирования. Лекция 3
Двойственные задачи линейного программирования. Лекция 3 Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода Урок - путешествие. Математика (1 класс)
Урок - путешествие. Математика (1 класс) Презентация на тему Статистика
Презентация на тему Статистика  Укрупненные единицы счета
Укрупненные единицы счета Средние величины. (Лекция 4.1)
Средние величины. (Лекция 4.1) Многоугольники. 9 класс
Многоугольники. 9 класс Число Пи вокруг нас
Число Пи вокруг нас Подготовка к контрольной работе
Подготовка к контрольной работе Формирование и развитие познавательных УУД на уроках математики
Формирование и развитие познавательных УУД на уроках математики