Сфера. Окружность и круг

План презентации
Определение сферы, шара.
Уравнение сферы.
Взаимное расположение сферы и плоскости.
Площадь сферы.
Итог урока.
Опр.окр.

Окружность и круг
Часть плоскости, ограниченная окружностью, называется кругом.
Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точки.
r – радиус;
d – диаметр
Опр. сферы

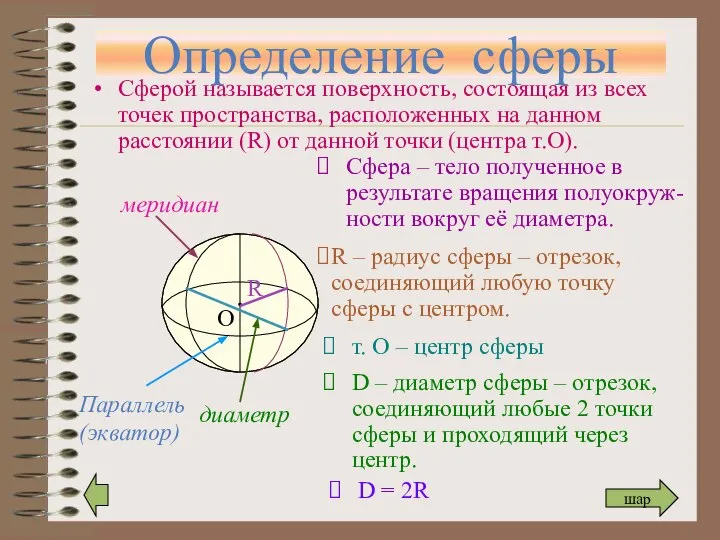
Определение сферы
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от данной точки (центра т.О).
Сфера – тело полученное в результате вращения полуокруж-ности вокруг её диаметра.
т. О – центр сферы
О
D – диаметр сферы – отрезок, соединяющий любые 2 точки сферы и проходящий через центр.
D = 2R
шар
R – радиус сферы – отрезок, соединяющий любую точку сферы с центром.

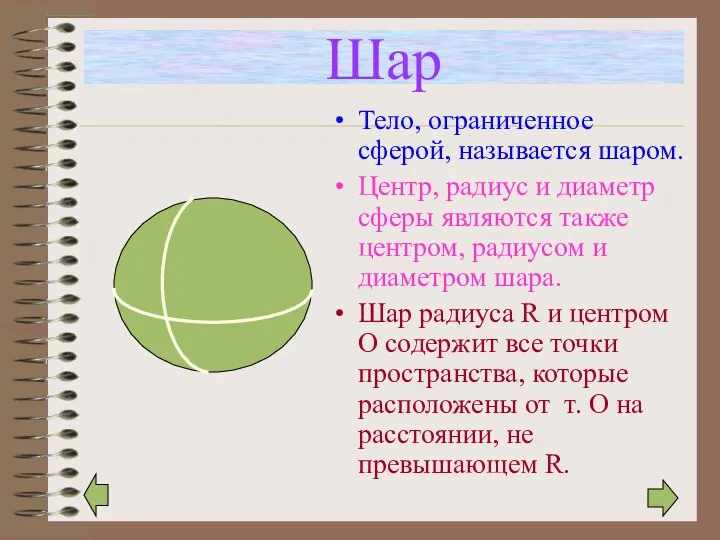
Шар
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара.
Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.

Исторические сведения о сфере и шаре
Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» - мяч.
В древности сфера и шар были в большом почёте. Астрономические наблюдения над небесным сводом вызывали образ сферы.
Пифагорейцы в своих полумистических рассуждениях утверждали, что сферические небесные тела располагаются друг от друга на расстоянии пропорциональном интервалам музыкальной гаммы. В этом усматривались элементы мировой гармонии. Отсюда пошло выражение «музыка сферы».
Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер.
Сфера, шар всегда широко применялись в различных областях науки и техники.
д/з прим.

Как изобразить сферу?
R
1. Отметить центр сферы (т.О)
2. Начертить окружность с центром в т.О
3. Изобразить видимую вертикальную дугу (меридиан)
4. Изобразить невидимую вертикальную дугу
5. Изобразить видимую гори-зонтальную дугу (параллель)
6. Изобразить невидимую горизонтальную дугу
7. Провести радиус сферы R
О
ур. окр.

Уравнение окружности
С(х0;у0)
М(х;у)
х
у
О
следовательно уравнение
окружности имеет вид:
(x – x0)2 + (y – y0)2 = r2
Зададим прямоугольную систему координат Оxy
Построим окружность c центром в т. С и радиусом r
Расстояние от произвольной т. М (х;у) до т.С вычисляется по формуле:
МС = (x – x0)2 + (y – y0)2
МС = r , или МС2 = r2

Задача 1.
Зная координаты центра С(2;-3;0), и радиус сферы R=5, записать уравнение сферы.
Решение
так, как уравнение сферы с радиусом R и центром в точке С(х0;у0;z0) имеет вид (х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы (x-2)2 + (y+3)2 + z2=25
Ответ: (x-2)2 + (y+3)2 + z2=25
ур. сферы

Уравнение сферы
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2
х
у
z
М(х;у;z)
R
Зададим прямоугольную систему координат Оxyz
Построим сферу c центром в т. С и радиусом R
МС = (x – x0)2 + (y – y0)2 + (z – z0)2
МС = R , или МС2 = R2
C(x0;y0;z0)
следовательно уравнение
сферы имеет вид:

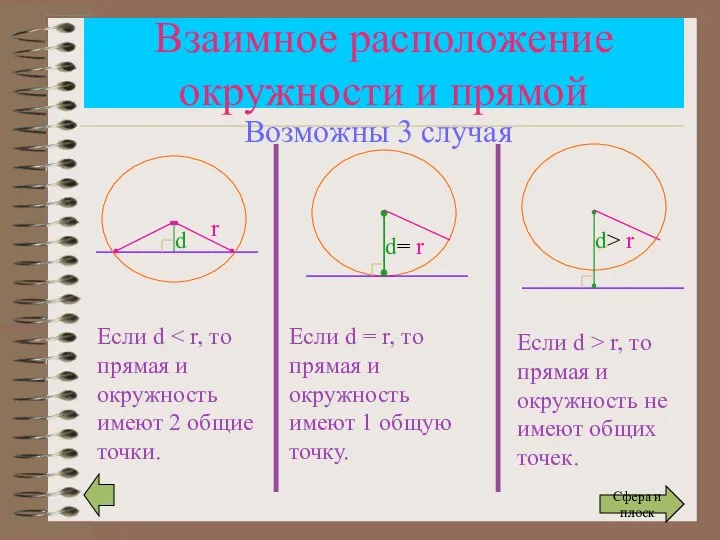
Взаимное расположение окружности и прямой
r
d
Если d < r, то прямая и окружность имеют 2 общие точки.
d= r
d> r
Если d = r, то прямая и окружность имеют 1 общую точку.
Если d > r, то прямая и окружность не имеют общих точек.
Возможны 3 случая
Сфера и плоск

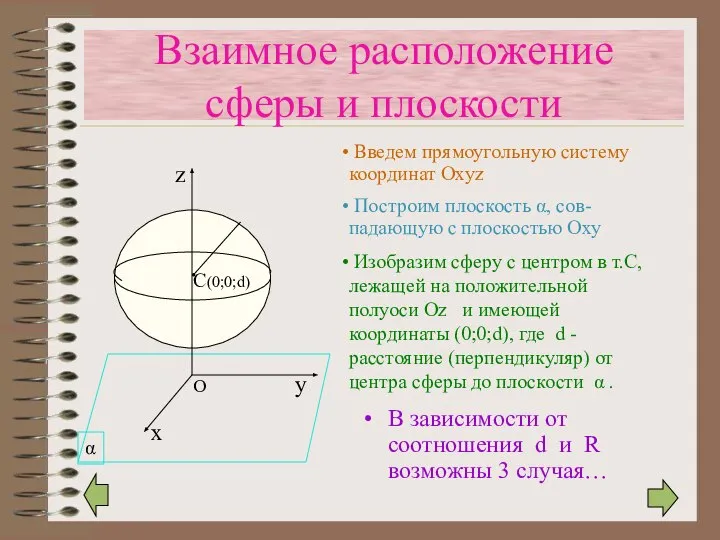
Взаимное расположение сферы и плоскости
В зависимости от соотношения d и R возможны 3 случая…
Введем прямоугольную систему координат Oxyz
Построим плоскость α, сов-падающую с плоскостью Оху
Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d - расстояние (перпендикуляр) от центра сферы до плоскости α .

Сечение шара плоскостью есть круг.
r
Взаимное расположение сферы и плоскости
Рассмотрим 1 случай
d < R, т.е. если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность радиусом r.
r = R2 - d2
М
С приближением секущей плоскости к центру шара радиус круга увеличивается. Плоскость, проходящая через диаметр шара, называется диаметральной. Круг, полученный в результате сечения, называется большим кругом.

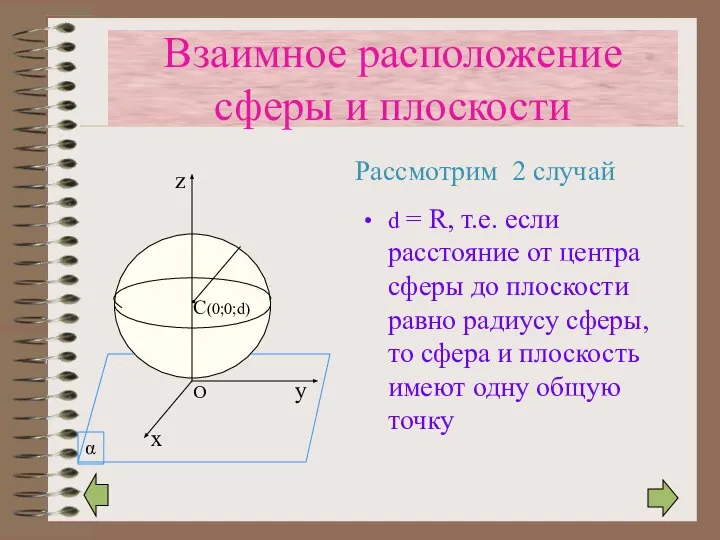
d = R, т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют одну общую точку
Взаимное расположение сферы и плоскости
Рассмотрим 2 случай

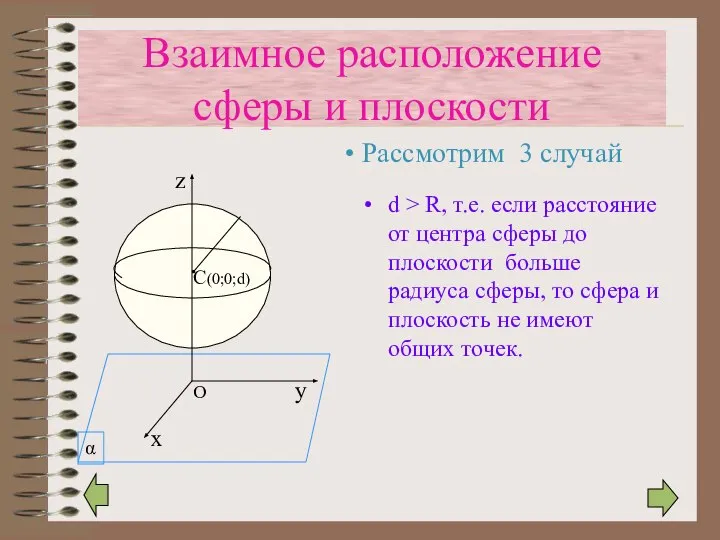
d > R, т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.
Взаимное расположение сферы и плоскости
Рассмотрим 3 случай

Задача 2.
Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти радиус сечения.
Дано:
Шар с центром в т.О
R=41 дм
α - секущая плоскость
d = 9 дм
Найти: rсеч = ?
Решение:
Рассмотрим ∆ОМК – прямоугольный
ОМ = 41 дм; ОК = 9 дм; МК = r, r = R2 - d2
по теореме Пифагора: МК2 = r2 = 412- 92 = 1681 - 81=1600 отсюда rсеч = 40 дм
Ответ: rсеч = 40 дм
r

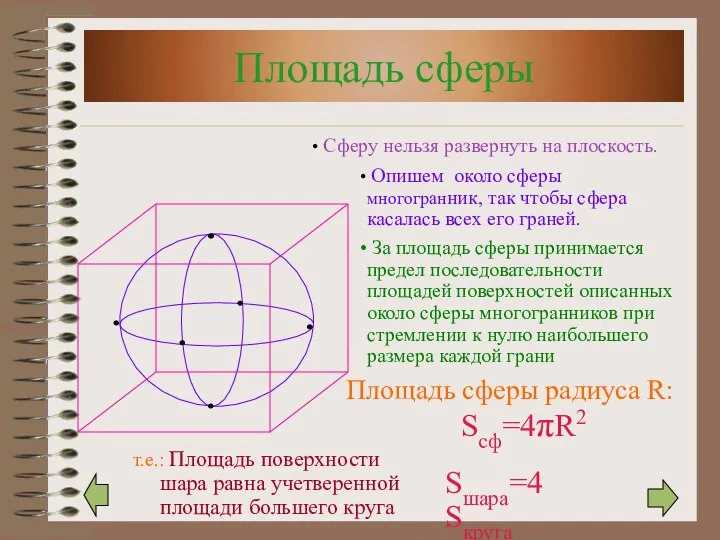
Площадь сферы
Площадь сферы радиуса R: Sсф=4πR2
Сферу нельзя развернуть на плоскость.
Опишем около сферы многогранник, так чтобы сфера касалась всех его граней.
За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани
т.е.: Площадь поверхности шара равна учетверенной площади большего круга
Sшара=4 Sкруга

Задача 3.
Найти площадь поверхности сферы,
радиус которой = 6 см.
Дано:
сфера
R = 6 см
Найти:
Sсф = ?
Решение:
Sсф = 4πR2
Sсф = 4π 62 = 144π см2
Ответ: Sсф = 144π см2

Решите задачи по данной теме
Сфера, радиусом 15см, пересечена плоскостью, проходящей на расстоянии 9см от центра сферы. Найти длину линии пересечения сферы и плоскости.
Плоскость, касающаяся шара, проходит на расстоянии 4см от центра шара. Найти площадь поверхности шара.
Диаметр шара равен 6. Через конец диаметра проведена плоскость под углом 450 к нему. Найдите площадь сечения шара этой плоскостью.
Площадь сферы, вписанной в куб, равна 25π. Найти радиус сферы, описанной около этого куба.