Содержание
- 2. На практике часто проводятся серии экспериментов, независимых относительно некоторого события А. Это означает, что вероятность наступления
- 3. §1. Формула Бернулли Теорема. Вероятность того, что событие А наступит m раз в n независимых испытаниях
- 4. Пример 1 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=5
- 5. 5 Лекция 3. Повторные независимые испытания Якоб Бернулли (1655-1705) Формула Бернулли названа в честь её автора
- 6. Определение. Наивероятнейшим числом наступления события А в серии n независимых экспериментов называется число m0 для которого
- 7. Доказательство. 7 Лекция 3. Повторные независимые испытания §1. Формула Бернулли
- 8. Пример 2 8 Ответ: от 14 до 19 Лекция 3. Повторные независимые испытания Эксперимент: выбрать наугад
- 9. §2. Формула Пуассона Теорема. Если при неограниченном увеличении числа испытаний n вероятность р наступления события А
- 10. Доказательство. 10 Лекция 3. Повторные независимые испытания §2. Формула Пуассона
- 11. Пример 3 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=50
- 12. 12 Лекция 3. Повторные независимые испытания Симеон Дени Пуассон (1781-1840) В 1837 году была опубликована работа
- 13. §3. Локальная теорема Муавра-Лапласа Теорема. Если вероятность р наступления события А в каждом испытании постоянна, отлична
- 14. §3. Локальная теорема Муавра-Лапласа Свойства функции Гаусса : Замечание 1. Замечание 2. 14 Лекция 3. Повторные
- 15. Пример 4 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=200
- 16. 16 Лекция 3. Повторные независимые испытания Абрахам де Муавр (1667-1754) Английский математик французского происхождения Абрахам де
- 17. 17 Лекция 3. Повторные независимые испытания Пьер Симон Лаплас (1749-1827) Большинство результатов де Муавра вскоре были
- 18. §4. Интегральная теорема Муавра-Лапласа Теорема. Если вероятность р наступления события А в каждом испытании постоянна, отлична
- 19. Свойства функции Лапласа : Замечание 1. Замечание 2. 19 Лекция 3. Повторные независимые испытания §4. Интегральная
- 20. Пример 5 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=200
- 21. Пример 5 21 Лекция 3. Повторные независимые испытания Ответ: ≈0,02%
- 22. §5. Следствия интегральной теоремы 22 Лекция 3. Повторные независимые испытания Следствие 1. Если вероятность р наступления
- 23. Пример 6 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=200
- 24. Пример 6 24 Лекция 3. Повторные независимые испытания Ответ: ≈0,08
- 25. 25 Лекция 3. Повторные независимые испытания Следствие 2. Если вероятность р наступления события А в каждом
- 26. Пример 7 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=200
- 27. Пример 7 27 Лекция 3. Повторные независимые испытания Ответ: ≈0,02%
- 28. 28 Лекция 3. Повторные независимые испытания Следствие 3. Если вероятность р наступления события А в каждом
- 29. Пример 8 Эксперимент: выбрать наугад деталь для проверки качества. Событие А : выбрана бракованная деталь. n=200
- 30. Пример 8 30 Лекция 3. Повторные независимые испытания Ответ: ≈100%
- 32. Скачать презентацию





























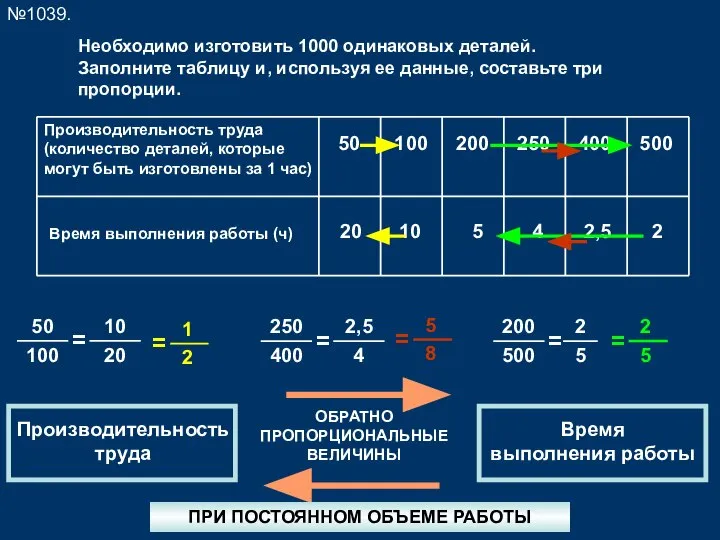 Пропорциональные величины
Пропорциональные величины Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Приближенные вычисления
Приближенные вычисления Решение тригонометрических уравнений
Решение тригонометрических уравнений Математический калейдоскоп
Математический калейдоскоп Таблица умножения на 3 в стихах
Таблица умножения на 3 в стихах Загадочное число
Загадочное число Решение уравнений. Математика. 6 класс
Решение уравнений. Математика. 6 класс Подготовка к ВПР
Подготовка к ВПР Путешествие по океану Математики
Путешествие по океану Математики Уравнения и неравенства. Решение систем неравенств
Уравнения и неравенства. Решение систем неравенств Пропорция – верное равенство двух отношений
Пропорция – верное равенство двух отношений Целые уравнения. Уравнения с модулем. ЕГЭ 11 - 1 Занятие 2
Целые уравнения. Уравнения с модулем. ЕГЭ 11 - 1 Занятие 2 Путешествие по морям
Путешествие по морям Презентация на тему ГИА 2013. Модуль «Алгебра» №7
Презентация на тему ГИА 2013. Модуль «Алгебра» №7  Симметрия многогранников
Симметрия многогранников Для чего мы изучаем геометрию?
Для чего мы изучаем геометрию? Квадратное уравнение
Квадратное уравнение Основные принципы комбинаторики
Основные принципы комбинаторики Линейные неравенства. Системы линейных неравенств. Повторение
Линейные неравенства. Системы линейных неравенств. Повторение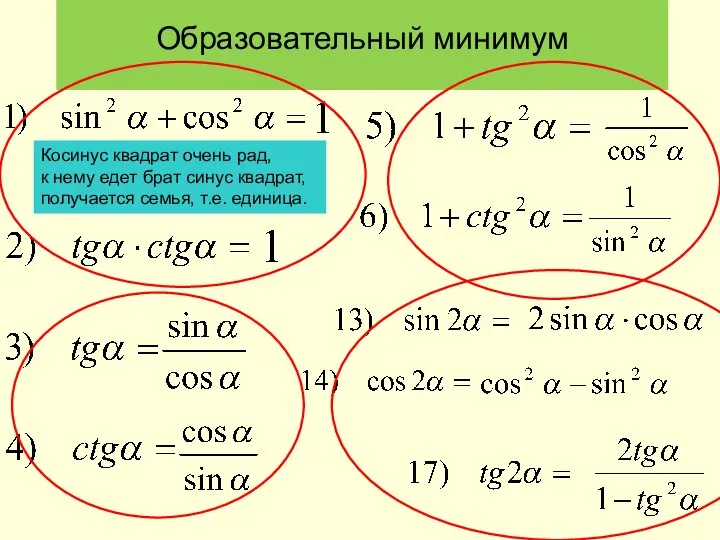 Образовательный минимум
Образовательный минимум Построение графиков функций
Построение графиков функций Практикум №5. Сквозной пример
Практикум №5. Сквозной пример Матричный метод решения СЛАУ
Матричный метод решения СЛАУ Симметрия. Виды симметрии
Симметрия. Виды симметрии Конус. Решение задач по готовым чертежам
Конус. Решение задач по готовым чертежам Теорема Пифагора
Теорема Пифагора Булева алгебра. Классы булевых функций
Булева алгебра. Классы булевых функций