Содержание
- 2. Определение двугранного угла Двугранным углом называется фигура, образованная двумя не принадлежащим одной плоскости полуплоскостями, имеющими общую
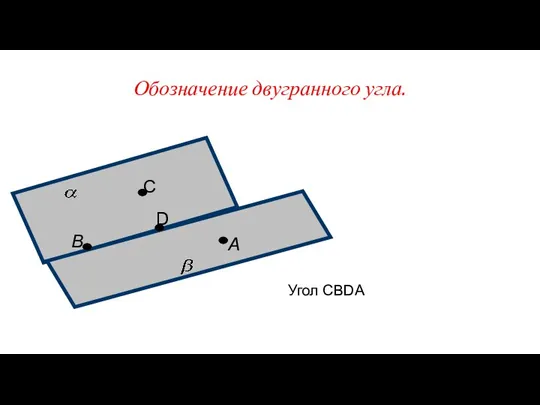
- 3. Обозначение двугранного угла. А В С D Угол CBDA
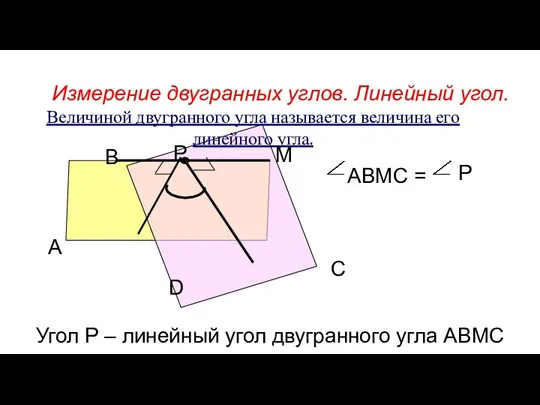
- 4. Измерение двугранных углов. Линейный угол. А В М D Р С АВМС = Р Угол Р
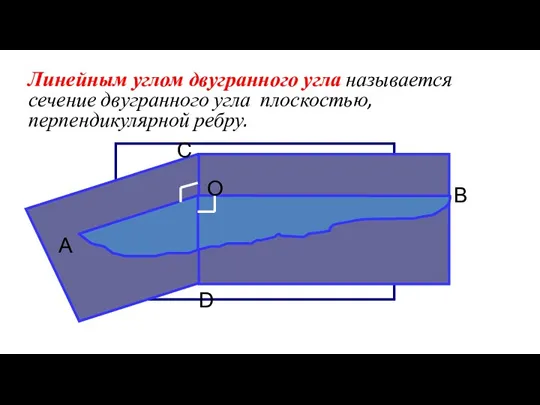
- 5. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 6. Способ нахождения (построения) линейного угла. 1. Найти ( увидеть) ребро и грани двугранного угла 2. В
- 7. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. A B O
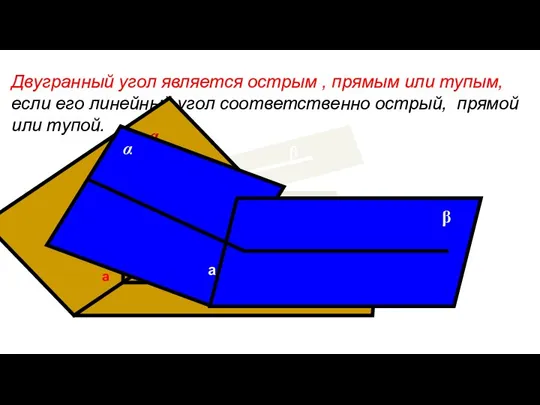
- 8. Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или
- 9. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
- 10. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении. Угол между
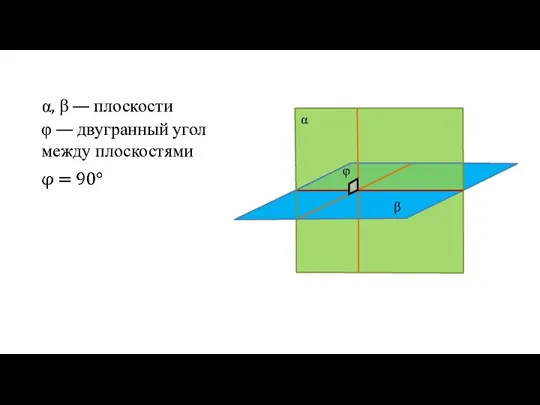
- 11. α, β — плоскости φ — двугранный угол между плоскостями α β φ
- 12. ε ⏊ σ, т.к. φ = 90° Определение Две плоскости называются перпендикулярными, если двугранный угол между
- 13. Стена и потолок
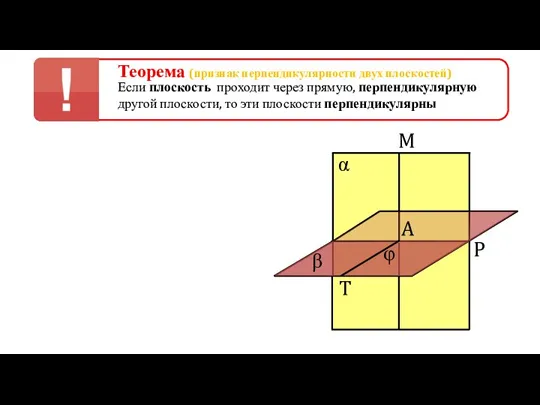
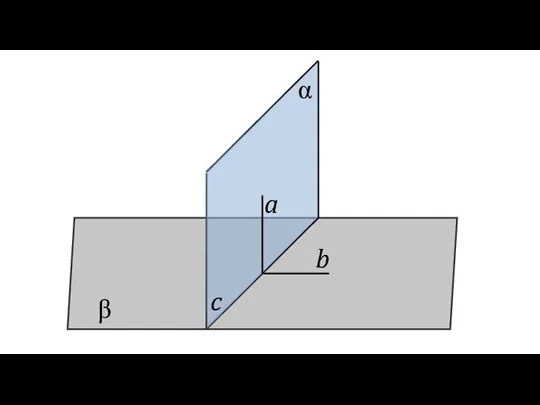
- 14. Теорема (признак перпендикулярности двух плоскостей) Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости
- 16. Дано: ΔАВС, ∠С = 90°, АС ⊂ α, ∠ между плоскостями α и △ABC = 60°,
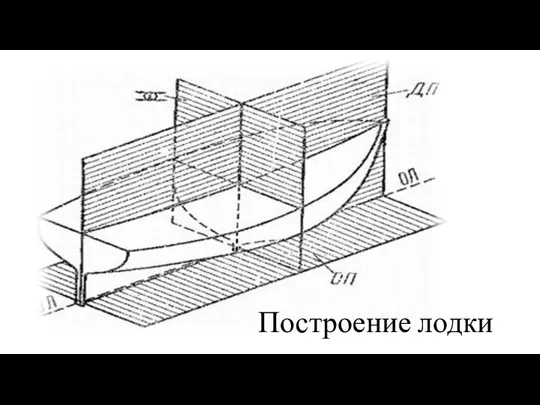
- 17. Построение лодки
- 18. Построение моста
- 19. Лестница
- 21. Скачать презентацию
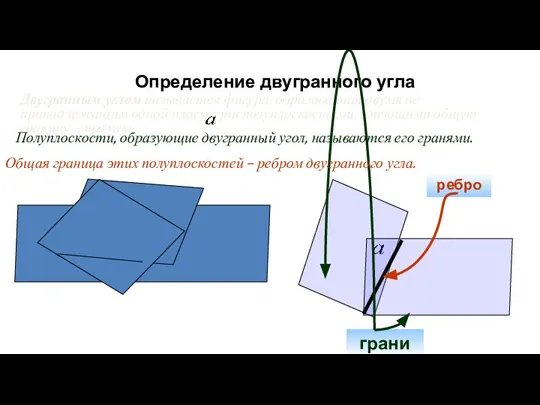









 Задачи на готовых чертежах по теме Подобие
Задачи на готовых чертежах по теме Подобие Тест по теме Цилиндр
Тест по теме Цилиндр Матрицы и определители
Матрицы и определители Математический калейдоскоп Областная интеллектуальная игра
Математический калейдоскоп Областная интеллектуальная игра Векторы. Нулевой вектор
Векторы. Нулевой вектор Сумма углов треугольника
Сумма углов треугольника Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств Квадратные неравенства
Квадратные неравенства Умножение числа 2 и на 2
Умножение числа 2 и на 2 Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Составление объемных фигур из отдельных элементов кубиков Сома
Составление объемных фигур из отдельных элементов кубиков Сома Размещения
Размещения Текстовые задачи. Часть 2. Понятие текстовой задачи и ее виды
Текстовые задачи. Часть 2. Понятие текстовой задачи и ее виды Системы уравнений. Основные понятия
Системы уравнений. Основные понятия Статистическая теория радиотехнических систем. Моменты случайных функций. (Лекция 3)
Статистическая теория радиотехнических систем. Моменты случайных функций. (Лекция 3) Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла
Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла Площади и объемы геометрических фигур
Площади и объемы геометрических фигур Подмножество. Операции над множествами. Самостоятельная работа
Подмножество. Операции над множествами. Самостоятельная работа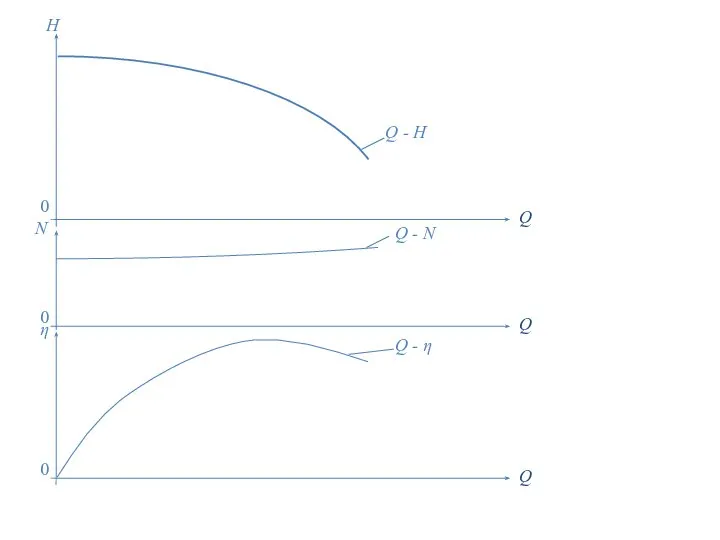 Закон пропорциональности
Закон пропорциональности Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Квадратные уравнения. Урок-путешествие
Квадратные уравнения. Урок-путешествие Введение в компьютерный и интеллектуальный анализ данных (ВКИАД)
Введение в компьютерный и интеллектуальный анализ данных (ВКИАД) Сериал Законы сложения
Сериал Законы сложения Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Ребусы от тётушки Совы
Ребусы от тётушки Совы Вычислительная математика. Практика №1
Вычислительная математика. Практика №1 Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 1