Содержание
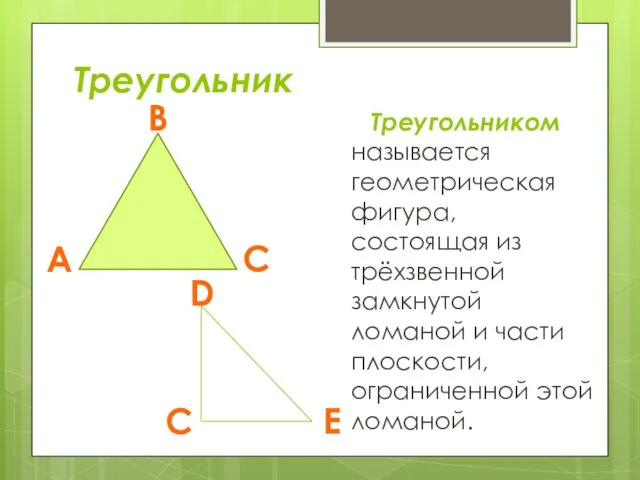
- 2. Треугольник Треугольником называется геометрическая фигура, состоящая из трёхзвенной замкнутой ломаной и части плоскости, ограниченной этой ломаной.
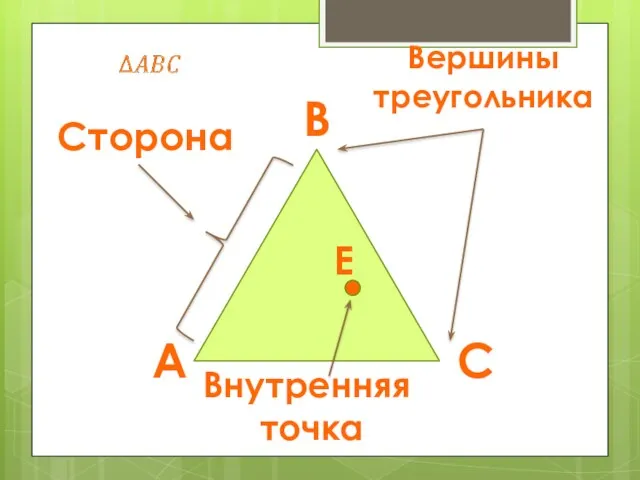
- 3. Вершины треугольника Сторона Внутренняя точка
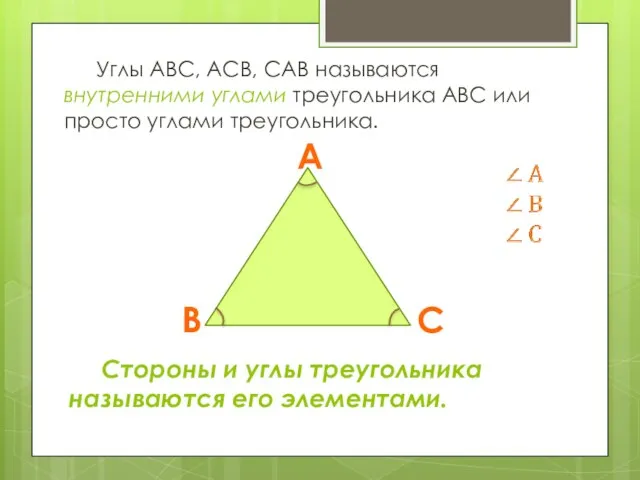
- 4. Углы АВС, АСВ, САВ называются внутренними углами треугольника АВС или просто углами треугольника. Стороны и углы
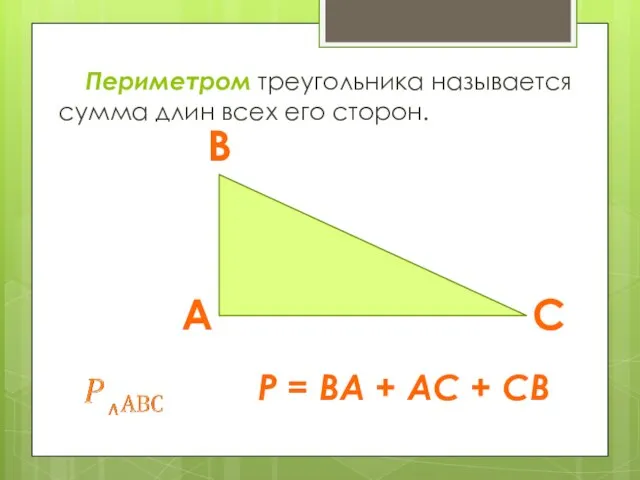
- 5. Периметром треугольника называется сумма длин всех его сторон. Р = ВА + АС + СВ
- 6. Два треугольника называются равными, если их можно совместить наложением, т.е. можно совместить их вершины, стороны и
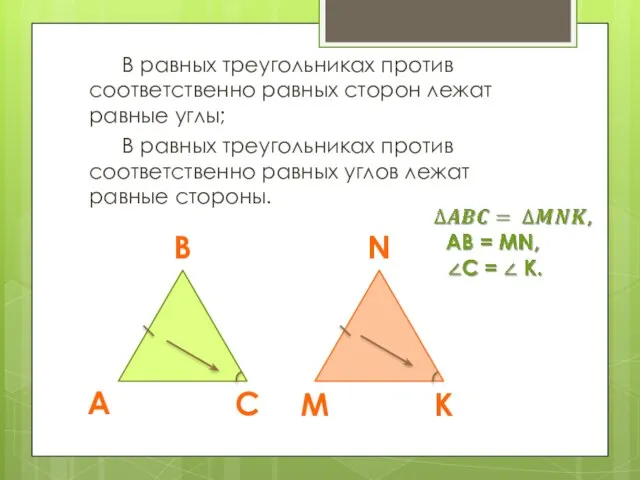
- 7. В равных треугольниках против соответственно равных сторон лежат равные углы; В равных треугольниках против соответственно равных
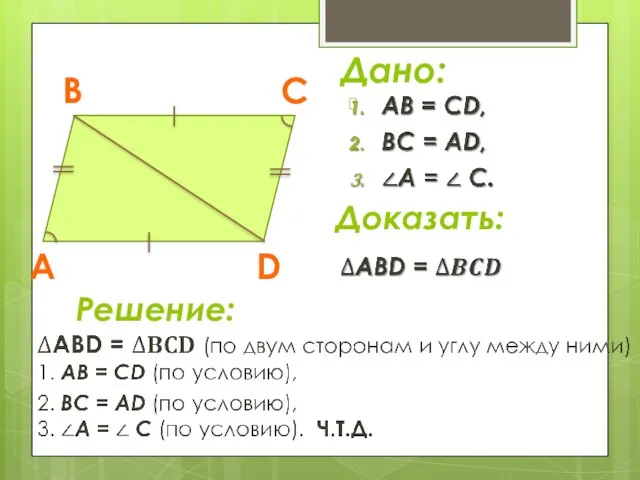
- 8. Теорема (первый признак равенства треугольников) Если две стороны и угол между ними одного треугольнику соответственно равны
- 10. Дано: Доказать:
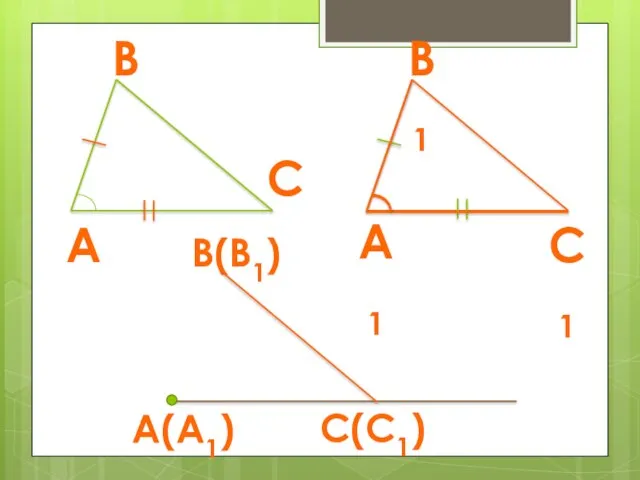
- 11. С(С1) В(В1)
- 12. Дано: Доказать: Решение:
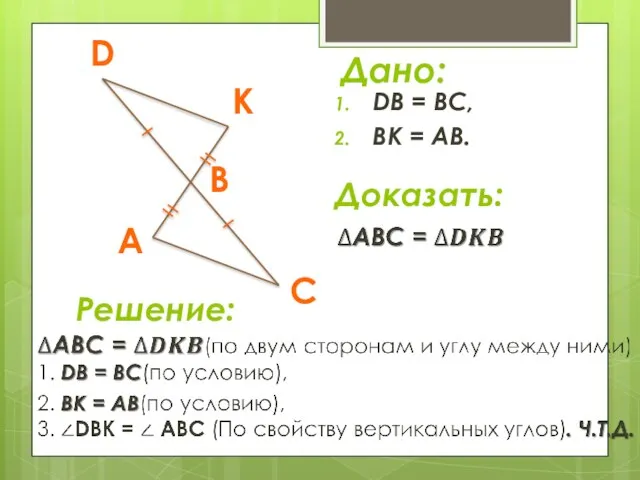
- 13. DB = BC, BK = AB. Дано: Доказать: Решение:
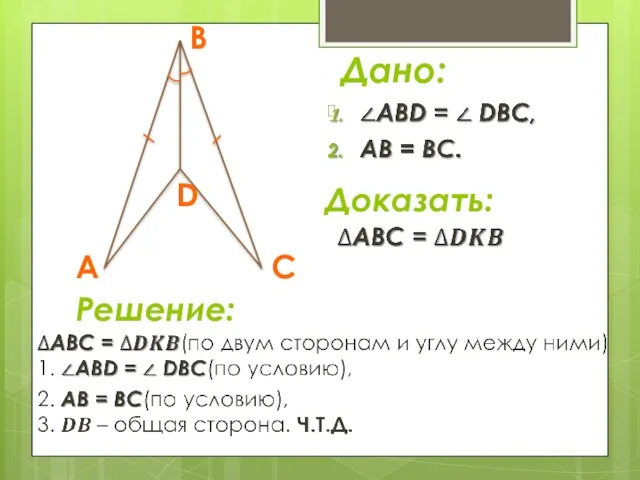
- 14. Доказать: Решение: Дано:
- 16. Скачать презентацию



 Основные понятия математической статистики. Лекция 6
Основные понятия математической статистики. Лекция 6 Музей по истории геометрии
Музей по истории геометрии Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного
Вычисление производной степенной функции. Правила дифференцирования. Производные суммы, разности, произведения, частного Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Презентация на тему Прямоугольная система координат
Презентация на тему Прямоугольная система координат  Графики функций. Задачи с параметрами
Графики функций. Задачи с параметрами Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Старинные меры веса 1 класс - Презентация по математике_
Старинные меры веса 1 класс - Презентация по математике_ Площадь поверхности цилиндра
Площадь поверхности цилиндра Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Уравнения! Реформа образования
Уравнения! Реформа образования Теорема Пифагора
Теорема Пифагора Фильтр Ходрика-Прескотта
Фильтр Ходрика-Прескотта Как умножали египтяне
Как умножали египтяне Фізико-математично-космічний конкурс
Фізико-математично-космічний конкурс Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел
Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел  Решение задач
Решение задач Понятие процента
Понятие процента Методы фильтрации контуров изображений
Методы фильтрации контуров изображений Булевы (гулевы) функции
Булевы (гулевы) функции Расчетное задание
Расчетное задание МатШах(0.1)
МатШах(0.1) Задачи с параметрами в заданиях Единого государственного экзамена
Задачи с параметрами в заданиях Единого государственного экзамена Сложение с переходом через десяток. Реши правильно примеры
Сложение с переходом через десяток. Реши правильно примеры Площадь фигур. Решение задач
Площадь фигур. Решение задач Теорема Пифагора и способы ее доказательства
Теорема Пифагора и способы ее доказательства