Содержание
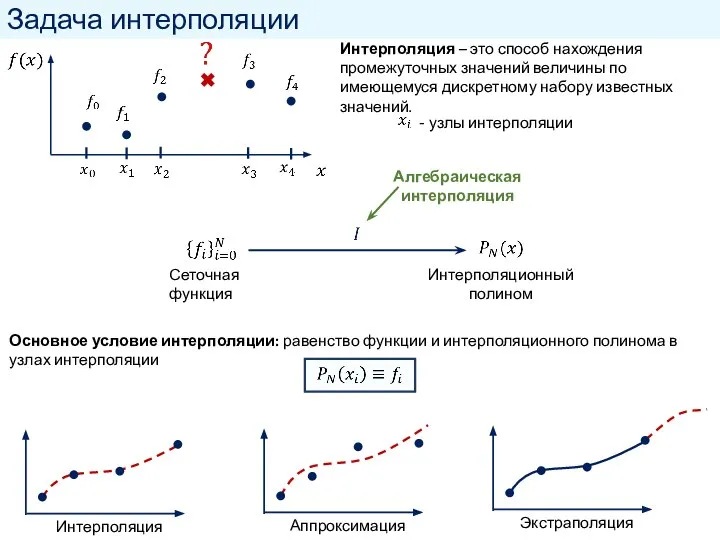
- 2. Задача интерполяции Интерполяция – это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
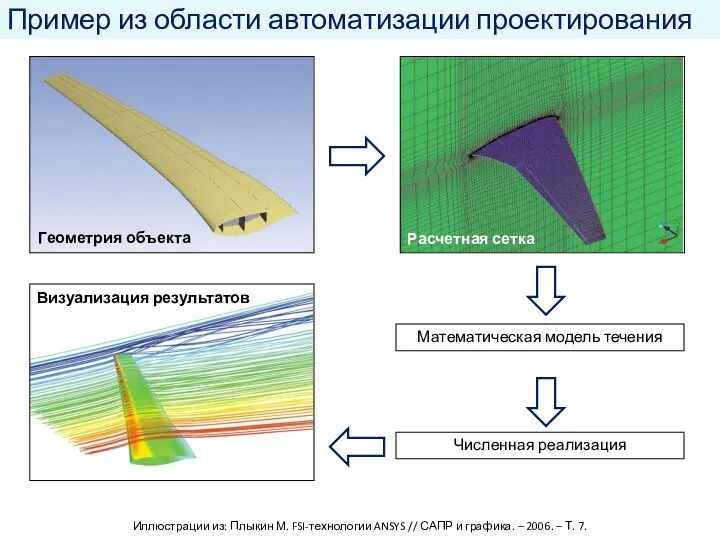
- 3. Пример из области автоматизации проектирования Математическая модель течения Численная реализация Геометрия объекта Расчетная сетка Визуализация результатов
- 4. Методы построения интерполяционного полинома
- 5. Интерполяция алгебраическими полиномами Определитель матрицы – детерминант Вандермонда. В случае различия всех узлов сетки он отличен
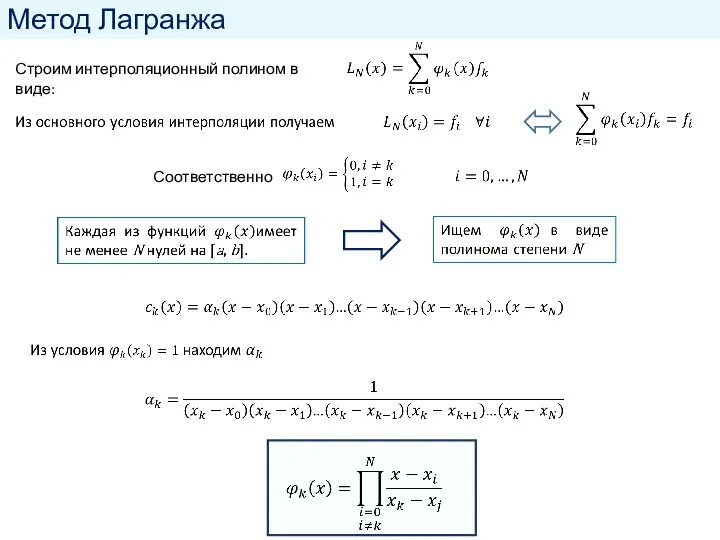
- 6. Метод Лагранжа
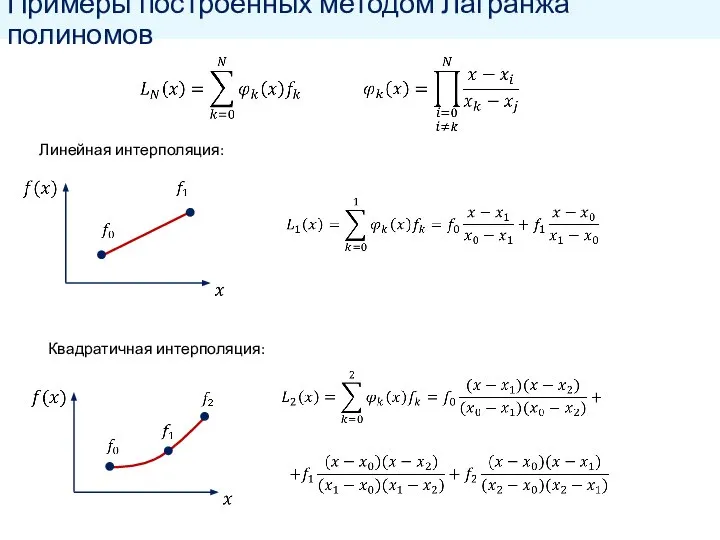
- 7. Примеры построенных методом Лагранжа полиномов
- 8. Метод Ньютона Разделенная разность первого порядка Разделенная разность второго порядка Интерполяционный полином в форме Ньютона Разделенная
- 9. Метод Ньютона Разделенная разность k-го порядка Интерполяционный полином в форме Ньютона
- 10. Примеры построенных методом Ньютона полиномов Добавка к P1(x)
- 11. Лагранж vs Ньютон Удобно применять, когда интерполируется одна и та же функция, но число узлов интерполяции
- 12. Погрешность интерполяции
- 13. Погрешность интерполяции Опр: Разница между функцией и интерполяционным полиномом N-ой степени в точке x называется остаточным
- 14. Погрешность интерполяции на равномерной сетке Утверждение 2.3. Для случая равномерной сетки на отрезке [a,b] для любого
- 15. Погрешность в задаче экстраполяции Экстраполяция – аппроксимация функции вне отрезка, на котором заданы узлы интерполяции. Экстраполяция
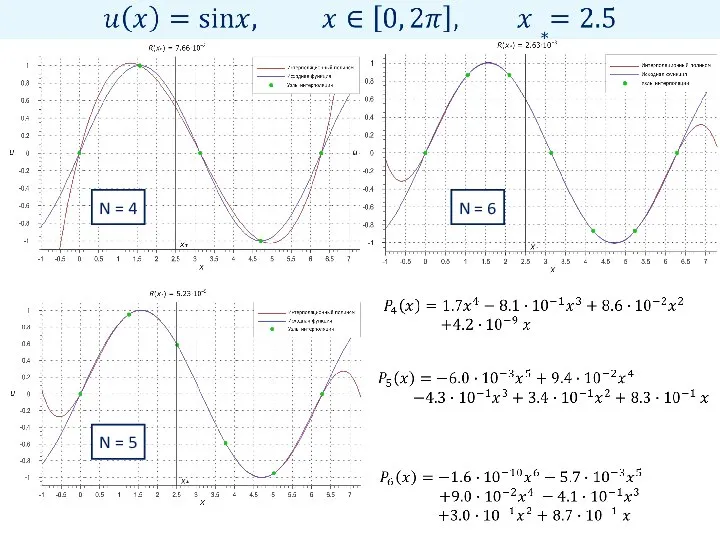
- 16. N = 4 N = 5 N = 6
- 17. Увеличение числа узлов интерполяции Сетка на [a, b]: Рассмотрим последовательность сеток с возрастающим числом узлов: Пусть
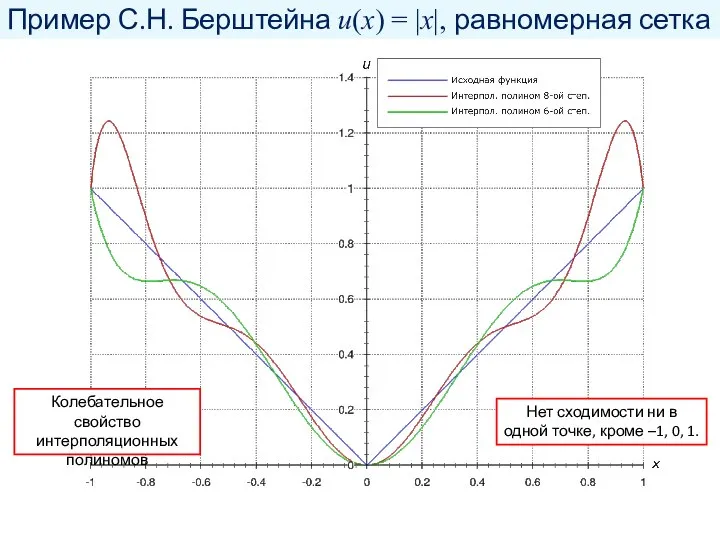
- 18. Пример С.Н. Берштейна u(x) = |x|, равномерная сетка Нет сходимости ни в одной точке, кроме –1,
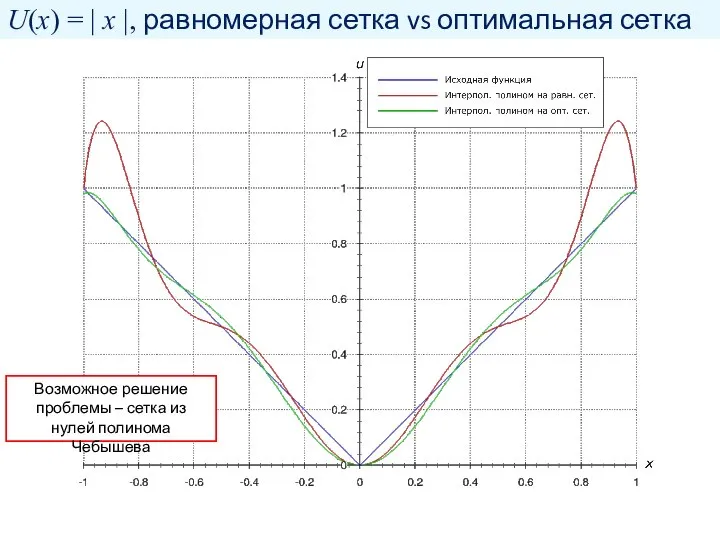
- 19. U(x) = | x |, равномерная сетка vs оптимальная сетка Возможное решение проблемы – сетка из
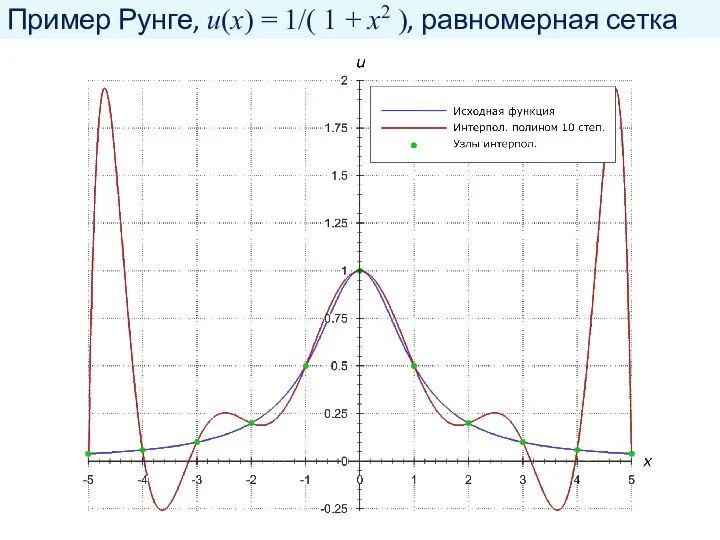
- 20. Пример Рунге, u(x) = 1/( 1 + x2 ), равномерная сетка
- 21. Влияние неустранимой погрешности Знаем как оценить Необходимо оценить Константа Лебега Пример. Константа Лебега для случая линейной
- 22. Интерполяция сплайнами
- 23. Недостатки глобальной интерполяции При вычислении многочлена высокой степени могут накапливаться ошибки округления (например как при суммировании
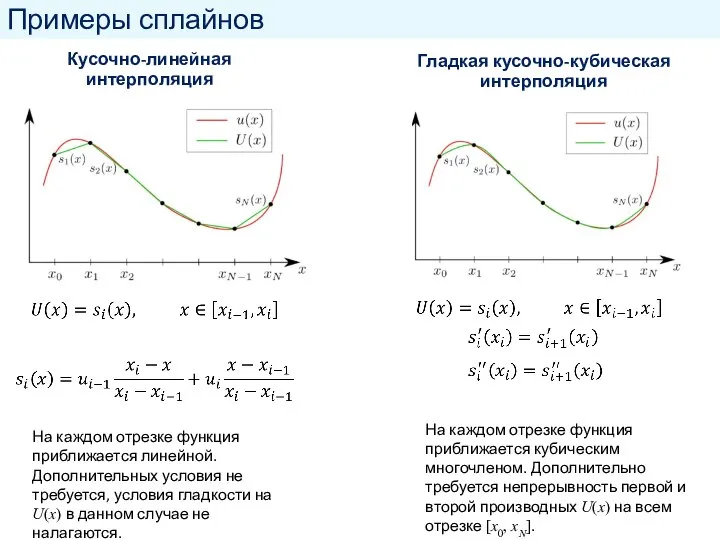
- 24. Примеры сплайнов На каждом отрезке функция приближается линейной. Дополнительных условия не требуется, условия гладкости на U(x)
- 25. Построение сплайна Характеристики сплайна Найдем выражения для функций si(x), составляющих гладкий кубический сплайн. Гладкостью сплайна называется
- 26. Построение сплайна Условия непрерывности Выпишем условия непрерывности первой и второй производной U(x) в точках xi-1: Условия
- 27. Построение сплайна Основное условия интерполяции Выпишем условия интерполирования, то есть U(xi) = u(xi): Кроме этого, есть
- 28. Система для нахождения сплайна В этой системе 3(N – 1) + N + 1 = 4N
- 29. Линейная система После добавления двух краевых условия количество уравнений совпало с количеством неизвестных. Можно было бы
- 30. Упрощение системы Подставим вместо ai значения u(xi): Из уравнения (3) и (7) выразим dihi: Исключим di
- 31. Упрощение системы После приведения подобных Выразим bi И подставим в уравнение (2’’) Заметим, что выражение для
- 32. Трехдиагональная система В результате серии упрощений у нас получилась система, относительно значений с1, … сN-1, причем,
- 33. Свойства сплайна Оказывается, что если u(x) непрерывна, то последовательность кубических сплайнов UN(x) будет сходиться к u(x)
- 34. Литература Петров И.Б., Лобанов А.И. Лекции по вычислительной математике: учеб. пособие. – М.: Интернет-Университет Информационных Технологий.
- 35. Спасибо за внимание!
- 36. Оптимальный выбор узлов интерполяции. Многочлены Чебышева.
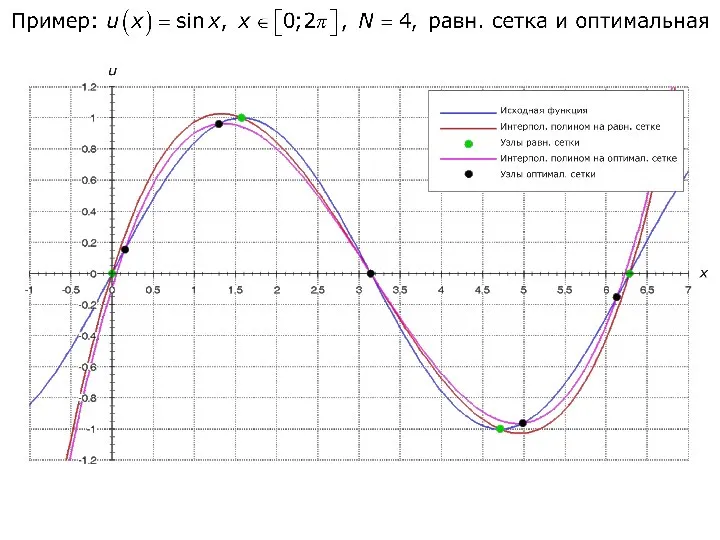
- 37. Минимизации погрешности интерполяции Минимизируем за счет выбора узлов интерполяции Получили задачу на минимакс (или задачу о
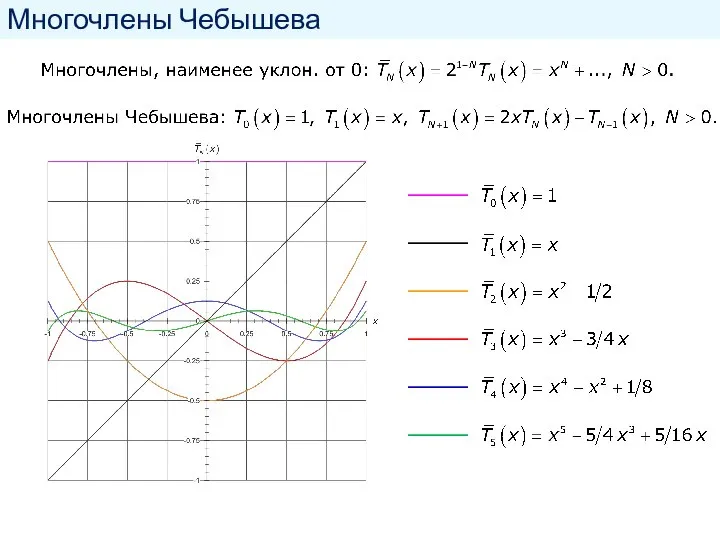
- 38. Многочлены Чебышева
- 39. Другая форма записи многочленов Чебышева Функция cos( N arccos x ) удовлетворяет тому же разностному уравнению,
- 40. Нули полиномов Чебышева Отрезок [–1,1] Отрезок [a,b]
- 43. Скачать презентацию










![Увеличение числа узлов интерполяции Сетка на [a, b]: Рассмотрим последовательность сеток с](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1137805/slide-16.jpg)

















![Нули полиномов Чебышева Отрезок [–1,1] Отрезок [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1137805/slide-39.jpg)
 Зачем нужна математика
Зачем нужна математика Степень с отрицательным показателем
Степень с отрицательным показателем Презентация на тему Алгебра и начала математического анализа
Презентация на тему Алгебра и начала математического анализа  Презентация по математике "Переместительное свойство сложения" -
Презентация по математике "Переместительное свойство сложения" -  Погрешности измерений
Погрешности измерений Волшебная страна - Геометрия
Волшебная страна - Геометрия Линейная презентация
Линейная презентация Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Производная частного двух функций
Производная частного двух функций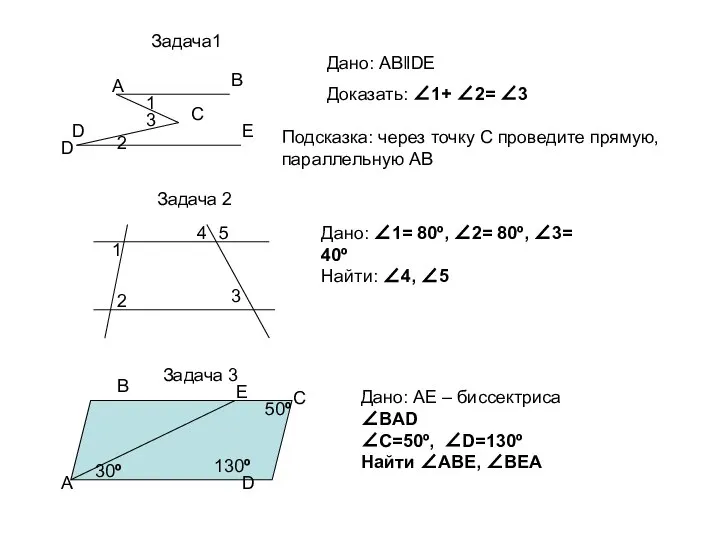 Параллельные прямые (тест)
Параллельные прямые (тест) MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia
MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia Пифагор и его школа
Пифагор и его школа 27.09 Графики функций
27.09 Графики функций Задачи на вычисление площадей и объемов тел вращения и многогранников
Задачи на вычисление площадей и объемов тел вращения и многогранников Декартова прямоугольная система координат на плоскости
Декартова прямоугольная система координат на плоскости Равенство углов наложением
Равенство углов наложением Самостоятельная работа по математике
Самостоятельная работа по математике Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс
Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс  Математическое путешествие (1 урок)
Математическое путешествие (1 урок) Тест для учащихся 1 класса
Тест для учащихся 1 класса Задачи на вычисление площади боковой поверхности циллиндра
Задачи на вычисление площади боковой поверхности циллиндра Форматы вывода результата вычислений и логические операции в MATLAB
Форматы вывода результата вычислений и логические операции в MATLAB Презентация на тему Куб
Презентация на тему Куб  Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Решение уравнений на нахождение слагаемого
Решение уравнений на нахождение слагаемого Повторение курса алгебры (7 класс)
Повторение курса алгебры (7 класс) Теорема Пифагора
Теорема Пифагора Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми