Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности

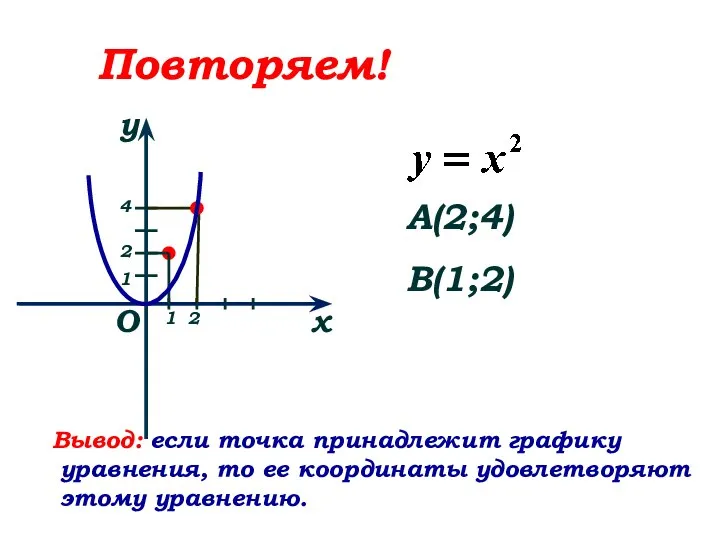
Повторяем!
O
x
y
A(2;4)
1
1
2
2
4
B(1;2)
Вывод: если точка принадлежит графику
уравнения, то ее координаты удовлетворяют
этому уравнению.

Алгебра:
По заданному уравнению линии исследовать
ее свойства.
Геометрия:
По геометрическим свойствам линии найти ее уравнение.

Задачи урока:
Узнать, что называется уравнением линии, окружности;
Понять, как по заданным свойствам окружности найти ее уравнение;
Научиться находить уравнение окружности.

УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ Х И У НАЗЫВАЕТСЯ УРАВНЕНИЕМ ЛИНИИ L, ЕСЛИ ЭТОМУ УРАВНЕНИЮ УДОВЛЕТВОРЯЮТ КООРДИНАТЫ ЛЮБОЙ ТОЧКИ ЛИНИИ L И НЕ УДОВЛЕТВОРЯЮТ КООРДИНАТЫ НИКАКОЙ ТОЧКИ, НЕ ЛЕЖАЩЕЙ НА ЭТОЙ ЛИНИИ.
Определение:

Уравнением фигуры Ф, заданной на плоскости xy, называют уравнение с двумя переменными x и y, имеющее такие свойства:
если точка принадлежит фигуре Ф, то ее координаты являются решением данного уравнения;
любое решение (x;y) данного уравнения является координатами точки, принадлежащей фигуре Ф.
Определение:

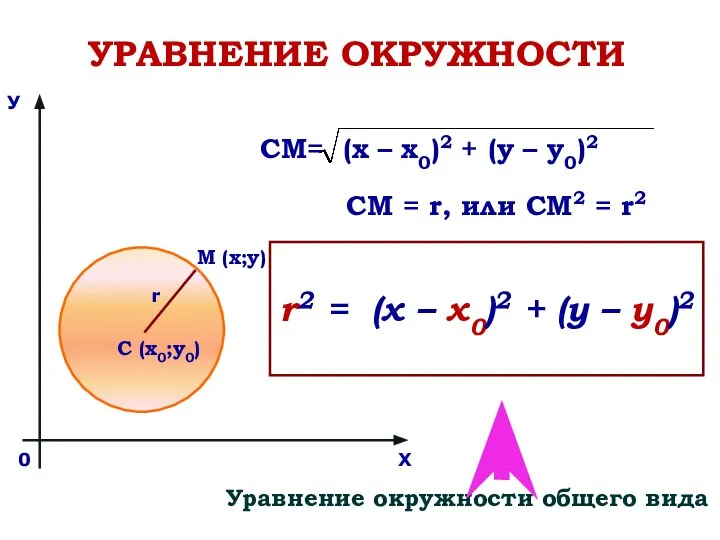
У
Х
0
М (х;у)
r
C (х0;у0)
УРАВНЕНИЕ ОКРУЖНОСТИ
СМ= (х – х0)2 + (у – у0)2
СМ = r, или СМ2 = r2
r2 = (х – х0)2 + (у – у0)2
Уравнение окружности общего вида

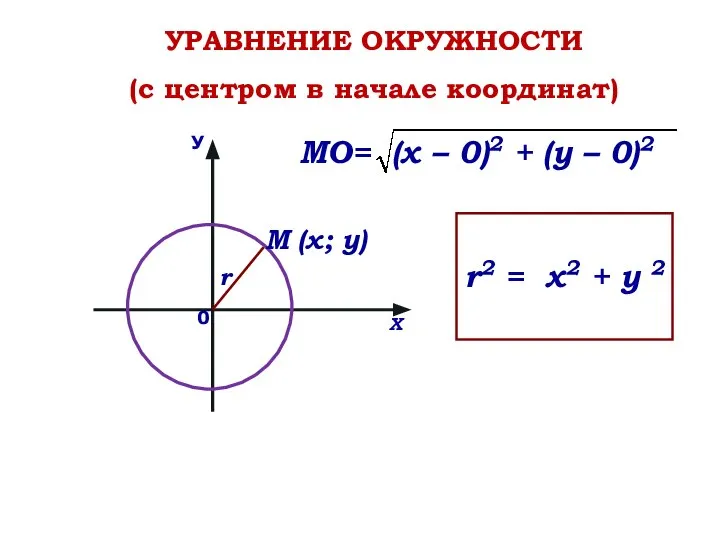
У
Х
0
М (х; у)
r
УРАВНЕНИЕ ОКРУЖНОСТИ
(с центром в начале координат)
МО= (х – 0)2 + (у – 0)2
r2 = х2 + у 2

Как составить уравнение окружности:
- узнать координаты центра;
- узнать длину радиуса;
подставить координаты центра и
длину радиуса в уравнение окружности
общего вида.

Например:
1. Центр С (2;4), радиус r = 3;
уравнение окружности:
(х – 2)2 + (у – 4)2 = 9
2. Центр С (0;0), радиус r = 4;
уравнение окружности:
х2 + у2 = 16

Решить задачи:
Окружность задана уравнением:
. Укажите координаты центра окружности и ее радиус.