Содержание
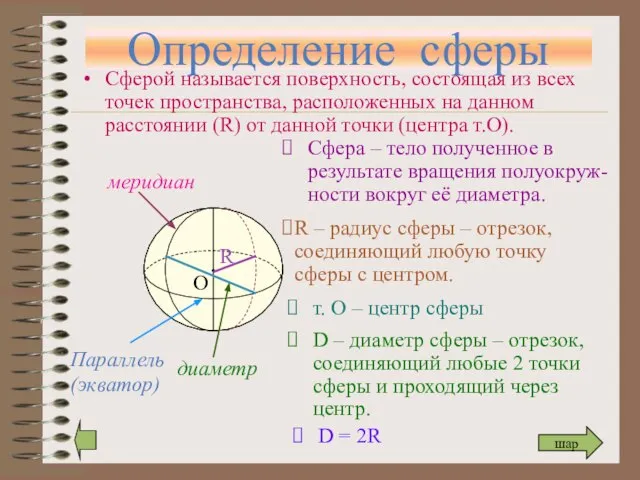
- 2. Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от
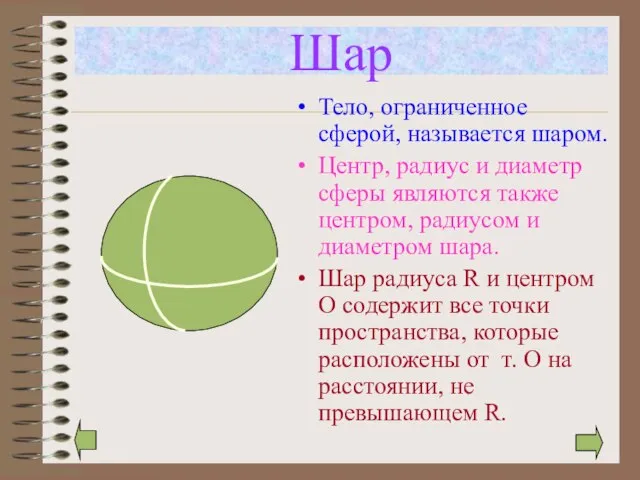
- 3. Шар Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы являются также центром, радиусом и
- 4. Уравнение окружности С(х0;у0) М(х;у) х у О следовательно уравнение окружности имеет вид: (x – x0)2 +
- 5. Задача 1. Зная координаты центра С(2;-3;0), и радиус сферы R=5, записать уравнение сферы. Решение так, как
- 6. Уравнение сферы (x – x0)2 + (y – y0)2 + (z – z0)2 = R2 х
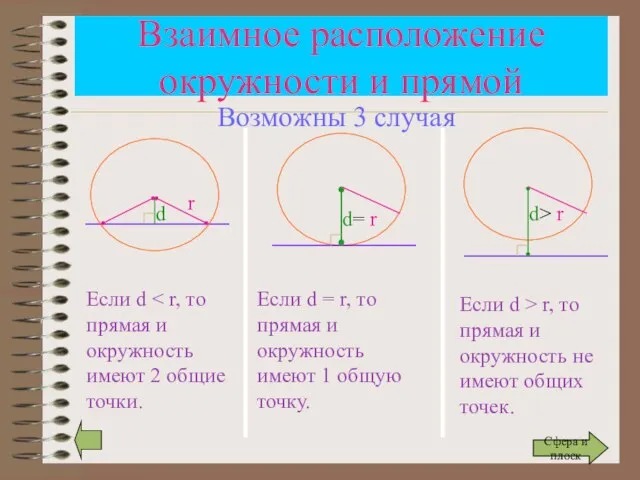
- 7. Взаимное расположение окружности и прямой r d Если d d= r d> r Если d =
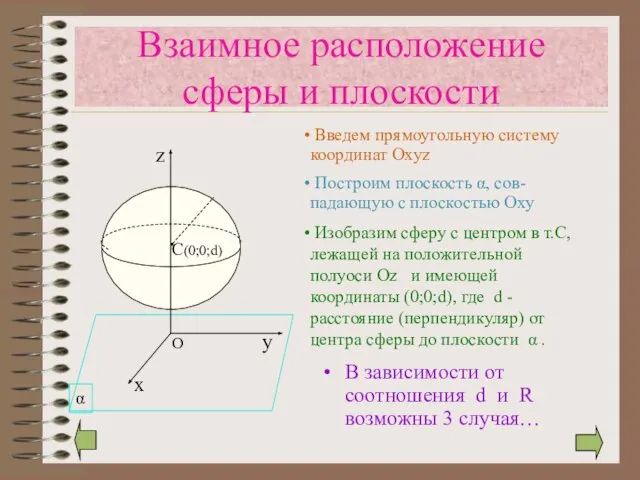
- 8. Взаимное расположение сферы и плоскости В зависимости от соотношения d и R возможны 3 случая… Введем
- 9. Сечение шара плоскостью есть круг. r Взаимное расположение сферы и плоскости Рассмотрим 1 случай d r
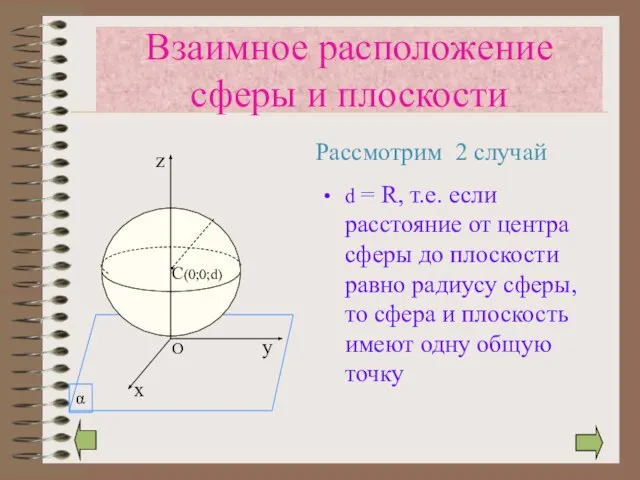
- 10. d = R, т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера
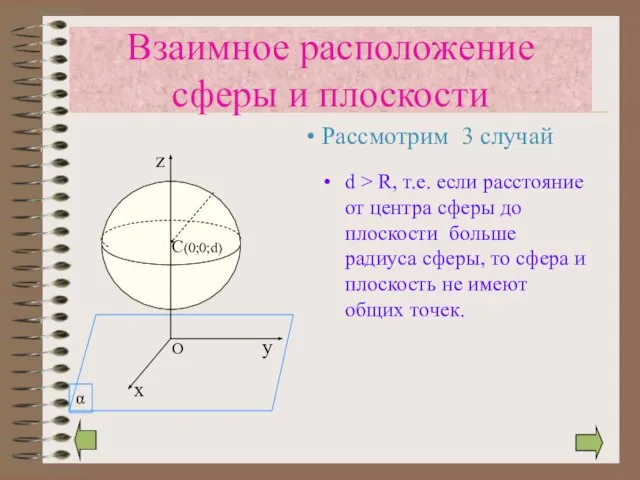
- 11. d > R, т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера
- 12. Задача 2. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти
- 14. Скачать презентацию





 Презентация на тему Квадратные уравнения 8 класс
Презентация на тему Квадратные уравнения 8 класс  Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1)
Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1) Прямые измерения, косвенные, совокупные и совместные
Прямые измерения, косвенные, совокупные и совместные 9
9 Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение)
Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение) Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной
Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Презентация на тему Простые и составные числа
Презентация на тему Простые и составные числа  Площадь треугольника
Площадь треугольника 6. СЛАУ. Методы решения (1)
6. СЛАУ. Методы решения (1) Операции над матрицами
Операции над матрицами Устный счет
Устный счет Числа-гиганты. Из истории чисел - гигантов
Числа-гиганты. Из истории чисел - гигантов Степенная функция
Степенная функция Логарифмы. Задание
Логарифмы. Задание Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Действие с дробями. Устная работа
Действие с дробями. Устная работа П 3
П 3 Игра - путешествие В стране занимательной математики
Игра - путешествие В стране занимательной математики Матрицы и действия над ними
Матрицы и действия над ними Презентация на тему Цилиндр (11 класс)
Презентация на тему Цилиндр (11 класс)  Векторы. Задачи
Векторы. Задачи Тема: Письменное умножение на двузначное число. Закрепление.
Тема: Письменное умножение на двузначное число. Закрепление.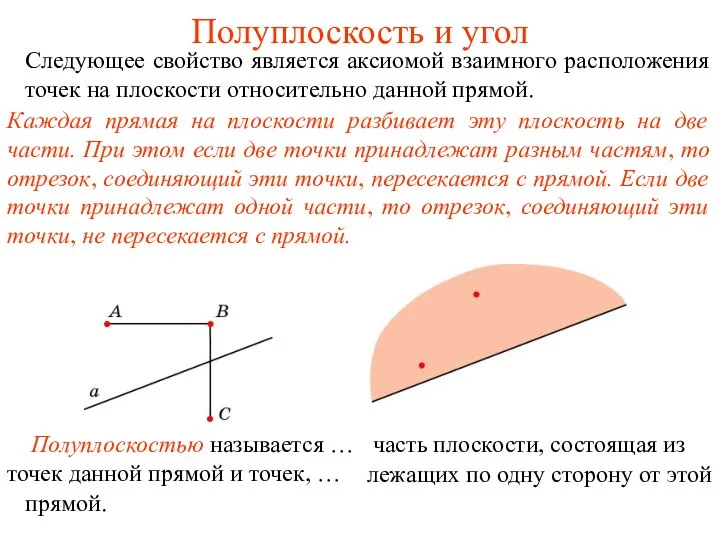 Полуплоскость и угол
Полуплоскость и угол Параллельные прямые (тест)
Параллельные прямые (тест)