Содержание
- 2. Алгоритм решения уравнений вида |f(х)|=|g(х)| Решения уравнения |f(х)|=|g(х)| равносильно решению двух уравнений: f(х)=g(х) или f(х)=-g(х)
- 3. Например: |5х-4|=|3х+2|; 5х-4=3х+2 или 5х-4=-3х-2; 2х=6 или 8х=2; Х=3 или х=0,25. Ответ: 0,25; 3.
- 4. 2. | х2 –3 х|=|х-3|; х2 –3 х=х-3 или х2 –3 х=-х+3; х2 -4х+3=0 или х2
- 5. Первый алгоритм решения уравнений вида |f(х)|=g(х) Уравнение |f(х)|=g(х) равносильно решению двух систем: 1) g(х)≥0, f(х)=g(х); 2)
- 6. Например: 1. |х+2|=2(3-х). или 3-х≥0, х+2=2(3-х); х≤3, х+2=6-2х; х≤3, 3х=4; х≤3, х=1⅓. х=1⅓. Ответ: х=1⅓. 3-х≥0,
- 7. 2. | х2 +х-3|=х или х≥0, х2 +х-3=х; х≥0, х2 -3=0; х≥0, х2 =3; х≥0, х=±√3;
- 9. Скачать презентацию






 Из истории теоремы Пифагора
Из истории теоремы Пифагора Векторы плоскости
Векторы плоскости Работа на повторение материала 6 класса
Работа на повторение материала 6 класса Тригонометрия тригонометрические функции
Тригонометрия тригонометрические функции Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Построение треугольника с помощью циркуля и транспортира
Построение треугольника с помощью циркуля и транспортира Кривые второго порядка. Практика
Кривые второго порядка. Практика Векторы. 9 класс
Векторы. 9 класс Подсчёт вероятности
Подсчёт вероятности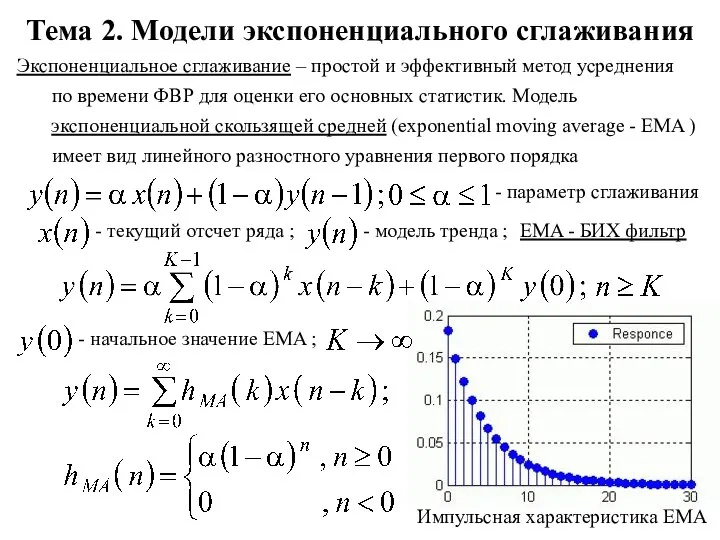 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Нахождение дроби от числа
Нахождение дроби от числа Построение сечений
Построение сечений Расстояние от точки до прямой
Расстояние от точки до прямой Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А.
Работу выполнила: Ученица 5б класса Беляева Александра Учитель: Сахокия Д.А. Упростите выражение
Упростите выражение Презентация на тему Логарифмические уравнения
Презентация на тему Логарифмические уравнения  Признаки равенства прямоугольных теугольников
Признаки равенства прямоугольных теугольников Преобразование графика квадратичной функции
Преобразование графика квадратичной функции Геометрические фигуры
Геометрические фигуры Степінь з цілим показником
Степінь з цілим показником Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Метод группировки
Метод группировки Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Равенство треугольников
Равенство треугольников Правильные многогранники
Правильные многогранники Статистические показатели
Статистические показатели Решение уравнений
Решение уравнений delenie_s_ostatkom-_2_
delenie_s_ostatkom-_2_