ВКР: Исследование динамики итерирования полиномов второй степени и кусочно-линейных функций

Актуальность
В настоящее время нелинейная динамика интенсивно развивается и находит приложение в разных отраслях знаний от лингвистики до нанотехнологий. В настоящей работе рассматривается два семейства нелинейных функций, порождаемых квадратным двучленом и тентообразной функцией.

Цель, объект и предмет исследования
Цель – исследование динамики итерирования логистической и тентообразной функций.
Объект исследования – нелинейная динамика.
Предмет исследования – сравнение динамик итерированных логистической и тентообразных функций.

Новизна
Адаптированы алгоритмы вычисления константы Фейгенбаума для логистической функции и тентообразной функции
Выявлена связь между кусочно-линейной функцией и множеством Кантора
Разботано многоэтапное математико-информационное задание

Задачи исследования
Задачи исследования:
Исследование орбит точек логистической и тентообразной функций
Разработать алгоритм и написать программу итерирования, вычисления констант Фейгенбаума, для логистической и тентообразной функций различных средах
Разработать многоэтапное математико-информационное задание

Практическая значимость
Практическая значимость работы заключается в том, что результаты исследования могут быть использованы при изучениях нелинейных отображений и построения математических моделей.

Переход к хаосу логистической функции
На данном этапе был подробно разобран переход к хаосу логистической функции. В нем было выяснено, что при увеличении значения a будет происходить бифуркация в орбиту длиной периода 2. Тем самым мы увидим удвоение периода у данной функции.

Символическая динамика логистической функции
На данном этапе было разобрано понятие символической динамики.
Из чего стало понятно, что это полезный метод для понимания куда попадет следующая точка xn+1 после выполнения итераций: слева от максимума (центра) (L), или справа от максимума (R), либо в максимум функции (C), где под максимумом понимается глобальный максимум функции f(x)=a(1-x)x на отрезке [0;1].

Вычисление констант Фейгенбаума
На данном этапе был разработан алгоритм и написана программа итерирования, вычисления констант Фейгенбаума, для логистической функции.

Построение множества Кантора для тентообразной функции
На данном этапе был построен алгоритм фрактальных множеств тентообразной функции f(x), каждое из которых является множеством Кантора. Алгоритм был реализован в среде MathCad.
Суть данного алгоритма в том, что рассматривается точка x и ее сотая итерация . Если то мы закрашиваем x в синий цвет и рассматриваем другую точку x+h. Множество закрашенное в синий цвет и даст нам множество Кантора.

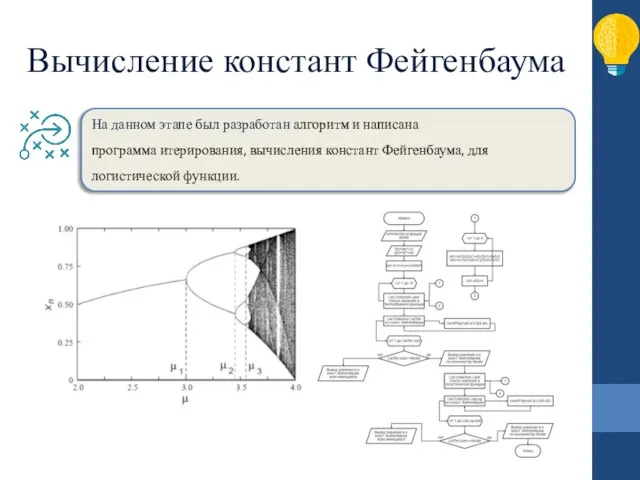
Вычисление констант Фейгенбаума
На данном этапе был разработан алгоритм и написана программа итерирования, вычисления констант Фейгенбаума, для тентообразной функции.